Effective mass in semiconductors
Contents - Glossary - Study Aids - 1 2 3 4 5 6 7 8 9
In this section:
- Introduction
- Energy-wavenumber
(E-k) diagram of silicon
- Detailed
parameters for Ge, Si and GaAs
- Density of
states mass
- Conductivity
mass
- Short
list of parameters for Ge, Si and GaAs
Introduction
The effective mass of a semiconductor is
obtained by fitting the actual E-k diagram around the conduction band
minimum or the valence band maximum by a parabola. While this concept is simple
enough the issue turns out to be substancially more complex due to the multitude
and the occasional anisotropy of the minima and maxima. In this section we first
describe the different relevant band minima and maxima, present the numeric
values for germanium, silicon and gallium arsenide and introduce the effective
mass for density of states calculations and the effective mass for conductivity
calculations.
Most semiconductors can be described as having one band minimum at k =
0 as well as several equivalent anisotropic band minima at k ¹ 0. In addition there are three band maxima of interest
which are close to the valence band edge.
As an example we consider the
band structure of silicon as shown in the figure below:
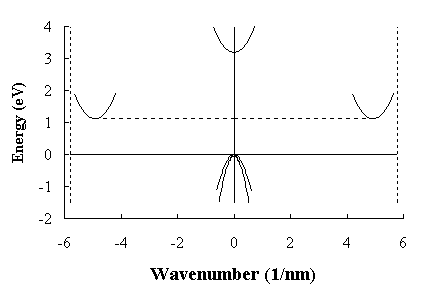 Shown is
the E-k diagram within the first brillouin zone and along the (100)
direction. The energy is chosen to be to zero at the edge of the valence band.
The lowest band minimum at k = 0 and still above the valence band edge
occurs at Ec,direct = 3.2 eV. This is not the lowest minimum
above the valence band edge since there are also 6 equivalent minima at k
= (x,0,0), (-x,0,0), (0,x,0), (0,-x,0), (0,0,x), and (0,0,-x) with x = 5
nm-1. The minimum energy of all these minima equals 1.12 eV =
Ec,indirect. The effective mass of these anisotropic minima is
characterized by a longitudinal mass along the corresponding equivalent (100)
direction and two transverse masses in the plane perpendicular to the
longitudinal direction. In silicon the longitudinal electron mass is
me,l* = 0.98 m0 and the
transverse electron masses are me,t* = 0.19
m0, where m0 = 9.11 x 10-31 kg is
the free electron rest mass.
Shown is
the E-k diagram within the first brillouin zone and along the (100)
direction. The energy is chosen to be to zero at the edge of the valence band.
The lowest band minimum at k = 0 and still above the valence band edge
occurs at Ec,direct = 3.2 eV. This is not the lowest minimum
above the valence band edge since there are also 6 equivalent minima at k
= (x,0,0), (-x,0,0), (0,x,0), (0,-x,0), (0,0,x), and (0,0,-x) with x = 5
nm-1. The minimum energy of all these minima equals 1.12 eV =
Ec,indirect. The effective mass of these anisotropic minima is
characterized by a longitudinal mass along the corresponding equivalent (100)
direction and two transverse masses in the plane perpendicular to the
longitudinal direction. In silicon the longitudinal electron mass is
me,l* = 0.98 m0 and the
transverse electron masses are me,t* = 0.19
m0, where m0 = 9.11 x 10-31 kg is
the free electron rest mass.
Two of the three band maxima occur at 0 eV. These bands are refered to as the
light and heavy hole bands with a light hole mass of
mlh* = 0.16 m0 and a heavy hole
mass of mhh* = 0.46 m0. In
addition there is a split-off hole band with its maximum at
Ev,so = -0.044 eV and a split-off hole mass of
mv,so* = 0.29 m0.
Effective mass and energy band minima and maxima of Ge, Si
and GaAs
The values of the energy band minima and maxima as well as the
effective masses for germanium, silicon and gallium arsenide are listed in the
table below:
| Name |
Symbol |
Germanium |
Silicon |
Gallium Arsenide |
| Band minimum at k = 0 |
|
|
|
|
| Minimum energy |
Eg,direct [eV] |
0.8 |
3.2 |
1.424 |
| Effective mass |
me*/m0 |
0.041 |
?0.2? |
0.067 |
| Band minimum not at k = 0 |
|
|
|
|
| Minimum energy |
Eg,indirect [eV] |
0.66 |
1.12 |
1.734 |
| Longitudinal effective mass |
me,l*/m0 |
1.64 |
0.98 |
1.98 |
| Transverse effective mass |
me,t*/m0 |
0.082 |
0.19 |
0.37 |
| Wavenumber at minimum |
k [1/nm] |
xxx |
xxx |
xxx |
| Longitudinal direction |
|
(111) |
(100) |
(111) |
| Heavy hole valence band maximum at E = k = 0 |
|
|
|
|
| Effective mass |
mhh*/m0 |
0.28 |
0.49 |
0.45 |
| Light hole valence band maximum at k = 0 |
|
|
|
|
| Effective mass |
mlh*/m0 |
0.044 |
0.16 |
0.082 |
| Split-off hole valence band maximum at k = 0 |
|
|
|
|
| Split-off band valence band energy |
Ev,so [eV] |
-0.028 |
-0.044 |
-0.34 |
| Effective mass |
mh,so*/m0 |
0.084 |
0.29 |
0.154 |
m0 = 9.11 x 10-31 kg is the free electron
rest mass.
Effective mass for density of states
calculations
The effective mass for density of states calculations equals
the mass which provides the density of states using the expression for one
isotropic maximum or minimum or:
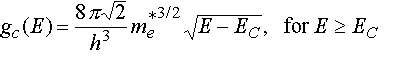 (f24a)
(f24a)
for the
density of states in the conduction band and:
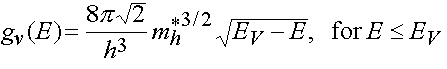 (24b)
(24b)
for the
density of states in the valence band.
for instance for a single band minimum described by a longitudinal mass and
two transverse masses the effective mass for density of states calculations is
the geometric mean of the three masses. Including the fact that there are
several equivalent minima at the same energy one obtains the effective mass for
density of states calculations from:
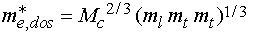 (f65)
(f65)
where Mc is the number of equivalent band minima. For
silicon one obtains:
me,dos* = (ml mt
mt)1/3 = (6)2/3 (0.89 x 0.19 x
0.19)1/3 m0 = 1.08 m0.
Effective mass for conductivity calculations
The
effective mass for conductivity calculation is the mass which is used in
conduction related problems accounting for the detailed structure of the
semiconductor. These calculations include mobility and diffusion constants
calculations. Another example is the calculation of the shallow impurity levels
using a hydrogen-like model.
As the conductivity of a material is inversionally proportional to the
effective masses, one finds that the conductivity due to multiple band maxima or
minima is proportional to the sum of the inverse of the individual masses,
multiplied by the density of carriers in each band, as each maximum or minimum
adds to the overall conductivity. For anisotropic minima containing one
longitudinal and two transverse effective masses one has to sum over the
effective masses in the different minima along the equivalent directions. The
resulting effective mass for bands which have ellipsoidal constant energy
surfaces is given by:
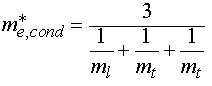 (f66)
(f66)
provided the material has an isotropic conductivity as is the case for cubic
materials. For instance electrons in the X minima of silicon have an
effective conductivity mass given by:
me,cond* = 3 x (1/ml +
1/mt + 1/mt)-1 = 3 x (1/0.89 + 1/0.19
+1/0.19)-1 m0 = 0.26 m0.
Effective mass and energy bandgap of Ge, Si and GaAs
| Name |
Symbol |
Germanium |
Silicon |
Gallium Arsenide |
| Smallest energy bandgap at 300 K |
Eg (eV) |
0.66 |
1.12 |
1.424 |
| Effective mass for density of states calculations |
|
|
|
|
| Electrons |
me*,dos/m0 |
0.56 |
1.08 |
0.067 |
| Holes |
mh*,dos/m0 |
0.29 |
0.57/0.811 |
0.47 |
| Effective mass for conductivity calculations |
|
|
|
|
| Electrons |
me*,cond/m0 |
0.12 |
0.26 |
0.067 |
| Holes |
mh*,cond/m0 |
0.21 |
0.36/0.3861 |
0.34 |
m0 = 9.11 x 10-31 kg is the free electron
rest mass.
1 Due to the fact that the heavy hole band does
not have a spherical symmetry there is a discrepancy between the actual
effective mass for density of states and conductivity calculations (number on
the right) and the calculated value (number on the left) which is based on
spherical constant-energy surfaces. The actual constant-energy surfaces in the
heavy hole band are "warped", resembling a cube with rounded corners and
dented-in faces.
© Bart J. Van Zeghbroeck, 1997