

Detta avsnitt handlar om olika metoder för att bevisa påståenden, och hur man kan konstruera ett bevis. I varje avsnitt finns en allmän beskrivning av metoden, varför den fungerar och minst ett exempel (med kommentarer i vänstra kolumnen och själva beviset i högra kolumnen). Observera att ett bevis ofta använder flera olika metoder. Innan vi börjar med bevis vill jag igen betona att definitionerna är viktiga.
Som sagt, definitionerna är viktiga eftersom ord kan ha en annan betydelse i matematiska sammanhang än i det vanliga språket. Vi vet att 2, 4, 6 och 8 är jämna tal, men dessa exempel på jämna tal hjälper oss inte att bevisa någonting om ett allmänt jämnt tal. Vi förstår vad ett jämnt tal är, men vi behöver också en exakt definition. Förståelse av vad vi jobbar med är naturligtvis viktigt, men definitionen behövs också så att vi kan jobba med idén, och bevisa påståenden.
När du läser en definition bör du kontrollera att den är vettig, och
försöka få en idé om vad den egentligen betyder. Betrakta följande
exempel.
En oflyttbar påle definieras som en påle som inte kan flyttas, och en ostoppbar kanonkula definieras som en kanonkula som inte kan stoppas.
 Vad händer om en ostoppbar
kanonkula träffar en oflyttbar påle?
Vad händer om en ostoppbar
kanonkula träffar en oflyttbar påle?
Direkt bevis är den mest rättframma varianten av bevis, och är en del av nästan alla andra bevismetoder.
| Att bevisa | p  q q |
| Metod | Anta att p är sant och skriv om det till q genom en sekvens av logiska steg. |
| Förklaring | Kom ihåg att p  q är
sant utom i fall där p är sant och q är falskt. Om vi börjar med p och
då får q, så vet vi att fallet där ''p är sant och q är falskt'' inte
uppstår. Det betyder att ''p q är
sant utom i fall där p är sant och q är falskt. Om vi börjar med p och
då får q, så vet vi att fallet där ''p är sant och q är falskt'' inte
uppstår. Det betyder att ''p  q'' är sant för alla sanningsvärden på p och q. q'' är sant för alla sanningsvärden på p och q. |
Nu försöker vi att bevisa att när man kvadrerar ett jämnt tal, får man ett jämnt tal. Under bevisets gång skriver jag kommentarer om tanken bakom varje steg. Det är för att försöka visa hur bevisprocessen fungerar, istället för att låta beviset som genom magi uppenbara sig på sidan.
| Sats | |
|---|---|
| När man kvadrerar ett jämnt tal får man ett jämnt tal. | |
| Kommentar | Bevis |
| Först måste vi analysera påståendet "När man kvadrerar ett jämnt tal får man ett jämnt tal" så att det blir lättare att hantera. Vi skriver det på formen "om p så q", och introducerar lite notation: "Om x är ett jämnt tal, så är x2 ett jämnt tal." | Vi skriver om påståendet till: "om x är ett jämnt tal, så är x2 ett jämnt tal". |
| Metoden går ut på att vi antar att p är sant och ska bevisa att q är sant. | Anta att x är ett jämnt tal. Vi bevisar att även x2 är jämnt. |
| Nu vet vi att x är jämnt men vad betyder jämnt? Det är en bra idé att kontrollera att du kan definitionerna av alla tekniska termer i ett påstående innan du börjar med resonemanget. Ett heltal x är jämnt om det existerar ett heltal k så att x = 2k. Kanske hjälper det — vad händer om vi sätter x = 2k i x2? Vi får x2 = (2k)2 = 4k2. Vad är det vi vill ha? Jo, vi vill visa att x2 är jämt, dvs. lika med 2 gånger ett heltal. Om vi skriver om 4k2 får vi 2(2k2) som är 2 gånger ett heltal. Det ser ut som om det fungerar, så vi renskriver det. | Eftersom x är jämnt existerar det ett heltal k så att x = 2k. Vi kvadrerar x = 2k och får x2 = (2k)2 = 2(2k2). Detta är produkten av 2 och heltalet 2k2 så x2 är jämnt. |
Bevisa, med hjälp av direkt bevis, följande påståenden.
1. Om x och y är jämna, så är xy jämnt.
2. Låt a, b och c vara heltal. Om a | b och b | c, så
gäller a | c.
3. Om a och b har samma rest när de divideras med 5, så är
a – b delbart med 5.
4. För alla mängder A, B och C: om A 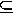 B och B
B och B 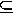 C, så gäller A
C, så gäller A 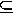 C.
C.
 Vad är fel i följande bevis?
Vad är fel i följande bevis?
Vi bevisar att om x är ett tal, så gäller
x2 – 5 + 1 = (x – 2)(x + 2).
Bevis:
x2 – 5 + 1 =
(x – 2)(x + 2)
x2 – 4 =
x2 – 2x + 2x – 4
x2 – 4 = x2 – 4
Eftersom den sista raden är sann, så är den första, dvs.
x2 – 5 + 1 =
(x – 2)(x + 2), sann.
Ofta är det lättare att bevisa att ett ekvivalent påstående är sant, än att bevisa att det ursprungliga påståendet är det. Kom ihåg att två påståenden är ekvivalenta om de har precis samma sanningsvärden. Bevis med hjälp av det kontrapositiva påståendet och motsägelsebevis (avsnitt 3.4) är två exempel på denna metod.
| Att bevisa | p  q q |
| Metod | Bevisa kontrapositiva påståendet "icke q  icke p"
(OBS: p och q har bytt sida!) icke p"
(OBS: p och q har bytt sida!) |
| Förklaring | p  q och icke q q och icke q  icke p är ekvivalenta (kolla
detta med hjälp av en sanningtabell!), så båda är sanna eller båda är
falska. icke p är ekvivalenta (kolla
detta med hjälp av en sanningtabell!), så båda är sanna eller båda är
falska. |
| Sats | |
|---|---|
| För alla heltal n gäller att om n2 är jämnt så är n jämnt. | |
| Kommentar | Bevis |
| Kanske är din första tanke att försöka med direkt bevis. Vi provar det. Anta att n2 är jämnt. Då kan vi skriva det som n2 = 2k. Nu gäller n = ± √(n2) = ± √(2k). Erm… vi har ingen aning om √(2k) är jämnt eller udda… Det gick inte så bra så vi provar någonting annat. Vi försöker med det kontrapositiva påståendet. Vad är det? Låt p vara påståendet ''n2 är jämnt'' och låt q vara ''n är jämnt''. Det kontrapositiva påståendet blir ''För alla heltal n gäller att om n inte är jämnt så är n2 inte jämnt''. Naturligtvis kan vi skriva om det till ''För alla heltal n gäller att om n är udda så är n2 udda''. | Låt n vara ett heltal. Vi bevisar det ekvivalenta påståendet, ''För alla heltal n gäller att om n är udda så är n2 udda''. |
| Problemet är nu ganska likt det i exempel 3.2.1 — kanske nästan samma bevis gäller om vi byter ut jämnt mot udda? Vad betyder ''n är udda''? Det betyder att det ger rest 1 när det divideras med 2. Hur skriver vi det? Om n är udda så existerar det ett heltal k så att n = 2k + 1. Kvadrering ger (2k + 1)2 = 4k2 + 4k + 1, som är 2 gånger ett heltal plus 1, alltså udda. | Anta att n är udda. Då existerar det heltal k så att n = 2k + 1. Vi sätter in n = 2k + 1 i n2 och får n2 = (2k + 1)2 = 2(2k2 + 2k) + 1, som är ett udda tal eftersom 2k2 + 2k är ett heltal. Detta bevisar att för alla heltal n gäller att om n är udda så är n2 udda, vilket också bevisar att för alla heltal n gäller att om n2 är jämnt, så är n jämnt. |
Bevisa följande påståenden med hjälp av motsvarande kontrapositiva påstående.
1. För varje heltal n gäller att om n2 är udda så är n udda.
2. För alla positiva heltal m och n gäller att om m + n är udda
så är precis ett av m och n udda.
3. För varje heltal n gäller att om n2 inte är delbart med 7 så
är n inte delbart med 7.
Ofta kan man använda motsägelsebevis i samma situation som bevis med hjälp av det kontrapositiva påståendet. Vilken metod bör man använda? Det är för det mesta en smaksak. Det finns ingen lätt och klar regel som säger ''i dessa fall är denna bevismetoden bäst'' — det kan man bara avgöra med hjälp av erfarenhet. Hur kan man få erfarenhet? Det finns två sätt: att läsa andras bevis eller att göra bevis själv. När man har läst många bevis och försöker att bevisa någonting nytt, är det ofta så att man tänker ''det påminner mig om beviset av…''; så man tittar på det beviset och använder metoder och knep som man har sett tidigare.
| Att bevisa | p  q q |
| Metod | Bevisa ''p och icke q'' är falskt. |
| Förklaring | ''p och icke q'' är negationen av ''p  q''. (Kolla detta med hjälp av en sanningstabell!)
Det betyder att om vi bevisar att ''p och icke q'' är falskt så är ''p q''. (Kolla detta med hjälp av en sanningstabell!)
Det betyder att om vi bevisar att ''p och icke q'' är falskt så är ''p
 q'' sant. q'' sant. |
| Sats | |
|---|---|
| Det finns ett oändligt antal primtal. | |
| Kommentar | Euklides Bevis |
Påståendet är inte på formen ''p  q'', så först måste vi bestämma precis vad som
är vad i påståendet. Vi kan skriva om det till ''om S är mängden
av alla primtal så är S oändlig''. Då är p = ''S är en
mängd primtal'' och q = ''S innehåller oändligt många
element''. För att göra ett motsägelsebevis antar vi att ''p och
icke q'' är sant, dvs. ''S är mängden av alla primtal och S är
ändlig'', och visar att detta leder till en motsägelse. q'', så först måste vi bestämma precis vad som
är vad i påståendet. Vi kan skriva om det till ''om S är mängden
av alla primtal så är S oändlig''. Då är p = ''S är en
mängd primtal'' och q = ''S innehåller oändligt många
element''. För att göra ett motsägelsebevis antar vi att ''p och
icke q'' är sant, dvs. ''S är mängden av alla primtal och S är
ändlig'', och visar att detta leder till en motsägelse. |
Anta att S är mängden av alla primtal och att S är ändlig. Då kan vi skriva upp elementen: S = {p1, p2,…, pk}. |
| Nästa steg är klurigt att komma på själv. Man multiplicerar alla primtal och adderar 1. Varför? För att det fungerar! | Låt n = p1p2…pk + 1. |
| Vi vet att varje positivt heltal större än 1 kan skrivas som en
produkt av positiva primtal. Vilka primtal i S är faktorer i n? Om vi
dividerar n med p1 blir resten 1, så p1 delar
inte n. Samma gäller för p2 osv. ...hmmm... S är mängden av alla primtal och det finns ett primtal som delar n, men det finns inte ett primtal i S som delar n. Det är nonsens, vi har alltså fått en motsägelse, och därför måste något av våra antaganden vara falskt. Det enda antagandet som kan vara falskt är att det finns ändligt många primtal. |
Eftersom n > 1 och n är ett heltal, så har n en faktor p som är ett primtal (aritmetikens fundamentalsats). Denna faktor p är inte någon av primtalen pi i S ty pi är inte faktor till n för i = 1,2,3,…k. Men vi antog att det inte fanns några andra primtal, så det är en motsägelse. Alltså måste S vara oändlig. |
Bevisa följande.
Ofta vill vi visa att två påståenden p och q är ekvivalenta, dvs. att de
har samma sanningsvärden. Vi säger ''p om och endast om q'' och skriver ''p
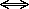 q''. Ett sätt att bevisa
''p
q''. Ett sätt att bevisa
''p 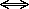 q'' är att dela upp det
i två delar och bevisa dem var för sig.
q'' är att dela upp det
i två delar och bevisa dem var för sig.
| Att bevisa | p 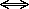 q q |
| Metod | Bevisa ''p  q'' och ''q q'' och ''q
 p''. Dem bevisar man med
hjälp av metoderna som vi har diskuterat tidigare: direkt bevis, bevis
med hjälp av det kontrapositiva påståendet eller motsägelsebevis. p''. Dem bevisar man med
hjälp av metoderna som vi har diskuterat tidigare: direkt bevis, bevis
med hjälp av det kontrapositiva påståendet eller motsägelsebevis. |
| Förklaring | ''p 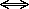 q'' är ekvivalent
med ''(p q'' är ekvivalent
med ''(p  q) och (q q) och (q  p)''. (Kolla detta med hjälp av en
sanningstabell!) p)''. (Kolla detta med hjälp av en
sanningstabell!) |
| Sats | |
|---|---|
| För alla heltal n gäller att n2 är jämnt om och endast om n är jämnt. | |
| Kommentar | Bevis |
| Först antar vi att n är ett heltal. Vi delar upp ''n2 är jämnt om och endast om n är jämnt'' i två påståenden: ''om n2 är jämnt så är n jämnt'' och ''om n är jämnt så är n2 jämnt''. Vi har redan bevisat båda påståendena så beviset är därmed klart! | Från satserna i Exempel 3.2.1 och 3.3.1 vet vi att ''för alla heltal n gäller att om n är jämnt så är n2 jämnt'' och ''För alla heltal n gäller att om n2 är jämnt så är n jämnt''. Tillsammans bevisar de att ''för alla heltal n är n2 jämnt om och endast om n är jämnt''. |
| Sats | |
|---|---|
Låt A, B och C vara mängder. Då gäller
(A  B) B)
 C
=(A C
=(A  C) C)
 (B
(B  C). C). |
|
| Kommentar | Bevis |
| Kanske undrar du hur detta påstående kan vara ''om och endast om''?
Vi kommer till det snart, men först måste vi se hur definitionerna av
mängdoperationerna ser ut. Definitionerna är: X = Y betyder att (x  X) X)
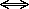 (x (x  Y).
Y). X  Y =
{x: x Y =
{x: x  X och x X och x  Y}. Y}.X  Y = {x: x Y = {x: x  X eller x X eller x  Y}.
Y}.Vad är det vi vill visa? Det är (A  B) B)  C = (A C = (A  C) C)  (B (B  C) C)som kan skrivas om till x  (A (A  B) B)  C C 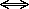 x  (A (A
 C) C)  (B (B  C). C).Vi ser att vi behöver dela upp beviset som i föregående exempel. Vi använder definitionerna och en del logik. |
Vi vill visa att x  (A (A  B) B)  C C 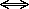 x x  (A (A
 C) C)  (B (B  C). C).Anta att x  (A (A  B) B)  C. Med hjälp av definitionen av snitt kan vi skriva om det
till x C. Med hjälp av definitionen av snitt kan vi skriva om det
till x  (A (A  B) och x B) och x  C. Definitionen
av union ger att detta är ekvivalent med (x C. Definitionen
av union ger att detta är ekvivalent med (x  A eller x A eller x  B) och x B) och x  C. Observera att vi måste behålla
paranteserna. Från logiken vet vi att ''(p eller q) och r'' är
ekvivalent med ''(p och r) eller (q och r)'', så C. Observera att vi måste behålla
paranteserna. Från logiken vet vi att ''(p eller q) och r'' är
ekvivalent med ''(p och r) eller (q och r)'', så''(x  A eller x A eller x  B) och x B) och x  C'' C''är ekvivalent med ''(x  A och x A och x  C) eller (x C) eller (x  B och x B och x  C)''. C)''.Med hjälp av definitioner igen, får vi nu att ''(x  A och x A och x  C) eller (x C) eller (x  B och x B och x  C)'' C)''är ekvivalent med ''x  (A (A  C) eller x C) eller x  (B (B  C)'' C)''som i sin tur är ekvivalent med ''x  (A (A  C) C)  (B (B C)''. C)''.Så ''x  (A (A  B) B)  C'' C''är ekvivalent med ''x  (A (A  C) C)  (B (B C)'', C)'',dvs. (A  B) B)  C = (A C = (A  C) C)  (B (B C). C). |
 B)
B)  C = (A
C = (A  C)
C)
 (B
(B  C).
C).
Ibland vill man visa att ett påstående är falskt, vilket innebär att man försöker hitta ett exempel för vilket det är falskt. Ett sådant exempel kallas för ett motexempel.
| Att bevisa | icke (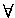 x,
p(x)) x,
p(x)) |
| Metod | Hitta ett x så att p(x) inte är sant |
| Förklaring | Om p(x) är falskt för något x så kan det inte vara sant för alla x,
så alltså måste 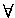 x, p(x) vara
falskt. x, p(x) vara
falskt. |
Bestäm om följande påståenden är sanna eller falska, och visa det genom att ge ett motexempel eller göra ett bevis.
| Påstående | Sant eller falskt? | Bevis eller motexempel |
|---|---|---|
| Alla i detta rum är levande. | Sant(?) | Kontrollera att ingen är död! |
| För alla heltal n gäller n2 ≤ 3n. | Sant | Det är enkelt att kontrollera att detta resultat är sant för små värden på n. Men vi kan inte kontrollera alla värden på n ett efter ett, eftersom de är oändligt många. Hur kan vi bevisa påståendet? Vi behöver en ny bevismetod, induktion, som vi diskuterar senare (i avsnitt 3.8). |
| Alla i hela världen har blont hår. | Falskt | Prinsessan Victoria har brunt hår. |
| För alla reella tal x gäller x2 ≥ x. | Falskt | Låt x = 1/2. Då är x2 = 1/4 < x. |
Bestäm om följande påståenden är sanna eller falska. Bevisa dem som är sanna och ge ett motexempel till dem som är falska.
 B| = |A| + |B| för alla mängder A
och B.
B| = |A| + |B| för alla mängder A
och B.
Det finns två grundläggande sätt att bevisa att något existerar, dvs. att
bevisa ett påstående av typen 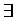 x: P(x). Det första sättet är att konstruera
ett exempel. För att göra detta ger vi ett exempel b och visar att P(b) är
sant.
x: P(x). Det första sättet är att konstruera
ett exempel. För att göra detta ger vi ett exempel b och visar att P(b) är
sant.
Det andra sättet är icke-konstruktivt. Det betyder att trots att vi inte
kan skriva upp hur exemplet ser ut så existerer ett sådant exempel. Alla
vet att någon mördade Olof Palme trots att vi inte säkert vet vem det var
som gjorde det. Vi vet att ''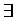 x: x mördade Olof Palme'' är sant, men
vi vet inte vem x är.
x: x mördade Olof Palme'' är sant, men
vi vet inte vem x är.
Vi börjar med konstruktionen av ett exempel.
| Att bevisa | 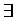 x: P(x) x: P(x) |
| Metod | Hitta ett x sådant att p(x) är sant |
| Förklaring | Påståendet behöver bara att ett exempel existerar, så att lägga fram ett exempel uppfyller påståendet och visar att det är sant. |
| Påstående | Sant eller falskt | Bevis |
|---|---|---|
| Det finns ett primtal mindre än 10. | Sant | 2 är mindre än 10 och det är ett primtal eftersom det inte är en enhet och de enda positiva delarna är 1 och 2 själv. |
| Storsjöodjuret existerar. | Sant? Falskt? |
Jag kan inte bevisa eller motbevisa detta. Jag kan inte hitta Storsjöodjuret och jag kan inte heller söka igenom hela Storsjön och visa att det inte finns där. |
| När man kvadrerar ett heltal kan man få noll. | Sant | Låt x = 0. Då är x2 = 02 = 0. |
Bevisa eller motbevisa dessa påståenden.
Ibland är det inte möjligt att skriva upp ett exempel för att fastställa existens. Förra vintern lämnade jag mitt hem iklädd min kappa, som hade alla knappar kvar. När jag kom fram till mitt arbete saknades en av knapparna. Jag kan säga att det existerar en punkt i tiden när knappen ramlade bort. Jag vet inte exakt när det hände, men det är utan tvekan så det hände. Följande exempel kan också illustrera ett icke-konstruktivt bevis.
| Sats | |
|---|---|
| Det finns två personer i Sverige som har samma antal hårstrån på sitt huvud. | |
| Kommentar | Bevis |
| Vi behöver ett idé att starta detta bevis med. Det ser inte ut att vara mycket information i frågan, så vi måste vända oss till vår egen erfarenhet. Vad vet vi om det som nämns i påståendet? Vad kan vi veta (eller kan vi gissa och kontrollera senare) om antalet hår på huvudet eller människor i Sverige som kan hjälpa oss? Hur många hår kan man ha på huvudet? Låt oss ta 2 miljoner hår som en övre gräns för ögonblicket och se om vi kan förfina det senare. | |
| Vi behöver också veta antalet människor i Sverige. Det är definitivt mer än 8 miljoner människor i Sverige. Alltså: 2 miljoner möjliga hårstrån på huvudet och 8 miljoner människor. Så högst 2 miljoner människor kan ha olika antal hårstrån på huvudet. Det verkar som vi kommer någonstans, kanske vi skulle försöka att skriva ner det korrekt. | Ingen person har mer än två miljoner hårstrån på sitt huvud. Det är minst åtta miljoner människor i Sverige. Anta att ingen av dessa åtta miljoner människor har samma antal hårstrån på huvudet. Då måste det finnas åtta miljoner olika positiva heltal som alla är mindre än eller lika med två miljoner. Men det finns bara två miljoner sådana heltal, nämligen 1, 2, 3,…, 2000000. |
| Nu har vi grunden för ett motsägelse. Vi måste ha åtta miljoner positiva heltal men vi har bara två miljoner. | Vi har en motsägelse, så vårt antagande att inte två personer har samma antal hårstrån på huvudet är falskt, vilket bevisar att det finns minst två människor med samma antal hårstrån på huvudet. |
Kan vi säga något mer än detta? Kan vi säga att minst 24 människor har samma antal hårstrån på huvudet? Eller åtminstone 4 eller något annat antal? Kan du bygga på argumentationen eller generalisera på något sätt?
Bevisa eller motbevisa dessa påståenden.
Tänk på en rad dominobrickor som är placerade så pass nära varandra, att om en dominobricka välter, så välter även nästa bricka. Om bricka 1 välter, så kommer den att välta bricka 2, som i sin tur välter bricka 3, och så vidare. Det vill säga, om bricka 1, 2, 3,…, k välter, så välter även bricka k + 1, och detta gäller för alla k ≥ 1.
Anta att vi vet följande. Vilken slutsats kan vi dra?
Det vi vet är: om processen med vältande dominobrickor börjar (bricka 1 välter) och om det gäller att om alla föregående brickor välter så välter också nästa bricka, så kan vi dra slutsatsen att alla brickor välter. Eller för att säga det på ett annat sätt: bricka n välter för alla positiva heltal n.
Vi kommer nu formalisera denna metod för att få den så kallade induktionsprincipen. Låt P(n) vara påståendet "dominobricka n välter". Vi skriver P(n) för att markera att dess sanningsvärde är beroende av n.
 P(k+1)'' är sant för alla heltal k ≥ 1.
P(k+1)'' är sant för alla heltal k ≥ 1.
Då är P(n) sant för alla heltal n ≥ 1.
Vi kunde startat med att välta dominobricka 5 och då skulle alla dominobrickor från och med nummer 5 också välta. Det kan generaliseras till följande.
Låt n0 vara ett heltal och antag att
 P(k+1)'' är sant för
alla heltal k ≥ n0
P(k+1)'' är sant för
alla heltal k ≥ n0
Då är P(n) sant för alla heltal n ≥ n0.
Med andra ord, så länge som vi har en startpunkt så spelar det ingen roll vad startpunkten är numrerad som.
Steg 1 kallas för induktionsbasen och steg 2 för induktionssteget.
| Sats | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Låt Sn vara summan av de första n positiva heltalen. Då är Sn = n(n + 1)/2, för alla heltal n ≥ 1. | ||||||||||||||||
| Kommentar | Bevis | |||||||||||||||
| Vi börjar med att ange vad vi kommer att bevisa. | Låt P(n) vara påståendet Sn = n(n + 1)/2. Vi kommer att bevisa att P(n) är sant för alla heltal n ≥ 1. | |||||||||||||||
| Nu kan vi bevisa induktionsbasen. Här har vi n = 1 som våran induktionsbas så vi vill bevisa att P(1) är sant. Vad är S1? Det är summan av de första ''1'' positiva heltalen, vilket är 1. | I. Induktionsbas Låt n = 1. Då är S1 = 1, och n(n + 1)/2 = 1(1 + 1)/2 = 1, dvs. Sn = n(n + 1)/2 vilket bevisar P(1). |
|||||||||||||||
| Nu när vi bevisat induktionsbasen, kommer vi att bevisa att om P(1), P(2),…, P(k) är sanna för något heltal k ≥ 1 så är P(k+1) också sant. Tänk tillbaka på, att för att bevisa "om p så q" påståendet så behöver vi bara titta på de fall där p är sant. (Se avsnitt 3.2 om direkt bevis.) Vi antar att p är sant och försöker att resonera logiskt tills vi når fram till q. Eftersom vi har börjat med något som är sant, och argumenterar korrekt, så vet vi att q är sant. | II. Induktionssteg Vi vill nu bevisa att "om P(1) och P(2) och … och P(k) är sanna för något k ≥ 1 så är P(k+1) sant". Vi antar därför att P(1) och P(2) och … och P(k) är sanna, för något k ≥ 1. T.ex. så är P(k) ekvivalent med Sk = k(k + 1)/2. Vi visar att P(k+1), som är ekvivalent med Sk+1 = (k + 1)(k + 2)/2, är sant. |
|||||||||||||||
| Vad vi nu gör är att betrakta Sk+1 vilket är summan av de första k + 1 heltalen, och sedan använder vi att P(k) är sant för att bevisa att Sk+1 är lika med (k + 1)(k + 2)/2. Kom ihåg att din argumentation skall vara enkel att följa, och att det skall vara förståeligt av människor som inte har tänkt på det här problemet själva. | Betrakta Sk+1.
Detta bevisar att P(k+1) är sant ifall P(1), P(2),…, och P(k) är sanna. |
|||||||||||||||
Nu när vi har slutfört beviset av både P(1) och
''P(1) och … och P(k)  P(k+1)'' behöver vi bara dra
slutsatsen att vi har bevisat påståendet. Utan denna slutsats är beviset
inte komplett. P(k+1)'' behöver vi bara dra
slutsatsen att vi har bevisat påståendet. Utan denna slutsats är beviset
inte komplett. |
III. Slutsats Vi har nu bevisat genom induktionbevis att P(1) är sant och ''P(1) och … och P(k)  P(k+1) för
k ≥ 1'' är sant, så vi har bevisat att P(n) är sant
för alla heltal n ≥ 1. P(k+1) för
k ≥ 1'' är sant, så vi har bevisat att P(n) är sant
för alla heltal n ≥ 1. |
|||||||||||||||
Det är inte bara exempel som resultat om summan ovan som vi kan bevisa med hjälp av induktion. Vi kan också bevisa resultat om t.ex. delbarhet, eller som inte har med aritmetik att göra över huvud taget (se Johnsonbaugh Edition 5 s. 44 - 45 (50 - 51 i Edition 4) [57 - 58 i Edition 6]).
| Sats | |
|---|---|
| För alla positiva heltal n är n2 + n delbart med 2. | |
| Kommentar | Bevis (Induktion över n) |
| Denna gång skriver vi ett bevis utan att använda notationen P(n). Denna notation är sällan använd, även om det till en början hjälper för att klargöra vad vi gör. | I. Induktionsbas Låt n = 1, då är n2 + n = 12 + 1 = 2, vilket definitivt är delbart med 2. Detta bevisar att påståendet är sant för n = 1. |
| Nu när vi har bevisat induktionsbasen, kommer vi att bevisa nästa steg. Vad betyder delbart? Det betyder att resten är 0. | II. Induktionssteg Anta att påståendet är sant för n = 1, 2 , … , k där k ≥ 1. För n = k medför det, att k2 + k är delbart med 2. Vi vill bevisa att påståendet är sant för n = k + 1, dvs. att (k + 1)2 + (k + 1) är delbart med 2. |
| För att visa att ett heltal är delbart med 2 kan vi försöka skriva det som att 2 gånger ett heltal (definitionen), eller vi kan skriva det som summan av jämna heltal. Förvissa dig om att du kan bevisa att summan av två jämna heltal är jämnt (Sats B3.1 i Block 3). Kom ihåg att vi har antagit att k2 + k är delbart med 2. | Betrakta (k + 1)2 + (k + 1). Vi kan skriva om detta som (k + 1)2 + (k + 1) = k2 + 2k + 1 + k + 1 = k2 + 3k + 2. |
| Vi har antagit att k2 + k är delbart med 2, så vi tar ut det och ser vad vi har kvar. | Nu har vi k2 + 3k + 2 = (k2 + k) + 2(k + 1). Från vårt antagande är k2 + k delbart med 2. Nästa term, 2(k + 1) där (k + 1) är ett heltal, är också delbart med 2. Eftersom summan av två jämna heltal alltid är jämnt måste också (k2 + k) + 2(k + 1) vara jämnt, och därför delbart med 2. Men detta var ju samma sak som (k + 1)2 + (k + 1). Vi har alltså visat att påståendet är sant för n = k + 1. |
| Och nu till slutsatsen. | III. Slutsats Eftersom (i) påståendet är sant för n = 1 och (ii) om det är sant för n = 1,…,k, så är det också sant för n = k + 1, så har vi med hjälp av induktion visat att det är sant för alla positiva heltal n. |
| Sats | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2n ≥ n2 för alla heltal n ≥ 4. | |||||||||||||||||||||||||||||||||
| Kommentar | Bevis | ||||||||||||||||||||||||||||||||
| Observera att vi börjar med n = 4. | I. Induktionsbas Låt n = 4, då är 2n = 24 = 16 och n2 = 42 = 16 så 2n ≥ n2 för n = 4. |
||||||||||||||||||||||||||||||||
Nu måste vi bevisa att P(1),…,P(k)  P(k+1). Vi behöver bevisa det med hjälp av ett direkt
bevis. Glöm inte att med ett direkt bevis antar man att
P(1),…,P(k) är sanna och visar att P(k+1) är sant. Glöm inte
heller att ange k ≥ 4. Det behöver vi i beviset! P(k+1). Vi behöver bevisa det med hjälp av ett direkt
bevis. Glöm inte att med ett direkt bevis antar man att
P(1),…,P(k) är sanna och visar att P(k+1) är sant. Glöm inte
heller att ange k ≥ 4. Det behöver vi i beviset! |
II. Induktionsteg Anta att 2k ≥ k2 för ett heltal k ≥ 4. (Induktionsantagande) Vi vill visa att 2(k + 1) ≥ (k + 1)2. |
||||||||||||||||||||||||||||||||
| Nu måste vi, med hjälp av 2k ≥ k2, visa att 2(k + 1) ≥ (k + 1)2. Det kan vara lite svårt att se precis vad det är vi vill komma fram till, så vi skriver om (k + 1)2 som k2 + 2k + 1, och jämför hela tiden med detta. | |||||||||||||||||||||||||||||||||
| Vi har 2k+1. Hur kan vi skriva om det så att vi kan
använda 2k ≥ k2? Jo,
2k+1 = 2·2k så
2·2k > 2·k2
(multiplikation av
båda sidorna av 2k ≥ k2 med 2.) Vi jämför 2k2 med k2 + 2k + 1 och ser att vi har k2 i båda. 2k2 = k2 + k2 så vad vi har kvar att jämföra är k2 och 2k + 1. Vi vet att k ≥ 4, så k·k ≥ 4·k, dvs. k2 ≥ 4k. På samma sätt är 4k ≥ 8. | Betrakta 2k+1:
|
||||||||||||||||||||||||||||||||
| Kom ihåg slutsatsen! | III. Slutsats Med hjälp av induktion har vi visat att 2n ≥ n2 för alla heltal n ≥ 4. |
||||||||||||||||||||||||||||||||
Varför började vi med n = 4 i föregånde bevis? Om n = 1, gäller 21 ≥ 12, så vad skulle har hänt om vi hade börjat med n = 1? Induktionsbasen skulle fungera, men induktionssteget går inte:
| 2k+1 | = | 2k2 | OK |
| ≥ | 2k2 | (induktionsantagandet), OK | |
| ≥ | k2 + k2 | OK | |
| ≥ | k2 + 4k | (ty k ≥ 4) Vi måste byta ut 4 mot 1, och då är det kört eftersom k2 + 1·k inte är större eller lika med (k + 1)2. |
Vi kan inte börja induktionsbeviset med 1. Gäller 2n ≥ n2 när n = 2? Ja, det gör det, men induktionssteget går fortfarande inte av samma anledning som förut. Induktionssteget gäller när n = 3 (byt ut 4 mot 3 ovan), men då stämmer inte induktionsbasen eftersom 23 < 32.
Vi ser att om vi börjar med ''fel'' tal, så är antingen induktionssteget eller induktionsbasen falsk (eller båda två).
Följande exempel handlar om Fibonaccitalen 1, 1, 2, 3, 5, 8, 13, 21, 34,…. Kanske har du sett dem förut? De upstår i naturen t.ex. som antalet spiraler i mitten av en solros. Om du vill veta mer om dem kan du t.ex. titta på http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html.
| Sats | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Låt f1 = 1, f2 = 1 och fn = fn–1 + fn–2 för n ≥ 3. Då gäller f1 + f2 + … + fn = fn+2 – 1, för alla heltal n ≥ 1. | ||||||||||||
| Kommentar | Bevis | |||||||||||
| Svåraste delen av detta bevis är att lista ut vad vi vill visa och vad som är definitionen. Meningen som börjar ''Låt'' är definitionen av fn så det är inte det som vi ska bevisa — vi tar det som ett fakta. Delen vi ska bevisa börjar med ''Då gäller…''. Vi måste också ha två basfall (n=1 och n=2) i induktionsbasen eftersom formeln i antagandet endast gäller för n större eller lika med 3. | I. Induktionsbas När n = 1 är vänsterledet lika med f1 = 1 och högerledet är f1+2 – 1 = f3 – 1 = f2 + f1 – 1 = 1 + 1 – 1 = 1. Alltså gäller f1 + f2 + … + fn = fn+2 – 1 för n = 1. När n = 2, är vänsterledet lika med f1 + f2 = 2 och högerledet är f2+2 – 1 = f4 – 1 = f3 + f2 – 1 = 2 + 1 – 1 = 2. Alltså gäller f1 + f2 + … + fn = fn+2 – 1 även när n = 2. |
|||||||||||
| Observera att vi inte bara använder induktionsantagandet, utan också definitionen fn = fn – 1 + fn – 2, där n = k + 2, som var given som ett antagande i satsen. | II. Induktionssteg Antag att f1 + f2 + … + fs = fs+2 – 1, för alla heltal s med 2 ≤ s ≤ k. Vi vill visa att f1 + f2 + … + fk+1 = fk+3 – 1. Betrakta vänsterledet: f1 + f2 + … + fk+1.
|
|||||||||||
| Som vanligt måste vi sluta med slutsatsen. | III. Slutsats Vi har visat att villkoren för induktionsprincipen gäller, så f1 + f2 + … + fn = fn+2 – 1 gäller för alla heltal n ≥ 1. |
|||||||||||
Bevisa följande påståenden med hjälp av induktion.
This note and any parts of it and any previous and future versions of it must not
be copied or disseminated in any printed or electronic form
or stored on any publicly accessible website without permission
from the author.
The author welcomes comments and corrections via email.
All contributions incorporated in updates of the manuscript will be acknowledged.
The author would like to thank the following for their contribution
to various updates of the original manuscript:
Sam Lodin, Fredrik Ståhl, Anders Gustafsson and Pia Heidtmann.