The algorithm described here can be performed on any weighted graph where there is some path between S and T. It finds the cheapest/quickest/lightest/shortest path from some S to T depending on what the weights on the graph represent. It can also be modified to find the most expensive/slowest/heaviest/longest path.
Example
Find a shortest path from S to T in the following graph.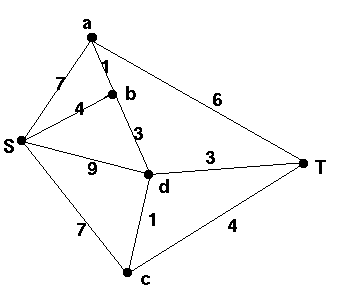
Method
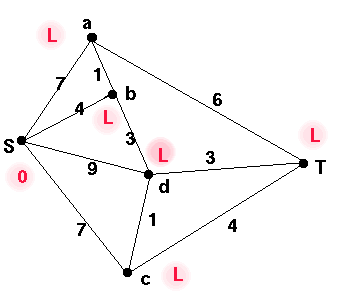 |
We start by assigning the temporary labels 0 to S and L to
the other vertices, where L represents a large number, larger
than the sum of all the weights in the graph. Temporary labels are written
in circles.
These are the maximum distances from S to each of the other vertices, which we will reduce as we analyse the graph.
| |||||||||||||||||||||
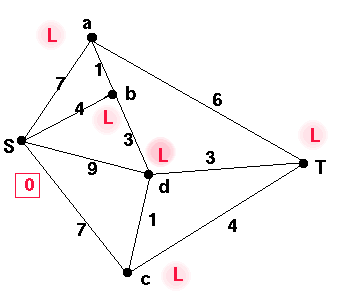 |
We choose the vertex k with smallest non-permanent label,
and make the label permanent. Permanent labels are written in a square.
In this case, it is S.
We write S in the second line in the table.
| ||||||||||||||||||||||||||||
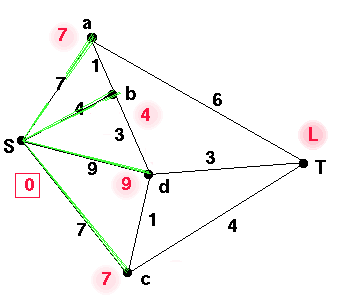 |
Now we check the neighbours x of S to see if the weight
of the edge Sx is less than the
current label for x.
If it is, then replace the old label, and entry in
the table, with this.
| ||||||||||||||||||||||||||||
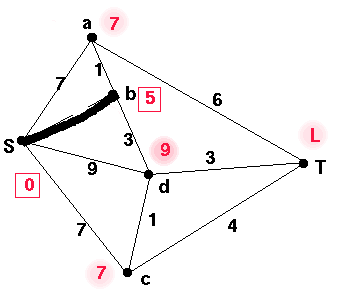 |
We choose the vertex k with smallest non-permanent label,
and make the label permanent. To find the edge which was
used to obtain that label, check back to the first row y in
which that label occured in k's column in the table. Then the
edge used was yk. In this case, it is b. We write b in the next line in the table. The first time we obtained the value 4, which is now b's permanent label, was in row S so the edge Sb was added to give us the value 4.
| |||||||||||||||||||||||||||||||||||
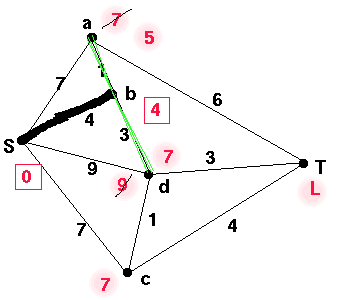 |
Let k be the current vertex under consideration in our table.
We check the neighbours x of k which have not already received
a permanent label, to see if the length
of the path to k (permanent label at k)
plus the weight of the edge kx is less than the
current label for x. If it is, then we replace the old label with
this sum. In this case, we look at the neighbours of b which are a and d. First we consider a. The temporary label at a is 7, and the edge from b to a is of weight 1, so weight of path to b + weight of edge ab = 5 which is less than 7 so we replace the 7 by 5. Similarly we replace the 9 by 7 at d. As b is not adjacent to c, we cannot change the label at c, and similarly we cannot change the label at T.
| |||||||||||||||||||||||||||||||||||
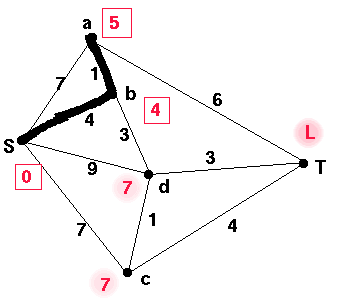  |
We repeat the process of assigning permanent labels and then checking for
shorter routes until T has received a permanent label. (The process
can be continued until all vertices receive a permanent label.)
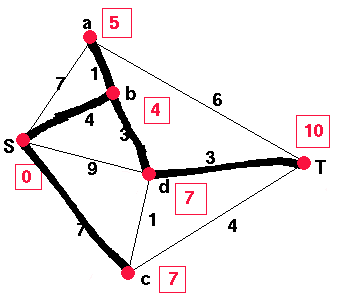
The smallest label is now 5 for a which was obtained using the edge ab. We now check the neighbours of a. As the weight of the path to a plus the weight of the edge aT is less than L, we replace L. a is not adjacent to any of the other vertices which have not received a permanent label so we can not change their labels. Continuing this process, we obtain the table below.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Conclusion
The permanent labels indicate the shortest route from S to each of the vertices. If all the vertices had a permanent label then the edges added to give the permanent labels form a spanning tree. Note that in general this is not a minimum spanning tree. In this example for instance, a minimum spanning tree for the graph above (found by Kruskal's algorithm) would have the edgesHowever, in general Dijkstra's algorithm does not give a minimum spanning tree. In the graph above, for example, consider the shortest path from S to c, it is found by Dijkstra's algorithm to be Sc of length 7. In the minimum spanning tree on the other hand, the path from S to c is Sbdc of length 8.
Exercises
(a) Find a shortest path in each of the graphs given below. Also give the lengths of the shortest paths and explain your method.(b) Further, find a minimum spanning tree in each of the graphs and check that you do not in general obtain the same spanning tree.
| 1 | 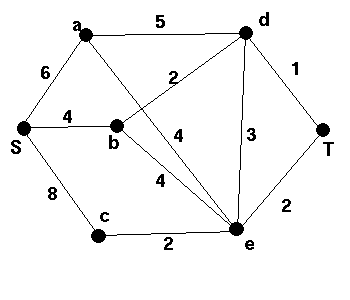 |
2 | 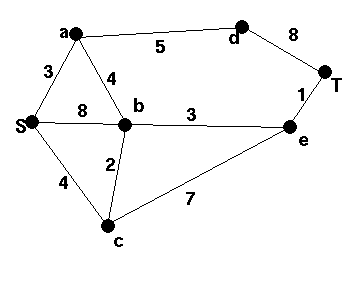 |
| 3 | 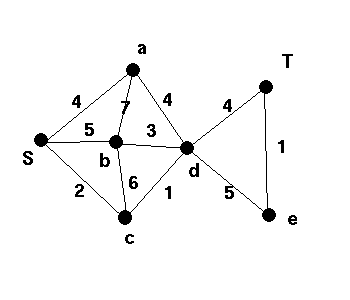 |
4 | 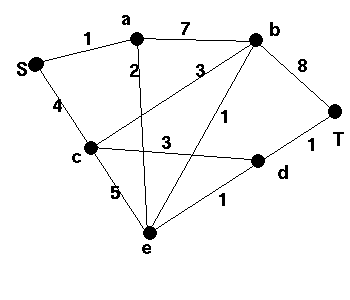 |
The author would like to thank the following for their contribution
to various updates of the original manuscript:
Pia Heidtmann.
© Sarah Norell
c/o Pia Heidtmann
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
c/o Pia Heidtmann
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
Updated 070811

