Grundläggande mängdlära och kombinatorik

Referenser

[J] Edition 5: Nedanstående text + [J] 2.1, 4.1, 4.2, 4.3
[J] Edition 4: Nedanstående text + [J] (2.1), (4.1), (4.2), (4.3)
[J] Edition 6: Nedanstående text + [J] [2.1], [6.1], [6.2], [6.3]

Bemärk, referenser i texten utan parenteser är till [J]ohnsonbaugh Edition 5, referenser i ()-parenteser är till [J] Edition 4, och referenser i []-parenteser är till [J] Edition 6.

Inledning

Målet med detta block är att lära oss de grundläggande begrepp och symboler, som används i förbindelse med mängder. Vi går igenom Venn-diagram och använder dessa till att illustrera diverse grundläggande mängdoperationer.

Vi skall också lära oss lite grundläggande kombinatorik. Kombinatorik är den gren av matematiken, som bl.a. handlar om hur man räknar ut antalet sätt att välja ut ett visst antal objekt med vissa villkor ur en given samling objekt, eller antalet sätt att utföra en serie handlingar med givna förutsättningar.

1. Mängder

Starta med att läsa avsnitt 2.1 i [J] från sidan 56 (64) [76] till och med exempel 2.1.3 (2.1.3) [2.1.5] på sidan 57 (65) [79].

Det är viktigt att förstå, att mängder ej är ordnade, dvs. man kan lista deras element i vilken ordning som helst, till exempel är

{1, 2, 5} = {1, 5, 2} = {5, 2, 1}.
Mängder har heller inga repeterade element, så till exempel

{1, 2, 5} = {1, 1, 5, 5, 5, 2}.
Glöm ej parenteserna '{' och '}', när du vill ange en mängd, till exempel är

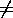{1, 2, 5} 1, 2, 5,
för vänstrasidan av detta uttryck är mängden bestående av elementen 1, 2 och 5, medan högrasidan är notationen för en ordnad följd bestående av elementen 1, 2 och 5 i den angivna ordningen. Lika viktigt är det att förstå, att man ej kan sätta ett godtyckligt antal parenteser, till exempel är

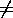{1, 2, 5} {{1, 2, 5}},
för vänstrasidan av detta uttryck är mängden bestående av elementen 1, 2 och 5, medan den högrasidan är en mängd bestående av blott ett element, nämligen mängden {1, 2, 5}.

Många små mängder anges lättast genom att lista alla mängdens element, på det sätt som vi har gjort i exemplen ovan. Ofta är det dock ej möjligt att lista alla element i en mängd, antingen av hänsyn till utrymme eller för att mängden är oändligt stor. I sådana fall är det ibland möjligt att ange de första få av mängdens element och eventuellt det sista elementet, om ett sådant existerar, och så använda symbolen '...' till att indikera, att alla mellanliggande värden också är inkluderade. Till exempel kan vi använda denna notation till att ange mängden av alla udda tal mellan 1 och 20:

{ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19} = {1, 3, 5, ... , 19}.
Högrasidan utläses som 'mängden bestående av (elementen) 1, 3, 5 och så vidare, upp till och med 19'. Vi brukar
'...'- notationen, när det är klart från kontexten vilka element som menas. Observera att '...'- symbolen består av precis tre prickar.

Några standardmängder, som vi ofta hänvisar till, har vi av bekvämlighetsskäl reserverade symboler för. Till exempel har du i gymnasiet kanske använt

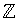	=	{ ... , -2, -1, 0, 1, 2, ... }, mängden av alla heltal;
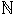	=	{0, 1, 2, 3, ... }, mängden av alla naturliga tal, och
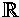,		mängden av alla reella tal.

Vi använder symbolen 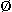till att beteckna den tomma mängden, dvs.

= { }.
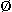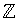
Lägg märke till att här sätter man inte parenteser om symbolerna. Till exempel är 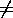{ 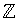},   för här är vänstrasidan mängden av alla heltal, medan högrasidan är en mängd bestående av blott ett element, nämligen .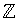

På sidan 56 (64) [77] beskrivs en viktig metod för att ange mängder med hjälp av  inklusionsregler. Inklusionsreglerna beskriver karaktäristiska egenskaper hos  mängdens element, så man kan skilja mellan dessa och element som ej är  inkluderat i  mängden. Till exempel har vi

{ x | x 10 och x är ett heltal } = {10, 11, 12, 13, ... },
där vänstrasidan utläses som 'mängden bestående av de (element) x som uppfyller att x är större än eller lika med 10 och x är ett heltal'. Vi påpekar att några författare brukar symbolen ':' i stället för '|' i denna notation, så vi har att

{ x | x 10 och x är ett heltal } = { x : x 10 och x är ett heltal } = {10, 11, 12, 13, ... }.

En mängds kardinalitet är antalet element i mängden. Detta begrepp  införs mitt på sidan 56 (64) [77]. Till exempel är

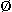| | = 0
och |{1, 2, 3, 7}| = 4.

På sidan 56 (64) [77] införs också symbolen '''', som utläses 'tillhör'.

Exempel
Om till exempel A = {0, 1, 2, 4}, så har vi

2 A,
som utläses ''(elementet) 2 tilhör (mängden) A'';
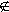3 A,
som utläses ''(elementet) 3 tilhör ej (mängden) A''.

Det är viktigt, att du känner till skillnaden mellan symbolerna '''' och 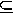 '' '' och ''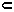'',  som införs i exempel 2.1.1 och 2.1.2 . Till exempel har vi

2 {0, 1, 2, 4},
{ 2 } {0, 1, 2, 4},
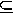{ 2 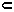} {0, 1, 2, 4}.
Vi har även att
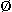
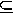{0, 1, 2, 4},
{0, 1, 2, 4},
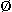
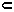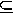{0, 1, 2, 4} {0, 1, 2, 4},
men märk väl, att där är en viktig skillnad på delmängder och äkta delmängder (engelska: proper subset): en mängd är ej en äkta delmäng av sig själv, så därför har vi
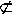{0, 1, 2, 4} {0, 1, 2, 4}.

På sidan 56 (65) [79] infördes notationen 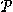(X)  till att beteckna potensmängden av en  mängd X. Vi märker här, att eftersom 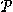(X)  är mängden bestående av alla  delmängder av X och den tomma mängden 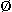är en delmängd av varje  mängd X (Varför?),  så är 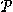(X) aldrig tom.

2. Multiplikationsprincipen

Läs nu avsnitt 4.1 (4.1) [6.1] i [J] från sidan 165 (197) [220] till och med exempel 4.1.3 (4.1.2) [6.1.3] sidan 168 (199) [223]. Här introduceras  multiplikationsprincipen, som är en mycket viktig grundläggande beräkningsprincip i kombinatorik och  sannolikhetslära.

Ändliga strängar, som uteslutande består av symbolerna 0 och 1, kallas binära strängar. Varje 0 och 1 i strängen kallas för en bit och en binär sträng med n bitar kallas en n-bit binär sträng eller en binär sträng av längden n. Till exempel är 001 en binär sträng med längden 3 och 00110011 är en 8-bit binär sträng.

Läs nu exempel 4.1.4 (4.1.3) [6.1.4] och 4.1.5 (4.1.4) [6.1.5] sidan 168 (200) [223]. Observera att  exempel 4.1.5 (4.1.4) [6.1.5] bevisar  följande sats:

Sats B1.1. Låt X vara en mängd med n element, då finns precis 2ⁿ element i potensmängden av X, dvs. |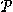(X)|= 2ⁿ.

Detta är sats 2.1.4 (2.1.4) [2.1.6] på sidan 57 (65) [79] i [J]. Innan vi fortsätter läsningen av [J] observerar vi, att vi också har följande sats:

Sats B1.2. Det finns 2ⁿ binära strängar av längden n.

Bevis. Vi kan konstruera en villkorlig binär sträng av längden n i n steg, där steg i, för i=1,2,... n, består av att välja den i:te biten i strängen. Eftersom vi har precis två möjligheter i varje steg, nämligen 0 eller 1, följer det av multiplikationsprincipen, att vi har 2ⁿ binära strängar av längden n.

3. Mera om mängder

Läs nu resten av avsnitt 2.1 i [J], men skippa beviset för sats 2.1.4 (2.1.4) [2.1.6] från överst på sidan 57 till mitten sidan 57 (nederst sidan 65  till mitten på sidan 66) [nederst sid 79 till övre bit sid 80], som vi bevisat ovan på annat sätt.

På sidan 57 (66) [80] införs först de viktiga mängdoperationerna (mängdunion), (mängdsnitt), och därnäst differensen av två mängder. Dessa kan illustreras med hjälp av såkallade Venn-diagram, som vi beskriver nedan.

Därnäst defineras två mängder X och Y till att vara disjunkta, om deras snittmängd är tom, dvs. om X Y = 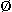. Till exempel är mängderna {1, 3, 5, 7, 9} och {2, 4, 6, 8, 10} disjunkta, för deras snittmängd är tom. Därimot är mängderna {1, 3, 5, 7, 9} och {1, 2, 3, 4, 5} inte disjunkta, för deras snittmängd är inte den tomma mängden, utan {1, 3, 5}.

En samling {X₁,X₂, X₃, ... , X _n} av mängder X_i, i=1,...,n, kallas parvis disjunkta, om för alla i, j = 1,2, ... , n där i 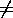j,
X_i X _j = .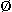

En partition av en mängd X är en samling av icke-tomma, parvis disjunkta delmängder av X, vars union är hela X.

Exempel
Låt till exempel U = {x 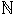| x är udda} och J = {x 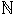| x är jämnt }, då har vi, att S={U, J} är en partition av ,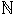
för varje tal i 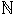är antingen jämnt eller udda, så U J = 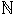och inget heltal är både jämnt och udda, så U J = .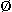

Överst på sidan 58 (67) [nederst sid 80] introduceras begreppet grundmängd (engelska: universal set). Det är viktigt att förstå, att det ofta är nödvändigt att specifiera grundmängden för att undgå tvetydiga definitioner. Betrakta till exempel mängden

{x | x<2}.
Om inte grundmängden är specificerat, är det omöjligt att se, om där menas

{x | x<2} = {0, 1},
vilket det skulle vara om grundmängden var 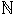, eller

{x | x<2} = { ... ,-2, -1, 0, 1},
vilket det skulle vara om grundmängden var 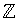, eller något helt annat. När vi anger mängder med hjälp av inklusionsregeln, specificerar vi därför alltid en grundmängd, utom när den är helt klar utifrån kontexten. I avsnitt 1 ovan betraktade vi till exempel mängden
{x | x 10 och x är ett heltal}.
Här har vi undgått tvetydigheter genom att ange inklusionsregeln ''x är ett heltal''. Tvetydigheter kunde också ha undvikits om vi hade specificerat grundmängden. Grundmängder angives oftast före ''|''- tecknet, så ovanstående mängd kan specificeras med:
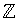{ x | x 10 },
vilket utläses 'mängden av x i (grundmängden) av alla heltal, som uppfyller att x är större än eller lika med 10'.

Venn-diagram

Ett Venn-diagram är en metod att illustrera, hur mängder från samma grundmängd är relaterade till varandra. Metoden är uppkallad efter dess uppfinnare, en engelsk matematiker med namnet John Venn, som levde på 1800-talet. I ett Venn-diagram illustreras grundmängden G med en stor rektangel och de i problemet givna mängder illustreras som överlappande områden (som regel cirklar) inuti rektangeln G. Om vi i en uppgift har två mängder S och T, bägge i samma grundmängd G, men i övrigt inte vet någonting om hur dessa är relaterade till varandra, ser Venn-diagrammet således ut:

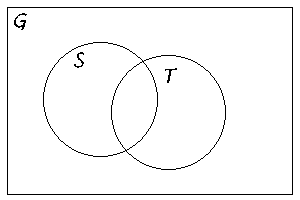
De fyra områdena i Venn-diagrammet svarar till, att det är precis fyra möjligheter för ett givet element x G, nämligen

1. x är i både S och T;
2. x är i S, men icke i T;
3. x är icke i S, men x är i T;
4. x är varken i S eller T.

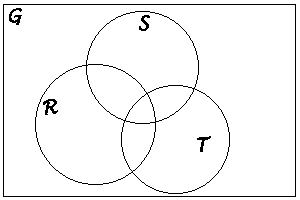
Om vi i en uppgift har tre mängder R, S och T , alla i samma grundmängden G, men i övrigt inte vet någonting om, hur dessa är relaterade till varandra, är det 8 möjligheter (varför?) för ett givet element x G, och det generella Venn-diagrammet för tre mängder partitionerar därför rektangeln G i 8 områden:

Mängdoperationer

Mängdunion

Unionen av två mängder S och T, S T, är mängden av alla de element, som tilhör en eller båda mängderna S och T.

Exempel
Om S = {1, 2, 3} och T = {2, 3, 4}, så är S T = {1, 2, 3, 4}.
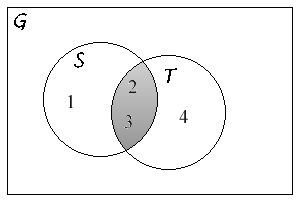
Detta kan illustreras således i ett Venn-diagram:

Mängdsnitt

Snittet av två mängder S och T, S T, är mängden, som består av alla de element, som är i både S och T.

Exempel
Om S = {1, 2, 3} och T = {2, 3, 4}, så är S T = {2, 3}.
Detta kan illustreras således i ett Venn-diagram:

Mängddifferens

Differensen av två mängder S och T, S - T, består av alla de element, som tillhör S , men icke tillhör T.

Exempel
Om S = {1, 2, 3} och T = {2, 3, 4}, så är S - T = {1}.
Detta kan illustreras således i ett Venn-diagram:

Observera, att generellt är S - T T - S.

Komplementmängd

Komplementmängden av en mängd S består av alla element i grundmängden G, som inte tilhör S.   kan därför beskrivas som G - S.

Exempel
Om G = 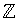och S = { x | x > 3 eller x < -1 }, så är 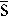= { -1,0,1,2,3 }.
Detta kan illustreras således i ett Venn-diagram:

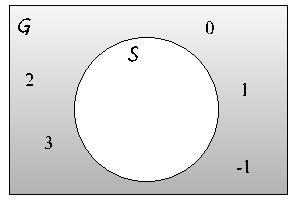
Observera att komplementmängden till en given mängd är beroende på grundmängden, medan unionsmängd, snittmängd och differensmängd är oberoende av grundmängden.

Mängdoperationerna, som vi illustrerade med Venn-diagrammen ovanför, är definerade på sida 57 (66) [80] i [J]. De uppfyller diverse räkneregler, varav de flesta är samlade i sats 2.1.10 (2.1.8) [2.1.12] i [J]. Du skall lära dig alla dessa räkneregler for mängdoperationer, men du behöver dock inte kunna bevisa dem.

På sida 61 (69) [83] införas den kartesiska produkten av två mängder. Nederst  på sidan 61 (69) [överst sid 84] noteras det, att för två mängder X och Y gäller det att

|X x Y| = |X| |Y|.
Detta följer av multiplikationsprincipen, då ordnade par kan beskrivas med en 2-stegs process, där första steget består att välja ett av de |X| elementen i X och andra steget består av att välja ett av de |Y| elementen i Y. På samma sätt följer också anmärkningen efter exempel 2.1.13 (2.1.13) [2.1.15] av multiplikationsprincipen. 

4. Additionsprincipen och sållningsprincipen

Läs nu resten av avsnitt 4.1 (4.1) [6.1] i [J] från sida 169 (201) [224] överst till sida 170 (203) [nedre del sid 225],  där kombinatorikens andra viktiga beräkningsprincip, additionsprincipen, gås igenom. Läs problem-lösnings hörnet
sida 172 - 174 (207 - 209) [228 - 229] i [J] extra grundligt, där det förklaras hur man arbetar sig fram till lösningen på ett kombinatorisk problem.

Märk väl att två godtyckliga mängder X och Y från samma grundmängd G inte  nödvändigtvis är disjunkta. Därför udvidgas additionsprincipen i [J] uppgift 65 (64) [65] sidan 172 (206) [227]. Låt oss lösa uppgiften tillsammans. Vi vill visa att

|X Y| = |X| + |Y| - |X Y|

Bevis:
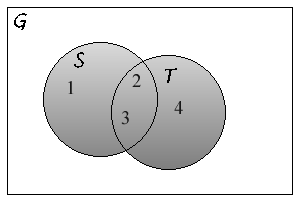
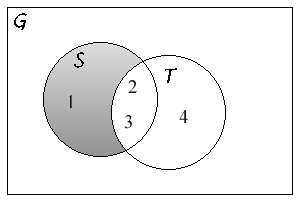
Denna formel ses lättast, om man ritar ett Venn-diagram för X och Y och numrerar de fyra disjunkta områden som följer:

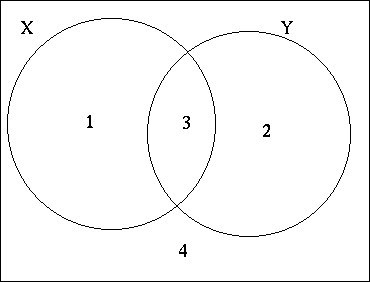
De fyra mängder, som ingår i formeln är då
 

X Y:		områdena 1, 2 och 3;
X:		områdena 1 och 3;
Y:		områdena 2 och 3;
X Y:		området 3.

Så vänstersidan av formeln är antalet av element i områdena 1,2 och 3, medans högersidan är antalet  element i områdena 1 och 3 plus antalet element i områdena 2 och 3 minus antalet element i område 3, dvs. högersidan är också antalet element i områdena 1, 2 och 3.

Man kan utvidga resultatet från uppg. 65 (64) [65] till tre (eller flera) mängder. Man kallar denna räknemetod sållningsprincipen eller inklusion-exklusions-principen (engelska: The Principle of Inclusion - Exclusion), och den betecknas PIE.

Sats B1.3
Låt X, Y och Z  vara tre mängder från samma grundmängd G, som inte nödvändigtvis är parvis disjunkta.
Då gäller att

|X Y Z| = |X| + |Y| + |Z| - |X Y| - |X Z| - |Y Z| + |X Y Z|.

Bevis:
Denna formel ses också lättast, om man ritar ett Venn diagram för X, Y och Z och numrerar de åtta disjunkta områden som följer:

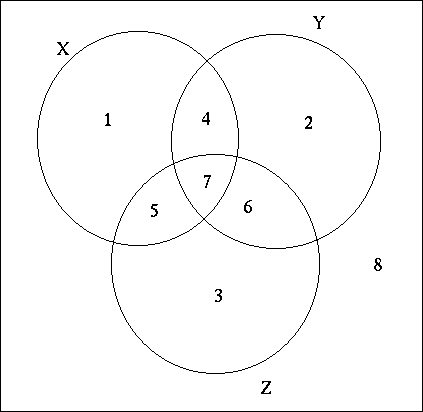
De åtta mängder, som ingår i formeln är då

X Y Z:		områdena 1, 2, 3, 4, 5, 6 och 7;
X:		områdena 1, 4, 5 och 7;
Y:		områdena 2, 4, 6 och 7;
Z:		områdena 3, 5, 6 och 7;
X Y:		områdena 4 och 7;
X Z:		områdena 5 och 7;
Z Y:		områdena 6 och 7;
X Y Z:		området 7.

På samma sätt som i exemplet med två mängder ovan ses då, att både vänstersidan och högersidan av formeln är antalet element i områden 1, 2, 3, 4, 5, 6 och 7.
 
 

5. Permutationer och kombinationer

Läs nu [J] 4.2 (4.2) [6.2]. I detta avsnitt introduceras först begreppet permutation. Generellt kallas en permutation av r objekt från en mängd med n element en r-permutation från n objekt, och är helt enkelt en ordnad lista av r objekt utvalda bland de n objekt i mängden utan upprepad användning av samma element.

Exempel
Låt t.ex. M = {a, b, c, d, e, f}, då är (a,b,c), (b,a,c), (f,a,b) och (b,a,f) exempel på 3-permutationer från M (Finns det fler?). Observera att vi använder rundade parenteser '(' och ')' omkring permutationer, eftersom permutationer är ordnade listor av element och inte bara mängder, dvs. permutationerna (a,b,c) och (b,a,c) är  olika, fastän de består av  samma element.

Antalet  r-permutationer från en mängd med n element kallas

P(n, r),
och det visas med hjälp av multiplikationsprincipen (jmf. [J] sida 177 (213) [232]), att

P(n, r)

=

n!  (n - r)!

Exempel
Låt t.ex. M = {a, b, c, d, e, f}. Antalet  3-permutationer från M är P(6, 3) = 6x5x4 =120.
 

När vi beräknar permutationer, är ordningen av  elementen viktig, dvs. när vi har samma element, men i en annan ordning, så är de två permutationerna olika. Det nästa, som definieras i [J] är kombinationer. Här är ordningen av elementen utan betydelse. En r-kombination från en mängd M med n element är endast en delmängd av M, som innehåller r av M:s element.

Exempel
Låt M = {a, b, c, d, e, f}, då är t. ex. {a, b, c} och {f, a, b} exempel på 3-kombinationer från M. Observera att vi använder krullparenteser '{' och '}' omkring kombinationer, eftersom kombinationer är mängder, dvs. oordnade listor av element. Kombinationerna {a,b,c} och {b,a,c} är alltså desamma, eftersom de innehåller precis samma element, och ordningen av elementen saknar betydelse.
 

Antalet  r-kombinationer från en mängd med n element kallas  i [J]  för C(n, r), och det visas på sidan 179 (216) [233], att

C(n, r)

=

P(n, r) r!

Dvs. vi har att

C(n, r)

=

n! r! (n - r)!

Exempel
Låt t.ex. M = {a, b, c, d, e, f}. Antalet  3-kombinationer från M är C(6, 3) = (6x5x4)/(3x2x1) =20.

Notationen C(n, r), som [J] använder för att beteckna antalet r-kombinationer, är inte helt standard. De flesta författare använder notationen

(

n r

)

=

C(n, r).

Exempel
Låt t.ex. M = {a, b, c, d, e, f}. Antalet 3-kombinationer från M är

(

6 3

)

=

C(6, 3)  = 20.

Du skall känna till och kunna använda båda notationerna för kombinationer.

Läs nu [J] 4.3 (4.3) [6.3]. I detta avsnitt visas algoritmer för att skriva  ut permutationer och kombinationer. Dessa är viktiga för dig, om du kommer att använda en dator för att arbeta med kombinationer och permutationer.

 

6. Förslag till övningsuppgifter

Övningsuppgifter från [J]

[J] sida 62-63:
Uppg. 1-15, 31-38, 40, 41, 43-52 , 54-64, 69, 71-74, 79
(sida 71-72: 1-38, 40-50, 55, 57-60, 65)
[sida 85-86 1-15, 32-39, 41, 42, 44-53, 55-65, 70, 71-74, 79]

[J] sida 171-174:
Uppg. 1, 4, 8, 10, 12, 17, 20-23, 26, 28, 29, 34-41, 42-45, 48, 54, 57, 66-70
(sida 203-205: 1, 4, 7, 9, 11, 16, 19-22, 25, 27, 28, 33-39, 41-44, 47, 53, 56, 65-69)
[sida 226-227: 1, 4, 8,10, 12, 17, 20-23, 26, 28, 29, 34-41, 42-45, 48, 54, 57, 66-70]

[J] sida 182-184:
Uppg. 1-7, 10-13, 15, 19-21, 25-29, 31-33, 38, 58-62.
(sida 220 - 224: 1-7, 10-13, 15, 19-21, 25-29, 31-33, 38, 58-62)
[sida 237-239: 1-7, 10-13, 15, 19-21, 25-29, 31-33,  38, 58-62]

Extra övningsuppgifter till Venn-diagram

1. Låt A, B och C vara tre godtyckliga mängder. Rita upp ett Venn-diagram och markera mängden (A-B) (C-B).
   
2. Låt A, B och C vara tre godtyckliga mängder. Rita upp ett Venn-diagram och markera mängden (A C) - B
3. Är de resulterande mängderna i 1 och 2 lika?