Mera om heltal

Referenser

[J] Edition 5: Nedanstående text + [J] 3.3 (från Sats 3.3.4 sidan 129) och [J] 3.4.

[J] Edition 4: Nedanstående text + [J] (3.3) (från Sats 3.3.4 sidan 152 och [J] (3.4).

[J] Edition 6: Nedanstående text + [J] Sats 5.1.3 sid 184, [J] [5.3] (sid 205 t.o.m. Example 5.3.4 sid 207) och [J] [4.4]

Bemärk, referenser i texten utan parenteser är till [J]ohnsonbaugh Edition 5, referenser i ()-parenteser är till [J] Edition 4, och referenser i []-parenteser är till [J] Edition 6.

Observera att sättet materialet i [J] 3.3 i 4 utgåvan framställs på skiljer sig avsevärt  från sättet materialet framställs i 5 utgåvan, ävenså 6 utgåvan.)

Inledning

I detta block skall vi se närmare på några fundamentala egenskaper hos heltal. Vi skall först gå igenom delare och primtal, och därnäst skall vi se, att det finns ett mycket viktigt samband mellan den största gemensamma delaren av två heltal och linjärkombinationerna av dessa två heltal. Vi skall också gå igenom Euklides algoritm, som är en metod för att hitta den största gemensamma delaren av två heltal. Det mesta av innehållet i detta block är inte behandlat så detaljerat i [J], så nedanstående text är därför huvudreferensen.

1. Delare och primtalsfaktorisering

Ett heltal b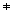 0 sägs  vara en delare (också kallad en faktor) till heltalet a, om det finns ett heltal k, som vi kallar kvoten, sådan att a=bk. Med matematiska symboler skriver vi detta på formen b | a och vi läser det som 'b delar a'.  Om ett heltal b inte är en delare till a, indikerar vi detta genom att sätta ett streck över '|'-symbolen, dvs. vi skriver b a och läser detta som 'b delar inte  a'. 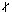Observera att det lodräta strecket i denna notation inte är ett bråkstreck, 'b | a' skall inte förväxlas med 'b/a'.

Om  b | a säger vi att a är en multipel av b, och uttrycket a=bk kallas en faktorisering av a.

Talen 1 och -1 är speciella heltal, när vi talar om faktorisering, eftersom de delar alla heltal. Vi har därför ett speciellt namn för dessa två tal, de är så kallade enheter i 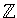. Varje heltal a har naturligtvis de två triviala faktoriseringarna

a=(a)(1) och a=(-a)(-1),

dvs. 1, -1, a,  och -a är alltid delare till heltalet a om a 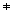0. Vi kallar ett heltal b 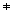0 för en äkta delare till a, om b | a och b inte är en av delarna 1, -1, a,  eller -a. Ett heltal a, som har en äkta delare kallas för ett sammansatt tal.

Exempel

• 6 är ett sammansatt tal, eftersom 6=(2)(3) och 6 har därför 2 och 3 som äkta delare.

• Ett godtyckligt heltal b 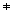0 är en delare till 0, eftersom 0=(b)(0), så 0 har (oändligt) många äkta delare och är därför ett sammansatt tal.

• -1 och 1 är inte sammansatta tal, eftersom de enda delarna till -1 och 1 nämligen är 1 och -1 själva.

Vi börjar med några  fundamentala resultat för delare:

Sats B3.1.
Låt m, n och c vara heltal sådana att c | m och c | n.
Då gäller att c | (m+n) och c | (m-n).

Bevis.
Eftersom m och n bägge har c som delare kan vi hitta två kvoter q₁ och q₂, bägge heltal, sådana att
m=cq₁ och n=cq₂. Därför är

m+n=cq₁+cq₂= c(q₁+q₂), så c är alltså en faktor i m+n, dvs. c | (m+n).

På samma sätt har vi att m-n=cq ₁-cq₂ =c(q₁-q₂), så c är också en faktor i m-n, dvs. c | (m-n).
 

Sats B3.2.
Låt m, n och c vara heltal, som uppfyller att c | m och m | n.
Då har vi att c | n.

Bevis.
Eftersom m  har c som delare kan vi hitta en heltalskvot q₁ sådan att
m=cq₁. På samma sätt har vi att n har m som delare, så det existerar också ett heltal q₂ sådant att n=mq₂.
Vi har därför att n=mq₂ =(cq₁)(q₂ )=c(q₁q₂), och c är därför också en faktor i n, dvs. c | n. 

Definition
Ett primtal, p, är ett heltal, som
(i)  inte är en enhet och
(ii) inte har äkta delare.

Observera  att denna definition medför, att det existerar både negativa och positiva primtal:

Exempel

• 2 är ett primtal, eftersom 2 inte är en enhet och de enda delarna till 2 är 1, -1, 2 och  -2, så 2 har inga äkta delare.


• -2 är ett primtal, eftersom -2 inte är en enhet och de enda delarna till -2 är 1, -1, 2 och -2, så -2 har inga äkta delare.


• -1 och 1 är inte primtal, eftersom de är enheter.

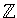Vi observerade ovan, att enheterna -1 och 1 varken är primtal eller sammensatta tal. Vi  har därför med ovanstående definitioner partitionerat (jmf. avsnitt 3 i läsanvisningen till block 1) heltalen i tre disjunkta delmängder:

Enheter = {-1, 1},

Primtal = { 2, -2, 3, -3, 5, -5, 7, -7,  . . .} och

Sammansatta tal = {0, 4, -4, 6, -6, 8, -8, 9, -9, 10, -10,  . . .}

Matematiker har ända sedan antiken forskat om primtal, men trots detta finns det än i dag många olösta problem omkring primtal. Ett av de största problemen var länge att hitta en snabb algoritm för att bestämma om ett givet heltal n är ett primtal eller ej. Detta problem blev dock löst 2002 av två studenter vid Indian Institute of Technology i Kanpur vid namn Kayal och Saxena, när de hittade den så kallade AKS-algoritmen tillsammans med deras handledare Agrawal. Vi skall inte lära oss AKS-algoritmen på denna kurs, men det är bra att veta att den existerar, om du skulle få användning för den i framtiden. Låt oss i stället se på några primtalstest som fungerar för små tal, där problemet inte är så stort och svårt, att det är nödvändigt med smarta algoritmer. Man kan t.ex. prova sig fram med alla möjliga delare:

Exempel
Låt oss undersöka, om 151 är ett primtal.

Vi kan självklart lösa detta problem genom att dela 151 med alla talen 2, 3, 4, 5, 6, ..., 150 och därmed kontrollera om ett av dessa delar 151; men detta kräver 149 divisioner och tar lång tid! Om vi tänker oss för, kan vi kanske hitta på en mer effektiv metod...

Vi observerar först, att 2 inte delar 151. Är det då möjligt att 4 delar 151? Eller 6? Eller 8, 10, 12, 14,..., 150?
Svaret är nej, eftersom det ur sats B3.2 följer, att om heltalet 2k delar 151, då delar 2 också 151 eftersom 2 delar 2k. På liknande sätt ses, att eftersom 3 inte delar 151, så delar ingen multipel av 3 talet 151 heller.
Slutsatsen är, att vi, på grund av sats B3.2, endast behöver kontrollera, om alla primtal mindre än 151 är delare till 151. Detta reducerar problemet en hel del, men det är fortfarande för många tal att kontrollera, så vi tänker oss för lite till...

. . . och vi inser då, att om det finns två heltal a och b, sådana att 151=ab, måste minst ett av dessa vara mindre än eller lika med 13 (Varför? Ledning: om både a och b är större än 13, hur stort är talet ab då?).

Vi kan därför nöja oss med att kontrollera om 2, 3, 5, 7, 11 och 13 delar 151, och eftersom inget av dem gör det, kan vi dra slutsatsen att 151 är ett primtal. Det krävs alltså endast 6 divisioner för att slå fast att 151 är ett primtal.

Exempel
Hur många divisioner krävs för att kontrollera om 397 är ett primtal? Svar: 8
(nämligen division med 2, 3, 5, 7, 11, 13, 17 och 19)

Metoden från föregående exempel med att kontrollera alla möjliga primtalsdelare upp till 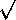n är tillräckligt bra för att kontrollera om små tal n är primtal; men om n är ett stort tal, t.ex. med 1000 siffror eller fler, så är denna metod inte tillräckligt effektiv, inte ens med hjälp av dagens snabbaste datorer. Det är ett öppet forskningsproblem, om det existerar en mycket snabb algoritm som kan faktorisera alla heltal, även mycket stora, dvs. skriva dem som en produkt av två äkta delare. Ett av nutidens mest använda krypteringssystem (ett krypteringssystem är ett system för utväxling av hemliga meddelanden), det så kallade RSA-krypteringssystem, bygger på, att faktorisering av stora tal är ett mycket svårt matematisk problem, så om du har lust, tid och goda ideer finns det här en möjlighet till att bli berömd!

2. Linjärkombinationer och största gemensamma delare.

Om m och n är heltal, kallar vi varje heltal på formen sm+tn, där s och t också är heltal, för en linjärkombination av m och n.

Exempel
Om t. ex. m=3 och n=7, så är alla följande tal linjärkombinationer av m och n:

 3 :    låt s=1 och t=0, då är 3= (1)(3)+(0)(7);
 7 :    låt s=0 och t=1, då är 7= (0)(3)+(1)(7);
 0 :    låt s=0 och t=0, då är 0= (0)(3)+(0)(7);
-7 :    låt s=0 och t=-1, då är -7= (0)(3)+(-1)(7);
40:    låt s=-3 och t=7, då är 40= (-3)(3)+(7)(7).

Uppgift B3.1
Prova nu att skriva vart och ett av talen i ovanstående exempel som en linjärkombination av 3 och 7, där värdena av s och t är andra än de som givits i exemplet.

Vi bevisar en sats, som utvidgar sats B3.1 till att gälla inte bara för m+n och m-n utan för alla linjärkombinationer av m och n:

Sats B3.3.
Låt m och n vara heltal och låt d vara ett heltal, som delar både m och n ( ett sådant tal kallas en gemensam delare till m och n), dvs. d | m och d | n. Då gäller för alla heltal s och t, att d | (sm+tn).

Bevis.
Eftersom m och n båda har d som delare kan vi hitta två kvoter q₁ och q₂, båda heltal, sådana att m=dq₁ och n=dq₂. Därför är

sm + tn = s(dq₁) + t(dq₂) = d(sq₁ + tq₂),
så d är alltså en faktor i sm+tn, dvs. d | (sm+tn). 

Uppgift B3.2
(a) Finn alla heltal mellan -12 och 12 som är linjärkombinationer av 3 och 7;

(b) Finn alla heltal mellan -12 och 12 som är linjärkombinationer av 4 och 6;

(c) Finn alla heltal mellan -12 och 12 som är linjärkombinationer av 6 och 9.

Du fann förhoppningsvis i uppgift B3.2(b) att 2 är delare i alla linjärkombinationer av 4 och 6, och i B3.2(c) att 3 är delare i alla linjärkombinationer av 6 och 9. Kan du se ett samband mellan 2 och talen 4 och 6? Är det kanske ett liknande samband mellan 3 och talen 6 och 9? Vi ska svara på denna fråga lite senare i detta avsnitt. Betrakta först följande definition:

Definition
Låt m och n vara två heltal, som inte båda är noll, och låt s vara ett positivt heltal som uppfyller följande två krav:

(i) s | m och s | n, och

(ii) om d | m och d | n så gäller att d |s,

då kallas s för den största gemensamma delaren (förkortas sgd) till m och n. Vi skriver detta som sgd(m,n). På engelska kallas största gemensamma delaren för greatest common divisor, och man använder därför förkortningen gcd och skriver alltså gcd(m,n).

Låt oss se lite närmare på definitionen av sgd:

För det första är sgd(m,n) alltid ett positivt heltal. Därutöver säger det första kravet, att sgd(m,n) är en gemensam delare till m och n, dvs. sgd(m,n) delar både m och n. Det andra kravet är lite mera invecklat. Det säger, att varje delare till både m och n också är en delare till sgd(m,n). Detta medför att sgd(m,n) är den numeriskt största gemensamma faktor i m och n (varför?). För små tal, är det mycket lätt att hitta den största gemensamma delaren:

Exempel
sgd(3,7)=1;
sgd(4,6)=2;
sgd(6,9)=3;
sgd(-4,6)=2 (varför är den inte -2?);
sgd(-4,-6)=2  (varför är den inte -2?);

Huvudresultatet, som du skall känna till för största gemensamma delare är följande viktiga sats, som vi skall använda senare, men som vi inte skall bevisa i denna kurs.

Sats B3.4
Låt m och n vara två heltal som inte båda är noll, då existerar deras största gemensamma delare sgd(m,n), och det existerar dessutom heltal s och t så att sgd(m,n) =sm+tn.  

Satsen säger, att  den största gemensamma delaren till m och n existerar och kan skrivas som en linjärkombination av m och n. Slås detta ihop med sats B3.3 fås följande följdsats:

Följdsats B3.5.

Låt m och n vara två heltal, som inte båda är noll och låt g= sgd(m,n). Låt vidare

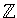L={x |  x=am+bn,  a,b  }       och       M={kg |  k }
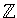dvs. L är mängden av linjärkombinationer av m och n, och M är mängden av multipler av sgd(m,n).
Då är L=M.

Denna följdsats är resultatet, som ligger till grund för observationen efter uppgift B3.2 (se uppgift B3.3 nedan). Vi vill nu bevisa denna följdsats. Du kommer inte att examineras på detta bevis, men det innehåller en detalj, som du kan bli ombedd  att förklara: Om man skall visa, att två mängder är lika, här att M=L, då visar man  (i) att M 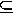L,  och (ii) att L 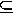M, och drar slutsatsen att M=L. Varför är detta sant? (Ledning: Rita Venn diagram!)

Bevis (följdsats B3.5).
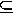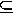För att visa, att de två mängderna M och L är lika, visar vi (i) att M L  och (ii) att L M:

(i) Sats B3.4 ger att g tillhör L. Så antag att s och t är sådana heltal att g= sm+tn. Då är multiplen

kg = k(sm + tn)=(ks)m + (kt)n
för varje heltal k. Därför är M 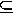L.

(ii) Låt nu j vara ett element i L, dvs. j=s₁m+t ₁n, där s₁ och t₁ är heltal. Eftersom g | m och g | n har vi ur sats B3.3 att g | (s₁m+t₁n), så det existerar alltså ett heltal k sådant att (s₁m+t₁n) =kg; men det betyder att j också är ett element i M, så därför är L 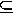M.   

Uppgift B3.3
Använd resultatet av Följdsats B3.5 för att hitta elementen i följande mängder
(a) L={x |  x=s3+t7,  s,t  };

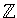(b) L={x |  x=s4+t6,  s,t  };

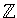(c) L={x |  x=s6+t9,  s,t  }.

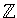Jämför dessa resultat med resultaten i uppgift B3.2.

3. Euklides algoritm

I  föregående avsnitt fann vi att om man vill hitta alla möjliga linjärkombinationer av två heltal (som inte båda är noll), så är det tillräckligt att känna till deras största gemensamma delare. I de exempel vi studerade, var det relativt lätt att hitta sgd(m,n), eftersom m och n var små tal; men om vi vill hitta sgd(m,n) där m och n är stora tal, t.ex.  sgd(15939,9367), vad göra?

Sats B3.4 garanterar att sgd(15939,9367) existerar, men den säger inte hur vi i praktiken hittar den största gemensamma delaren. Lyckligtsvis finns en gammal algoritm som är särskilt effektiv för att beräkna största gemensamma delaren till två heltal. Algoritmen går under namnet Euklides algoritm, då den finns beskriven i Euklides 'Elementa' (cirka 300 F. Kr.), och den är än idag den mest effektiva algoritm man känner till för detta syfte.

Euklides algoritm kan för övrigt också användas för att hitta en linjärkombination av två heltal som är lika med sgd(m,n).  Återigen garanterar sats B3.4, att en sådan linjärkombination existerar, men den säger inte, hur vi kan hitta den.

Vi ska i resten av detta avsnitt anta att m och n båda är positiva heltal. Vi förlorar inget på att anta detta, eftersom vi har följande sats:

Sats B3.6
Låt m och n vara heltal och antag att sgd(m,n) existerar. Då är sgd(m,n) =sgd(|m|,|n|).

Bevis.
Detta följer av, att om d | m, så har vi också att d | (-m) (Varför?). 

Euklides algoritm bygger på Divisionsalgoritmen, som vi beskrev i avsnitt 5 i läsanvisningen till block 2.
Euklides algoritm är följande:

Euklides Algoritm

• Antag, att m och n är två positiva heltal, och att vi vill beräkna sgd(m,n).
• Använd först Divisionsalgoritmen för att dela m med n,
  varvid vi får en rest r₁, där 0 r₁ <  n.
•  Om r₁ 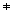0, då delar vi n med r₁ och får en rest r₂ , där 0   r₂ < r ₁.
•  Om r₂ 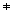0, då delar vi r₁ med r₂ och får en rest r₃ , där 0   r₃ < r ₂.
•  Om r₃ 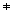0, då delar vi r₂ med r₃ och får en rest r₄ , där 0   r₄ < r ₃.
•  Om r₄ 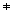0, då delar vi r₃ med r₄ och får en rest r₅ , där 0   r₅ < r ₄.

   .
   .
   .
 
• Så fortsätter vi, tills vi vid en tidpunkt får resten 0.
• Om denna rest är r_k, dvs. r_k=0 och r_i 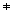0 for i < k,
  då är sgd(m,n)=r_k-1.
• sgd(m,n) är alltså den sista resten, som inte är noll.

Exempel
Låt oss använda Euklides algoritm för att hitta sgd(m,n) då m= 54  og n=33:

54 = 33(1) +  21   [dela m=54 med n=33, rest r₁ = 21]
33 = 21(1) +  12   [dela n= 33  med r₁=21, rest r₂=12]
21 = 12(1) +   9    [dela r₁=21 med r ₂=12, rest r₃= 9]
12 =   9(1) +   3    [dela r₂=12 med r₃=  9, rest r₄=3]
  9 =   3(3)           [dela r₃=  9 med r₄=  3, rest r₅ =0 ]

Enligt Euklides algoritm är sgd(54,33) = 3, dvs. den sista rest, som inte är noll.

Läs nu avsnitt 3.3 i [J]  från och med sats 3.3.4 sidan 129 (152) t.o.m. sidan 131 (156) [sats 5.1.3 sidan 184 och 5.3 sidan 205 t.o.m. Example 5.3.4 sida 207]. Här beskrivs Euklides algoritm igen,  och man förklarar hur den fungerar. Vi ger ytterligare ett exempel, denna gång försöker vi hitta största gemensamma delaren till två tal som inte omedelbart kan faktoriseras.

Exempel
Låt oss hitta sgd(15939, 9367) med hjälp av Euklides algoritm:

15939 = 9367(1) + 6572
  9367 = 6572(1) + 2795
  6572 = 2795(2) + 982
  2795 =   982(2) + 831
    982 =   831(1) + 151
    831 =   151(5) +   76
    151 =     76(1) +   75
      76 =     75(1) +     1
      75 =       1(75)

Så sgd(15939, 9367) =1.

När sgd(m, n) =1, så har talen m och n ingen gemensam delare förutom enheterna  1 och -1. Sådana heltal säges vara relativt prima. Observera att tal kan vara relativt prima, även om inget av dem är primtal, t.ex. är 12 och 35 relativt prima.  

Sats B3.7
Låt m och n vara heltal, som inte är noll.
Då är m och n relativt prima om och endast om det existerar två heltal a och b så att am + bn = 1.

Bevis
(==>) Antag, att m och n är relativt prima, dvs. sgd(m,n)=1. Sats B3.4 ger då, att det existerar heltal a och b sådana att sgd(m,n)=am+bn, dvs. 1 = am + bn.

(<==) Antag, att det existerar heltal a och b sådana att 1 = am + bn, och låt sgd(m,n)=s. Eftersom s | m och s | n, har vi ur Sats B3.3 att s | am + bn, dvs. s | 1, och därför är s =-1 eller s=1. Utav definitionen av sgd har vi dock, att s är positiv, så därför kan vi konkludera, att s=1.   

Som nämnts ovan, kan Euklides algoritm användas för att hitta en linjärkombination av två heltal m och n som är lika med sgd(m,n).  Detta görs genom att först skriva om alla ekvationerna i algoritmen till att ge ett uttryck för resterna och arbeta sig upp genom algoritmen bakifrån. Detta illustreras lättast genom ett exempel:

Exempel
Vi fann ovan, att sgd(54, 33)= 3 i följande fyra steg, som vi först skriver som

54 = 33(1) +  21      ==>    21  = 54 - 33(1)
33 = 21(1) + 12       ==>    12  = 33 - 21(1)
21 = 12(1) +   9       ==>      9  = 21 - 12(1)
12 =   9(1) +   3       ==>      3  = 12 -   9(1).

Vi börjar med den fjärde ekvationen, som uttrycker sgd(54, 33)= 3 som en linjärkombination av 12 och 9. Därnäst substituerar vi den tredje ekvationen in i uttrycket, förenklar det, substituerar sedan den andra ekvationen in i uttrycket, förenklar igen, etc. :

3 = 12 + 9(-1)

   = 12 + [21-12(1)] (-1)       [här substituerar vi in 3. ekvationen]

   = 12(2) +21(-1)                 [förenkling ] [Koll: HL =24 - 21 = 3]

   = [33-21(1)](2)  + 21(-1)   [här substituerar vi in 2. ekvationen ]

   = 33(2) +21(-3)                 [förenkling ] [Koll: HL =66 - 63 = 3]

   = 33(2) +[54 -33(1)] (-3)   [här substituerar vi in 1. ekvationen]

   = 33(5) +54(-3)                 [förenkling ] [Koll: HL =165 - 162 = 3]

Från den sista ekvationen fås nu, att 3 = 54a + 33b, där a = -3  och b = 5.

Processen som beskrivs i detta exempel är inte särskilt svår, men det är mycket lätt att göra ett räknefel. Vi föreslår därför att alltid sätta runda parenteser omkring kvoter eller att stryka under alla rester, så att man kan se skillnad på kvoterna och resterna. Ett annat tips är att efter varje förenkling, kontrollera att högerledet är lika med den största gemensamma delaren, såsom vi har gjort i exemplet ovan. Om du följer dessa två huvudregler, skall det vara möjligt att göra dessa beräkningar utan fel.

4. Primtalsfaktorisering

Vi presenterar nu en mycket viktig egenskap hos primtal. Låt oss först formulera resultatet:

Sats B3.8.
Låt m och n vara heltal som båda är skilda från noll, och låt p vara ett primtal så att  p | mn, då gäller antingen att p | m eller att p | n   (eller p delar båda).

Exempel
Låt m = 36, då finns det många olika faktoriseringar av 36 med två faktorer, t.ex.

36 = 36·1 = 18·2 = 12·3 = 9·4 = 6·6 = (-6)·(-6) = (-9)·(-4) = . . .

De enda primtal, som är delare till 36 är -2, 2, -3 och 3, och sats B3.8 säger, att varje gång vi har en faktorisering av 36  med två faktorer, så delar dessa minst en av faktorerna. Tag t.ex. p=3: i faktoriseringen 36·1 delar 3 den första faktorn, i faktoriseringen 18·2 delar 3 den första faktorn,  i faktoriseringen 12·3 delar 3 den första och också den andra faktorn, etc.

Låt oss nu bevisa sats B3.8:

Bevis (sats B3.8).
Låt m och n vara heltal, som båda är skilda från noll, och låt p vara ett primtal sådant att p | mn. Vi skall visa, att p delar minst en av faktorerna m och n, dvs. vi skall visa, att om p inte är en faktor i m, då är p en faktor i n.

Antag därför, att p inte är en faktor i m. Eftersom p är ett primtal har det endast de fyra faktorerna p, -p, 1 och -1, och eftersom m inte är noll betyder detta, att p och m är relativt prima. Av sats B3.7 har vi då, att det existerar heltal a och b sådana att

1= ap + bm.
Låt oss nu multiplicera denna ekvation med n, då får vi
     n= apn + bmn.
Vi vet också (av antagandet), att p | mn, så det existerar alltså en heltalskvot k sådan att mn = kp. Om vi sätter in detta i uttrycket för n fås
n= apn + bmn = apn + bkp = p(an+bk),
varav det ses, att p | n.

Vi avslutar detta avsnitt med en av algebrans huvudsatser. Den säger att alla heltal är uppbyggda av primtal. Vi ska inte bevisa denna sats på den här kursen, men nämner, att sats B3.8 är en av hörnstenarna i beviset:

Sats B3.9 (Aritmetikens fundamentalsats)
Varje heltal (utom noll) kan skrivas som en produkt av precis en enhet och ett ändligt antal positiva primtal.
Det gäller ytterligare, att denna faktorisering är entydig sånär som på faktorernas ordning.
 

Exempel
Vi skriver 6 som en produkt av en enhet och primtal:

6 = (1)(2)(3),
enheten är här 1, och det är två positiva primtalsfaktorer, nämligen 2 och 3. Att faktoriseringen  är entydig sånär som på faktorernas ordning betyder att de sex faktoriseringarna

6 = (1)(2)(3) = (1)(3)(2) = (2)(1)(3) = (2)(3)(1) = (3)(1)(2) = (3)(2)(1)
alla uppfyller satsens betingelser; men att vi inte räknar dem som fundamentalt olika.

5. Rekursiva algoritmer och definitioner

Läs nu avsnitt 3.4 (3.4) [4.4] i [J], det handlar om rekursiva algoritmer och definitioner. I detta avsnitt gås en rekursiv version av Euklides algoritm igenom, men även n! (läses 'n fakultet') defineras och Fibonacci-talen, som vi set på i block 2.
 

6. Förslag till övningsuppgifter

Övningsuppgifter från [J]

[J] sida 131:
Uppg. 1-9, 16, 18
(sida 156-157: 7-15, 20, 22 )
[sida 213: 1-9, 15, 11]

(Metoden om det hänvisas till i uppg. 18 (22) [11] är samma metod som att gå igenom Euklides algoritm bakifrån, som vi har beskrivit ovan).

[J] sida 137 :
Uppg. 1, 4, 5, 20, 21.
(sida 163-165: 1, 4, 5, 13, 14)
[sida 179: 1, 18, 19 ]

Extra övningsuppgifter i linjärkombinationer och aritmetikens fundamentalsats

(a) Skriv 1 som en linjärkombination av 15939 och 9367;

(b) Skriv 5 som en linjärkombination av 15939 och 9367;

(c) Skriv 100 som en linjärkombination av 15939 och 9367;

(d) Skriv 60 som en produkt av en enhet och positiva primtal;

(e) Skriv -60 som en produkt av en enhet och positiva primtal;

(f) Skriv -3 som en produkt av en enhet och positiva primtal.