Block 5 Algebra och Diskret Matematik A

Logik, bevis och rekursionsformler

Referenser

[L]ogik och [B]evis av Sarah Norell, nedanstående text samt
[J] Edition 5: 1.4, 1.6, Exempel 5.1.8, 5.2
[J] Edition 4: (1.4), (1.6), Exempel (5.1.8), (5.2)
[J] Edition 6: 1.5, 1.7, Exempel 7.1.8, 7.2

Bemärk, referenser i texten utan parenteser är till [J]ohnsonbaugh Edition 5, referenser i ()-parenteser är till [J] Edition 4, och referenser i []-parenteser är till [J] Edition 6.

Inledning

Någonting är sant men din vän tror det inte. Hur kan du övertala henne att det faktiskt är sant? Först tittar vi på lite logik och då på några olika sätt att bevisa saker. Sista delen av detta block är rekursionsformler. Rekursionsformler är mycket användbara i vanliga livet. Ett exempel där man kan använda en rekursionsformel är följande: hur mycket ränta får jag under tio år om jag sätter in 10.000kr, och räntan ligger på 10% per år?

1. Logik

Läs nu [L] Logik och bevis I av Sarah Norell som handlar om logik.
I texten står några symboler som 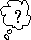och 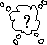. Tanken är att lösa uppgifter som är markerade med 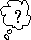själv och då försöka förklara dina svar för andra - det kan ni göra t.ex. via epost, tillsammans eller på forum eller övningar. Om ni vill har ett forum för en mindre grupp är det bara att fråga läraren. Uppgifter eller frågor som markeras med 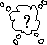är till för att lösa tillsammans och då förklaras som ovan, men tillsammans.

Från detta avsnitt är det viktigaste att du förstår definitioner av t.ex. 'och', 'eller', 'medför', 'om och endast om', 'ekvivalenta', 'icke'. Reglerna i 2.4.1 och 2.5 är viktiga.

Uppgift B5.1
Gör följande uppgifter från [L] Logik och bevis I:
2.1, 2.2.3, 2.3.5, 2.3.6, 2.4.2, 2.5.2, 2.6.1, 2.6.4, 2.6.6, 2.7.2, 2.8.1

2. Bevis

Läs nu [B] Logik och bevis II av Sarah Norell som handlar om bevis.
Den viktigaste delen av detta avsnitt är att kunna förstå ett bevis (= varför någonting är sant), och då bevisa (= förklara på formellt sätt) några exempel. Den största vikten bör läggas på den form av bevis som är det viktigaste för data-ämnet, och det är induktionsbevis. Om man vill kolla eller bevisa att ett program verkligen gör vad man vill, så kan man ofta använda induktion.

Introduktion

Direkt bevis

Uppgift B5.2
Gör följande uppgifter från [B] Logik och bevis II:
3.2.2.1, 3.2.2.2

Uppgift B5.3
Gör övning [J] 1.4.7 (1.4.7) [1.5.13].

Indirekt bevis

Uppgift B5.4
Gör övning [J] 1.4.8 (1.4.8) [1.5.14]

Uppgift B5.5
Gör uppgift 3.3.2.3 från [B] Logik och bevis II.

Om och endast om

Uppgift B5.6
Gör uppgift 3.5.3.2 från [B] Logik och bevis II.

När får man använda exempel som bevis?

Uppgift B5.7
Gör följande uppgifter från [B] Logik och bevis II:
3.6.2, 3.7.2, 3.7.4.2.

Induktion

Uppgift B5.8
Gör uppgift 3.8.5 från [B] Logik och bevis II.

Uppgift B5.9
Gör övning [J] 1.6.19 (1.6.19) [1.7.22].

3. Rekursionsformler

I block 2 lärde vi oss att definiera en följd m.h.a. en rekursionsformel. Läs nu om Example 5.1.8 s. 228-229 (261-262) [Example 7.1.8 s. 283-284] (Towers of Hanoi), och läs  så avsnitt [J] 5.2 (5.2) [7.2]. När du är klar med avsnitt [J] 5.2 (5.2) [7.2] bör kunna lösa linjära homogena rekursionsformler med konstanta koefficienter. -- 'Linjär', 'homogen' och med 'konstanta koefficienter' betyder att  det inte finns ett 'n' i koefficienten framför t.ex. ett a_n i en term och det finns ingen term som ser ut  som a_na_n-1 - se definition 5.2.6 (5.2.6) [7.2.6] på sida 238 (274) [292] i [J].

I exempel 5.2.1 - 5.2.5 (5.2.1 - 5.2.5) [7.2.1 - 7.2.5] i [J] kommer man fram till lösningen med  hjälp av iteration. Avsnittet beskriver hur man kan lösa en speciell typ av rekursionsformel. Exempel 5.2.6 - 5.2.9 (5.2.6 - 5.2.9 ) [7.2.7 - 7.2.9] förklarar vilka rekursionsformler som är av denna speciella typ.

Hur löser man denna typ? Se Exempel 5.2.10 - 5.2.15 (5.2.10 - 5.2.15) [7.2.10 - 7.2.15]:

[J] Exempel 5.2.10 (5.2.10) [7.2.10]

Vi lösar rekursionsformeln definierad av

• Sätt a_n = t ⁿ,   a_n-1 = t ^n-1,   osv. i  (1)  för att få
  tⁿ = 5t ^n-1 + 6t^n-2.        (3)
• Lös (3): t=2, t= 3.
• Lösningen har formen
  a_n = A2 ⁿ + B3ⁿ,         (4) där A och B är konstanter som är beroende av startvärdena.
• Bestäm, med hjälp av (2), A och B:
  • sätt n=0 så 7 = a ₀ = A2⁰ + B3 ⁰ = A + B,
  • sätt n=1 så 16 = a ₁ = A2¹ + B3 ¹ = 2A + 3B.
    Dessa två ekvationer ger A = 5 och B = 2. (Hur? A+B=7 ger A=7-B. Sätt i 16=2A+3B=2(7-B)+3B=14-2B+3B=14+B. Då B=16-14=2, och A=7-B=7-2=5.)
• Sätt A=5 och B=2 i (4), så fås lösningen:
  a_n = 5 2ⁿ + 23ⁿ.

4. Förslag till övningsuppgifter

Uppgifterna i texten ovan.

Övningsuppgifter från [J] 5.2 (5.2) [7.2]:

5.2.1 (5.2.1) [7.2.1], 5.2.3 (5.2.3) [7.2.3], 5.2.6 (5.2.6) [7.2.6], 5.2.16 (5.2.15) [7.2.16],  5.2.20 (5.2.19) [7.2.20], 5.2.22 (5.2.21) [7.2.22]