Referenser utan parenteser är till [J] edition 5, referenser i ()-parenteser är till [J] edition 4, och referenser i []-parenteser är till [J] edition 6.
[J] sida 62-63 (71-72) [85-86]
2. (2.) [2.] B  C = {2,4};
C = {2,4};
3. (3.) [3.] A - B = {7,10};
5. (5.) [5.] 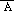 = U - A = {2,3,5,6,8,9};
= U - A = {2,3,5,6,8,9};
6. (6.) [6.] U - C = {1,3,5,7,9,10};
8. (8.) [8.] A
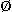 = A= {1,4,7,10};
= A= {1,4,7,10};
9. (9.) [9.] B 
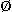 =
=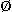 = { };
= { };
11. (11.) [11.] B  U = B = {1,2,3,4,5};
U = B = {1,2,3,4,5};
12. (12.) [12.] A  (B
(B  C) = {1,4,7,10}
C) = {1,4,7,10}  {1,2,3,4,5,6,8}
= {1,4};
{1,2,3,4,5,6,8}
= {1,4};
14. (14.) [14.] (A  B) - C = {1,4} - {2,4,6,8}
= {1};
B) - C = {1,4} - {2,4,6,8}
= {1};
15. (15.) [15.] ( )
)  C = {2,3,5,6,7,8,9,10}
C = {2,3,5,6,7,8,9,10}  {2,4,6,8} =
{2,3,4,5,6,7,8,9,10};
{2,4,6,8} =
{2,3,4,5,6,7,8,9,10};
31. (17.) [32.] X x Y ={(1,a), (2,a), (1,b), (2,b), (1,c), (2,c)};
32. (18.) [33.] Y x X ={(a,1), (a,2), (b,1), (b,2), (c,1), (c,2)};
33. (19.) [34.] X x X ={(1,1), (1,2), (2,1), (2,2)};
34. (20.) [35.] Y x Y ={(a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a),
(c,b), (c,c)};
35. (21.) [36.] X x Y x Z = {(1,a,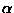 ), (1,a,
), (1,a, 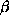 ), (2,a,
), (2,a,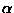 ), (2,a,
), (2,a, 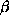 )};
)};
36. (22.) [37.] X x Y x Y = {(1,a,a), (2,a,a)};
37. (23.) [38.] X x X x X = {(1,1,1), (1,1,2), (1,2,1), (1,2,2),
(2,1,1), (2,1,2), (2,2,1), (2,2,2)};
38. (24.) [39.] Y x X x Y x Z = {(a,1,a,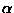 ), (a,1,a,
), (a,1,a, 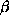 ), (a,2,a,
), (a,2,a,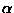 ), (a,2,a,
), (a,2,a, 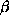 )};
)};
40. (26.) [41.] {{1,2}} och { {1},{2} }
41. (27.) [42.] {{a,b,c}} och { {a,b},{c} } och { {a,c},{b} }
och { {b,c},{a} } och { {a},{b},{c} }
43. (29.) [44.] S
44. (30.) [45.] F
45. (31.) [46.] S
46. (32.) [47.] S
47. (33.) [48.] =
48. (34.) [49.] =
49. (35.) [50.] =
50. (36.) [51.] =
51. (37.) [52.] 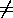
52. (38.) [53.] 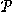 ({a,b}) = {
({a,b}) = {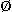 , {a}, {b}, {a,b}},
äkta delmängder är
, {a}, {b}, {a,b}},
äkta delmängder är 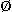 , {a} och {b}
, {a} och {b}
54. (40.) [55.] 210, 210 - 1
55. (41.) [56.] 2n - 1
56. (42.) [57.] X x Y=Y x X  X = Y
X = Y
57. (43.) [58.] F (Rita upp Venn-diagram)
58. (44.) [59.] S (Rita upp Venn-diagram)
59. (45.) [60.] S (Rita upp Venn-diagram)
60. (46.) [61.] F (Rita upp Venn-diagram)
61. (47.) [62.] F (Rita upp Venn-diagram)
62. (48.) [63.] F (Rita upp Venn-diagram)
63. (49.) [64.] F (Rita upp Venn-diagram)
64. (50.) [65.] S
72. (58.) [72.] B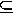 A
A
73. (59.) [73.] 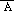 =
= 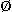 , så A = U
, så A = U
74. (60.) [74.]  =
= 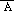

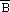 (De Morgan),
så
(De Morgan),
så 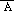
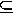
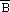 , och darför B
, och darför B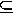 A.
A.
[J] sida 171-172 (203-205) [226-227]:
10. (9.) [10.] 6 x 1=6
12. (11.) [12.] 1 x 6=6
21. (20.) [21.] 1 x 1 x 1 x 1 x 2 x 2 x 2 x 2=24=16
22. (21.) [22.] 1 x 2 x 2 x 2 x 2 x 2 x 2 x 1=26=64
29. (28.) [29.] 4 x 3 x 2 =24
35. (34.) [35.] 5 x 4 x 3 =60
36. (35.) [36.] 1 x 5 x 5 =25
38. (37.) [38.] 4 x 4 x 4 = 43=64
39. (38.) [39.] 4 x 3 x 2 =24
43. (42.) [43.] Här är 200-5+1=196 tal, så 98 är jämna.
44. (43.) [44.] Också 98.
66. (65.) [66.] Strängar som börjar med 100: Välj 0 eller 1 till de övriga 5 positionerna. Ordningen har betydelse och upprepning är tillåten, så det blir 25 möjligheter. Strängar med en 1:a på fjärde positionen: Välj 0 eller 1 till de övriga 7 positionerna. Totalt 27 möjligheter. Antalet strängar som uppfyller båda villkoren, dvs. börjar med 1001 är 24. Totalt får vi alltså 25+ 27- 2 4 strängar m.h.a. PIE.
67. (66.) [67.]
Startar med 1: 27 st., slutar med 1: 27 st., startar och slutar med 1: 26 st., så svaret är27 + 27 - 26 = 28 - 26 = 3(26) strängar.
68. (67.) [68.]
Givet att Ben är ordförande: 5 val av sekreterare och 4 val
av kassör ger (5)(4)=20 val.
Givet att Alice är sekreterare: 5 val av ordförande och 4
val av kassör ger (5)(4)=20 val.
Givet att Alice är sekreterare och Ben är ordförande: 4
val av kassör.
Totalt: 20 + 20 - 4 = 36.
70. (69.) [70.]
Låt E stå för jämn summa och B stå för
att den blå tärningen visar 3. Vi söker |B  E|.
E|.
För det första är |B|=6.
För det andra är |E| = | blå och röd är udda
| + | blå och röd är jämna | = (3)(3)+(3)(3)
= 18.
För det tredje är |E  B|=3. Så
B|=3. Så
|B  E| = |B|+|E|- |E
E| = |B|+|E|- |E  B| = 6 + 18 - 3 = 21.
B| = 6 + 18 - 3 = 21.
[J] sida 182-184 (220-224) [237-239] :
2. (2.) [2.]
abcd, abdc, acbd, acdb, adcb, adbc, bacd, bacd, bcad, bcda, bdac, bdca,
cabd, cadb, cbad, cbda, cdab, cdba, dabc, dacb, dbac, dbca, dcab, dcba.
3. (3.) [3.] 4*3*2=24
5. (5.) [5.] 11!=P(11,11)
6. (6.) [6.] 11*10*9*8*7=P(11,5)
8. (8.) [8.] 12*11*10*9=P(12,4)
10. (10.) [10.] Räkna X='ACE' som en bokstav, och ordna de tre 'bokstäverna' X, B, D. Det blir 3! sätt.
11. (11.) [11.] För varje ordning i uppgift 10 finns det 3! ordningar av ACE, så totalt blir det 3!*3! strängar.
12. (12.) [12.] Räkna X=DB och Y=AE som bokstäver. Det finns då tre bokstäver som ska ordnas, så det finns 3! sätt.
15. (15.) [15.]
Innehåller AB: 4! strängar.
Innehåller CD: 4! strängar.
Innehåller båda: 3! strängar. Antalet strängar som innehåller AB eller CD är då
4! + 4! - 3! = 42. Antalet som varken innehåller AB eller CD är 5! - 42 = 78.
16. (16.) [16.]
Innehåller AB: 4! strängar.
Innehåller BE: 4! strängar.
Innehåller båda som ABE: 3! strängar. Antalet strängar som innehåller minst en av AB och BE är
4! + 4! - 3! = 42. Antalet som inte innehåller någon av dem är
5! - 42
= 78.
20. (20.) [20.] First arrange the Vesuvians and the Jovians (10+8=18 people) in a line: 18! ways. A Martian can stand in any position between the others or at the two ends of the line, that is in any one of 19 positions. There are thus P(19,5) ways of arranging the Martians. So by the multiplication principle the answer is 18! P(19,5).
26. (26.) [26.] abc, abd, acd, bcd
Extra övningsuppgifter till Venn-diagram i läsanvisningen:
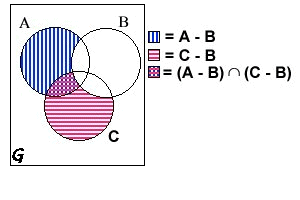
1. 
2. 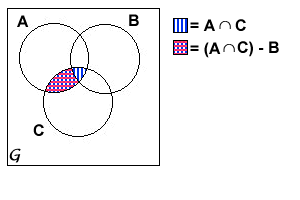
3. De två Venn-diagram är likadana, så de två mängderna
(A-B)  (C-B) och (A
(C-B) och (A
 B)-B är lika.
B)-B är lika.
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
