 |
MA014G |
Referenser utan parenteser är till [J] edition 5, referenser i ()-parenteser är till [J] edition 4, och referenser i []-parenteser är till [J] edition 6.
Uppgifter i läsanvisningen
Uppgift B3.1
T.ex. 3 = (-6)3 +(3)7;7 = (-14)3 + (7)7;
0 = (7)3 + (-3)7;
-7 = (14)3 + (-7)7;
40= (-80)3 + (40)7.
Uppgift B3.2
(a) { -12, -11, -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12};(b) { -12, -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, 12};
(c) { -12, -9, -6, -3, 0, 3, 6, 9, 12}.
Uppgift B3.3
(a) sgd(3,7) = 1, så L= {1x | x
} = ;
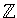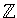(b) sgd(4,6) = 2, så L= {2x | x
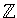} = {0, 
2,
4, 6, .
. . };
(c) sgd(6,9) = 3, så L= {3x | x
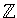} = {0, 3,
6, 9, .
. . }.
Extra övningsuppgifter i linjärkombinationer och aritmetikens fundamentalsats
(a) I ett av ovanstående exempel fann vi att sgd(15939, 9367) =1 med hjälp av Euklides algoritm, som vi nu skriver om:
15939 = 9367(1) + 6572 ==>
6572 = 15939 - 9367(1)
9367 = 6572(1) + 2795 ==>
2795 = 9367 - 6572(1)
6572 = 2795(2) + 982
==> 982 =
6572 - 2795(2)
2795 = 982(2) + 831
==> 831 =
2795 - 982(2)
982 = 831(1) + 151
==> 151 =
982 - 831(1)
831 = 151(5) + 76
==>
76 = 831 - 151(5)
151 = 76(1) + 75
==> 75
= 151 - 76(1)
76 = 75(1) +
1 ==>
1 = 76 -
75(1)
75 = 1(75)
Vi börjar med den 8:e ekvationen, som uttrycker sgd(15939, 9367) =1 som en linjärkombination av 76 och 75. Därnäst substituerar vi den 7:e ekvationen in i uttrycket, förenklar det, substituerar sedan den 6:e ekvationen in i uttrycket, förenklar igen, etc. :
1 = 76 - 75(1)
= 76 -[151 - 76(1)](1) [här substituerar vi in 7:e ekvationen]
= 76(2) - 151(1) [förenkling ] [Koll: HL =152 - 151 = 1]
= [831 - 151(5)](2) -151(1) [här substituerar vi in 6:e ekvationen ]
= 831(2) -151(11) [förenkling ] [Koll: HL =1662 - 1661 = 1]
= 831(2) -[982 - 831(1)](11) [här substituerar vi in 5:e ekvationen]
= 831(13) -982(11) [förenkling ] [Koll: HL =10803 - 10802 = 1]
= [2795 - 982(2)](13) -982(11) [här substituerar vi in 4:e ekvationen]
= 2795(13) -982(37) [förenkling ] [Koll: HL =36335 - 36334 = 1]
= 2795(13) -[6572 - 2795(2)](37) [här substituerar vi in 3: ekvationen]
= 2795(87) -6572(37) [förenkling ] [Koll: HL =243165 - 243164 = 1]
= [9367 - 6572(1)](87) -6572(37) [här substituerar vi in 2: ekvationen]
= 9367(87) -6572(124) [förenkling ] [Koll: HL =814929 - 814928 = 1]
= 9367(87) -[15939 - 9367(1)](124) [här substituerar vi in 1: ekvationen]
= 9367(211) -15939(124) [förenkling ] [Koll: HL =1976437 - 1976436 = 1]
Från den sista ekvationen fås nu, att 1 = 15939a + 9367b, där a = -124 och b = 211.
(b) Ur (a) fås 1 = 9367(211) -15939(124), så
(c) 100 = 9367(21100) +15939(-12400).
(d) 60 = 1 x 2 x 2 x 3 x 5, där enheten är 1.
(e) -60 = (-1) x 2 x 2 x 3 x 5, där enheten är -1.
(f) -3 = (-1) x 3, där enheten är -1.
[J] sida 131 (156-157) [213]:
1. (7.) [1.]
90 = 60(1) + 30;
60 = 30(2),
så sgd(90,60) =30.
2. (8.) [2.]
273 = 110(2) +53;
110 = 53(2) + 4;
53 = 4(13) +1
;
4 =
1(4),
så sgd(273,110)=1.
3. (9.) [3.]
1400 = 220(6) +80;
220 = 80(2) +60;
80 = 60(1) +
20;
60 = 20(3),
så sgd(1400,220)=20.
4. (10.) [4.]
825 = 315(2) +195;
315 = 195(1) +120;
195 = 120(1) + 75;
120 = 75(1) + 45;
75 = 45(1) +
30;
45 = 30(1)
+ 15;
30 = 15(2),
så sgd(825,315)=15.
5. (11.) [5.] sgd(20,40) =20, eftersom 20 | 40.
6. (12.) [6.] sgd(331,993) =331, eftersom 331 | 993.
7. (13.) [7.]
4807 = 2091(2) + 625;
2091 = 625(3) + 216;
625 = 216(2) + 193;
216 = 193(1) +
23;
193 = 23(8)
+ 9;
23 =
9(2) + 5;
9 =
5(1) + 4;
5 =
4(1) + 1;
4 =
1(4),
så sgd(4807, 2091)=1.
8. (14.) [8.] sgd(2475, 32670) = 495.
9. (15.) [9.] sgd (67942, 4209) = 23.
18. (22.) [11.]
Nr. 1: (7:) [1:]
30 = 90(1) + (60)(-1)
Nr. 2: (8:) [2:]
273 = 110(2) +53 ==> 53 =
273 -110(2)
110 = 53(2) + 4 ==>
4 = 110 - 53(2)
53 = 4(13) +1 ==>
1 = 53 - 4(13).
Därav fås
1 = 53 - 4(13)
= 53 - [110 - 53(2)](13)
= 53(27) -110(13)
= [273 -110(2)](27) -110(13)
= 273(27) + 110(-67).
Nr. 3: (9:) [3:]
1400 = 220(6) + 80
==> 80 = 1400 - 220(6)
220 = 80(2) + 60
==> 60 = 220 - 80(2)
80 = 60(1) + 20
==> 20 = 80 - 60(1)
Därav fås
20 = 80 - 60
= 80 - [220 - 80(2)]
= 80(3) - 220
= [1400 - 220(6)](3) - 220
= 1400(3) +220(-19).
Nr. 4: (10:) [4:]
15 = 45 - 30
= 45 -[75-45]
= 45(2) - 75
= [120-75](2) -75
= 120(2) -[195-120](3)
= [315-195](5) - 195(3)
= 315(5) -195(8)
= 315(5) -[825-315(2)](8)
= 825(-8) + 315(21).
Nr. 7: (13:) [7:]
1 = 5 - 4
= 5 - [9-5]
= 5(2) -9
=[23-9(2)](2) -9
= 23(2) - 9(5)
= 23(2) - [193 - 23(8)](5)
= 23(42) -193(5)
= [216 -193](42) -193(5)
= 216(42) -193(47)
= 216(42) -[625 -216(2)](47)
= 216(136) - 625(47)
= [2091 -625(3)](136) - 625(47)
= 2091(136) - [4807 - 2091(2)](455)
= 4807(-455) + 2091(1046).
[J] sida 137 (163-165) [179]
5. (5.) [finns ej] sgd(55,20) = 5
21. (14.) [18.]
Antalet kaninpar efter ett
år = antalet kaninpar efter 12 månader, så det är a12 vi skal
räkna ut här. Därför har vi
| a0 | = | 1 | ||||
| a1 | = | 1 | ||||
| a2 | = | a1 + a0 | = | 1 + 1 | = | 2 |
| a3 | = | a2 + a1 | = | 2 + 1 | = | 3 |
| a4 | = | a3 + a2 | = | 3 + 2 | = | 5 |
| a5 | = | a4 + a3 | = | 5 + 3 | = | 8 |
| a6 | = | a5 + a4 | = | 8 + 5 | = | 13 |
| a7 | = | a6 + a5 | = | 13 + 8 | = | 21 |
| a8 | = | a7 + a6 | = | 21 + 13 | = | 34 |
| a9 | = | a8 + a7 | = | 34 + 21 | = | 55 |
| a10 | = | a9 + a8 | = | 55 + 34 | = | 89 |
| a11 | = | a10 + a9 | = | 89 + 55 | = | 144 |
| a12 | = | a11 + a10 | = | 144 + 89 | = | 233 |
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden