Referenser utan parenteser är till [J] edition 5, referenser i ()-parenteser är till [J] edition 4, och referenser i []-parenteser är till [J] edition 6.
Uppgifter i läsanvisningen
Uppgift B4.1
- Sant, 81 - 1 = 80 = 8(10)
- Sant, 81 - 1 = 8(10)
- Falskt, 112 - 4 = 108
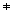 k(11) för varje
heltal k
k(11) för varje
heltal k
- Sant, 1000 - (-1) = 1001 = 13(77)
- Falskt, 9 - 90 = -81
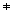 k(5) för alla heltal k.
k(5) för alla heltal k.
- Sant 937-37=900=9(100).
- Falskt, Med t.ex. a=937, b=37 och m=100 har vi
937
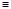 37 (mod 100) men 937 = 37 är falskt.
37 (mod 100) men 937 = 37 är falskt.
- Sant, Om a
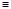 b (mod m), så finns
ett heltal k så att a-b=km. Addera och subtrahera c till vänster led:
b (mod m), så finns
ett heltal k så att a-b=km. Addera och subtrahera c till vänster led:
a+c-(b+c)=km, d.v.s. a+c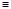 b+c (mod m).
b+c (mod m).
- Sant. Om a
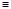 b (mod m), så finns
ett heltal k så att a-b=km. Multiplicera båda sidor med c:
b (mod m), så finns
ett heltal k så att a-b=km. Multiplicera båda sidor med c:
ac-bc=kmc=(kc)m, d.v.s. ac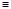 bc (mod m).
bc (mod m).
Uppgift B4.2
{x| x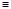 3 (mod 5)}={x | x-3 = k(5),
k
3 (mod 5)}={x | x-3 = k(5),
k 
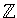 }={..., -12, -7, -2, 3, 8, 13, 18, ...}.
}={..., -12, -7, -2, 3, 8, 13, 18, ...}.
Uppgift B4.3
Multiplikationstabellen för Z2 är:
 |
|
|
|
|
|
|
|
|
|
|
Multiplikationstabellen för Z3 är:
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Multiplikationstabellen för Z6 är:
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Multiplikationstabellen för Z7 är:
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Multiplikationstabellen för Z8 är:
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Multiplikationstabellen för Z9 är:
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uppgift B4.4
De tal x {0, 1, 2, ... , 9} sådana
att sgd(x,10) = 1 är 1, 3, 7 och 9.
{0, 1, 2, ... , 9} sådana
att sgd(x,10) = 1 är 1, 3, 7 och 9.a och b kan t.ex. väljas enligt 1=(-9)1+(1)10,
1=(-3)3+(1)10,
1=(3)7+(-2)10 och
1=(-1)9+(1)10.
[-9]=[1] så [1]
 [1]= [1].
[1]= [1].[-3]=[7] så [3]
 [7]= [1].
[7]= [1].Med 1=(3)7+(-2)10 ser vi direkt att [3]
 [7]= [1].
[7]= [1].[-1]=[9] så [9]
 [9]= [1].
[9]= [1].
Uppgift B4.5
(a) Med Euklides algoritm:12=2(5)+2.
5=2(2)+1, så
1=5-2(2)=5-(12-2(5))(2)=5(5)-2(12).
Det innebär att [5]
 [5]=[1] och den multiplikativa inversen till [5] är [5] i Z12.
[5]=[1] och den multiplikativa inversen till [5] är [5] i Z12.
(b) Använd Euklides algoritm:
31=22(1)+9.
22=9(2)+4.
9=4(2)+1 så
1=9-4(2)=9-(22-9(2))(2)=(5)9-(2)22=(5)(31-22)-(2)22=(5)31+(-7)22.
[-7]=[24] så inversen till [22] i Z31 är [24].
(c) Inversen är [7].
(d) Inversen är [9].
Uppgift B4.6
Antag att [x] har en multiplikativ invers [z]. [x] är nolldelare så det finns [y]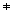 [0] så att
[x]
[0] så att
[x] [y]=[0]. Multiplicera båda sidor med
inversen [z] till [x]; [z]
[y]=[0]. Multiplicera båda sidor med
inversen [z] till [x]; [z] [x]
[x]
 [y]=[z]
[y]=[z] [0]=[0]. [z]
[0]=[0]. [z] [x]=[1] så vi får att [y]=[0]. Det är en
motsägelse. Alltså kan inte [x] ha någon invers.
[x]=[1] så vi får att [y]=[0]. Det är en
motsägelse. Alltså kan inte [x] ha någon invers.
Uppgift B4.7
Antag att det finns två inverser [y] och [z] till [x]. Att de är inverser till [x] innebär att [x] [y]=[1]=[x]
[y]=[1]=[x] [z] och multiplicerar vi denna likhet med [y] från vänster får vi
att [y]
[z] och multiplicerar vi denna likhet med [y] från vänster får vi
att [y] [x]
[x]
 [y]=
[y]
[y]=
[y] [x]
[x]
 [z]. [y] är invers till [x] så
[y]
[z]. [y] är invers till [x] så
[y] [x]=[1] så likheten tidigare är
[1]
[x]=[1] så likheten tidigare är
[1]
 [y]=
[1]
[y]=
[1] [z] ur vilken det följer att [y]=[z].
D.v.s. inversen måste vara unik.
[z] ur vilken det följer att [y]=[z].
D.v.s. inversen måste vara unik.
Uppgift B4.8
Att ax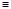 1 (mod n) innebär
att det finns ett heltal k så att ax-1=kn. Multipliceras båda sidor om likhetstecknet med b får vi att abx-b=bkn. Produkten bk är ett heltal så
a(bx)
1 (mod n) innebär
att det finns ett heltal k så att ax-1=kn. Multipliceras båda sidor om likhetstecknet med b får vi att abx-b=bkn. Produkten bk är ett heltal så
a(bx) 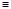 b
( mod n).
b
( mod n).
Uppgift B4.9
Med uppgift B4.5(a) får vi att x=5 är en lösning till kongruensen 5x
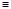 1 (mod 12).
Enligt uppgift B4.8 är då x=5(4)=20 en lösning
till kongruensen 5x
1 (mod 12).
Enligt uppgift B4.8 är då x=5(4)=20 en lösning
till kongruensen 5x 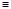 4 (mod 12).
4 (mod 12).
Uppgift B4.10
(a) Använd sats B4.9 med a=10, n=12 och b=6.
sgd(10,12)=2 och 2|6 så satsen säger att det finns två lösningar i Z12 och de ges av [x]=[3x0+t6] med t=0,1 och där x0
 {0,1,2,3,4,5} är en lösning till
5x
{0,1,2,3,4,5} är en lösning till
5x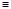 1(mod 6). x0=5 fungerar. Med t=0 fås [15] och med t=1 fås [21]. D.v.s. [3] och [9] är lösningarna till
[10]
1(mod 6). x0=5 fungerar. Med t=0 fås [15] och med t=1 fås [21]. D.v.s. [3] och [9] är lösningarna till
[10]  [x] = [6] i Z12.
[x] = [6] i Z12.
(b) Talet x

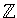 är en lösning till
kongruensen 10x
är en lösning till
kongruensen 10x
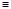 6 (mod 12) om och endast om
[10]
6 (mod 12) om och endast om
[10]  [x] = [6] i Z12
(Varför?).
Ur deluppgift a) får vi då att x är en lösning om och endast om
x finns i en av kongruensklasserna [3]12 eller [9]12.
[x] = [6] i Z12
(Varför?).
Ur deluppgift a) får vi då att x är en lösning om och endast om
x finns i en av kongruensklasserna [3]12 eller [9]12.
Uppgift B4.11
(a) Använd Euklides algoritm:
37=2(14)+9.
14=1(9)+5.
9=2(5)-1 så
1=2(5)-9=2(14-9)-9=2(14)-3(9)=2(14)-3(37-2(14))=8(14)-3(37).
Inversen till [14] i Z37 är alltså [8].
(b) Med deluppgift (a) kan man komma fram till att x0=8 (varför?).
(c) (i) Observera först att ett heltal x löser kongruensen
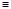 15
(mod 111)
15
(mod 111) 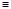 5
(mod 37).
5
(mod 37).( Om x är ett tal sådant att 42x
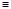 15 (mod 111) så finns ett k så att 42x-15=111k. Delar vi båda leden med
3 så blir resultatet likheten 14x-5=37k vilket betyder att
14x
15 (mod 111) så finns ett k så att 42x-15=111k. Delar vi båda leden med
3 så blir resultatet likheten 14x-5=37k vilket betyder att
14x 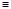 5
(mod 37). Andra riktningen: om x är ett tal sådant att
14x
5
(mod 37). Andra riktningen: om x är ett tal sådant att
14x 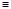 5 (mod 37)
så finns ett k så att 14x-5=37k. Multipliceras båda sidor med 3 så har vi att
42x-15=111k vilket innebär att
42x
5 (mod 37)
så finns ett k så att 14x-5=37k. Multipliceras båda sidor med 3 så har vi att
42x-15=111k vilket innebär att
42x 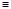 15
(mod 111).)
15
(mod 111).)Använd sats B4.10 med a=14, b=5 och n=37:
sgd(14,37)=1 och 1|5 så [14]
 [x]=[5]
har én lösning i Z37. Denna ges av sats B4.10 också, men
vi kan hitta den utan:
[x]=[5]
har én lösning i Z37. Denna ges av sats B4.10 också, men
vi kan hitta den utan:Vi har
 [x]=[5].
[x]=[5].Multiplicera båda sidor med [8] (multiplikativa inversen till [14] enligt (a)), dvs.
 [14]
[14]  [x] =
[8]
[x] =
[8]  [5],
[5], [x] =
[40],
[x] =
[40], [x]=[5].
[x]=[5]. Talet x löser då kongruensen 42x
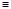 15
(mod 111) om och endast om
x
15
(mod 111) om och endast om
x  [3]37 = {...,-34, 3, 40, 77, ...}.
[3]37 = {...,-34, 3, 40, 77, ...}. Observera att [3]37 = [3]111
 [40]111
[40]111
 [77]111, högersiden är
lösningen som ges av sats B4.10.
[77]111, högersiden är
lösningen som ges av sats B4.10.
(ii) sgd(111,42)=3 och 3 delar inte 25 så ekvationen [42]
 [x]=[25] har enligt sats B4.10
ingen lösning i Z111.
Det innebär att det inte finns något heltal x som
löser kongruensen
42x
[x]=[25] har enligt sats B4.10
ingen lösning i Z111.
Det innebär att det inte finns något heltal x som
löser kongruensen
42x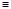 25 (mod 111).
25 (mod 111).
The author would like to thank the following for their contribution
to various updates of the original manuscript:
Pia Heidtmann.
© Andreas Brodin
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
Updated 070811
