[L]2.2.3 Negation
Bestäm negationen av följande påståenden.
[L]2.3.6 Och, eller
Låt p vara påståendet "5<3", låt q vara påståendet "En vecka innehåller precis 6 dagar" och låt r vara påståendet "Alla häster är bruna". Bestäm om följande påståenden är sanna eller falska.
[L]2.4.2 Sanningstabeller
[L]2.4.5 Ekvivalenta påståenden
Skriv, med hjälp av reglarna i avsnitt 2.4.3 och definitioner av "och" och "eller", följande på så enkelt sätt som möjligt. Om ett påståendet är en tautologi, skriva att det är ekvivalent med T, en allmän tautologi. Om det är ekvivlanent med en motsägelse, skriva att det är ekvivalent med M, en allmän mötsägelse.Kontrollera, med hjälp av sanningstabeller, att dina svar är ekvivalent med de ursprungliga påståendena.
[L]2.5.2 Ekvivalent
Förenkla följande påståenden. Förklara vilka lagar som du använder i varje steg. Kontrollera, med hjälp av sanningstabeller, dina svar.[L]2.6.4 Implikation
[L]2.8.1 För alla, det existerar
[J] Uppgift 1.4.8 (1.4.8) [1.5.14]
Bevis:| 1 | Anta att xy=0, x 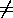 0 och y 0 och y
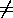 0. 0. |
Antagandet |
| 2 | x 0 =0 0 =0 |
Från [J] uppgift 1.4.7 (1.4.7) [1.5.13] |
| 3 | xy=x 0 0 |
Båda xy och x 0 är
lika med 0, och är därför lika med varandra. 0 är
lika med 0, och är därför lika med varandra. |
| 4 | y=0 | Steg 1 och 3 och satsen i uppgiften. |
[J] Uppgift 1.6.9 (1.6.9) [1.7.9]
Ledtråd
- Induktionsbas. Sätt i n=1.
VL = 1
22 - 1HL = 3
4- 1
2(1+1)- 1
2(1+2)= 3
4- 1
4- 1
6=
18
24- 6
24- 4
24= 8
24= 1
3 - Induktionssteg
- Anta att påståendet är sant för n=1,2,...,k.
För n=k har vi så att
1
22-1+ 1
32-1+ ... + 1
(k+1)2-1= 3
4- 1
2(k+1)- 1
2(k+2)gäller. - Visa nu att påståendet är sant för n=k+1,
dvs visa att
Betrakta:1
22-1+ 1
32-1+ ... + 1
(k+1)2-1+ 1
(k+1+1)2-1= 3
4- 1
2(k+1+1)- 1
2(k+1+2)gäller. 1
22-1+ 1
32-1+ ... + 1
(k+1)2-1+ 1
(k+1+1)2-1= 3
4- 1
2(k+1)- 1
2(k+2)+ 1
(k+2)2-1= 3
4- 1
2(k+2)- 1
2(k+1)+ 1
k2+4k+3= 3
4- 1
2(k+2)- 1
2(k+1)+ 1
(k+1)(k+3)= 3
4- 1
2(k+2)- k+3
2(k+1)(k+3)+ 2
2(k+1)(k+3)= 3
4- 1
2(k+2)- k+3-2
2(k+1)(k+3)= 3
4- 1
2(k+2)- k+1
2(k+1)(k+3)= 3
4- 1
2(k+2)- 1
2(k+3)= 3
4- 1
2(k+1+1)- 1
2(k+1+2)
- Anta att påståendet är sant för n=1,2,...,k.
För n=k har vi så att
- Slutsats
[J] Uppgift 1.6.19 (1.6.19) [1.7.22]
Ledtråd
- Induktionsbas. Sätt i n=1. 111 - 6 = 5 är delbart med 5.
- Induktionssteg
- Anta att påståendet är sant för n=1,2,...,k.
Så har vi t.ex. för n=k att 11k - 6 är delbart
med 5.
Vi kan skriva 11k - 6 = 5s för något heltal s. - Betrakta 11k+1 - 1.
11k+1 - 1 = 11 11k - 1 = 11(11k - 1) + 11
- 1 =11(5s) + 10=5(11s + 2), som är delbart med 5.
11k - 1 = 11(11k - 1) + 11
- 1 =11(5s) + 10=5(11s + 2), som är delbart med 5.
- Anta att påståendet är sant för n=1,2,...,k.
Så har vi t.ex. för n=k att 11k - 6 är delbart
med 5.
- Slutsats
Uppgifter från [J]5.2 (5.2) [7.2]
3 (3) [3]
Icke linjärt homogen med konstanta koefficienter eftersom koefficienten framför an-1 är 2n som inte är konstant.
6 (6) [6]
Icke linjärt homogen med konstanta koefficienter ty det finns termen 1.
16 (15) [16]
- Lös t2 - 7t + 10 = 0. Rötterna är t = 2 och t = 5.
- Så an=A2n+B5n, konstanter A och B.
- Bestäm, med hjälp av startvillkoren, A och B. A = 3 och B = 2.
- Lösningen är an=3
 2
n + 2
2
n + 2 5n.
5n.
20 (19) [20]
- Lös t2 - 6t + 9 = 0. Rötterna är t = -3 (två gånger)
- Så an=3n(A+Bn), konstanter A och B.
- Bestäm, med hjälp av startvillkoren, A och B.
För n = 0: 1 = A, och
för n=1: 1=3(A+B)=3(1+B) så B=-2/3. - Lösningen är an = 3n(1 - (2n/3) ) =
3n - 2n
 3n - 1.
3n - 1.
22 (21) [22]
- Lös 9t2 - 6t + 1=0. Rötterna är t=1/3 (två gånger)
- Så an=(1/3)n(A+Bn), konstanter A och B.
- Bestäm, med hjälp av startvillkoren, A och B.
För n=0: 6=A, och
för n=1: 5=(1/3)(6+B)=2+(B/3), så B=9. - Lösningen är an=(1/3)n(6 + 9n)
The author would like to thank the following for their contribution
to various updates of the original manuscript:
Katharina Huber, Fredrik Ståhl, Sam Lodin and Pia Heidtmann.
© Sarah Norell
c/o Pia Heidtmann
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
c/o Pia Heidtmann
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
Updated 070811
