Referenser utan parenteser är till [J] edition 5, referenser i ()-parenteser är till [J] edition 4, och referenser i []-parenteser är till [J] edition 6.
Uppgifter i läsanvisningen
Uppgift B6.1 - B6.4
[J] Section 6.1 (6.1) [8.1]:
6 (2) [6].
The edge ab must be included, so we
start with it. Now we have a choice: bc or bd. If we take bc we are left
with the edge bd, which we have to take at some point. When we do take
it, we will find ourselves stuck at b with no edge remaining by which to
leave b. So we cannot take bc. If instead we take bd, we find we have the
same problem, this time with bc remaining.
7 (3) [7].
We will have exactly the same problem
as in exercise 6 (2) [6]. When we go through b we use up two edges, so
we can go through it twice, but when we visit it the third time, we use the last edge and cannot leave again.
9 (5) [9]. abdefcebca
10 (6) [10]. abcfihfehgecgdebda
11 (7) [11]. Not simple as it contains both a loop (e5) and parallel edges (e1 and e6 ). e1 is incident on v1 and v2.
12 (8) [12]. Simple graph. e1 is incident on v2 and v4.
13 (9) [13]. Simple graph. There is no e1 .
14 (10) [14]. 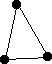 K3
K3 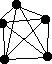 K5
K5
15 (11) [15]. n(n-1)/2.
16 (12) [16]. K3,3 - see solution to exercise 20 (16) [24] in [J].
18 (14) [18]. Bipartite. V1={v 1, v6, v3, v4, v8, v 10, v9} V2={v5, v2, v 7}
19 (15) [19]. Bipartite. V1={Gre, Buf, Dou, Sho, Mud} V2={She, Wor, Cas, Lan, Gil}
21 (17) [21]. Not bipartite as it contains a triangle, v1v2v3v1.
22 (18) [22]. See 21 (17) [21] .
25 (21) [25]. mn
Uppgift B6.5
1,2,5,6,2,1 är en stig från 1 till 1, men den är inte enkel.
1,2,5,7 är inte en stig, ty det finns ingen kant (5,7) i grafen.
Uppgift B6.6 - B6.7
[J] Section 6.2 (6.2) [8.2]:
2 (2) [2]. simple path
3 (3) [3]. none
5 (5) [5]. none
6 (6) [6]. cycle
8 (8) [8]. simple path
9 (9) [9]. simple path
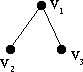
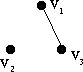
12 (12) [12].
26 (26) [26].
 |
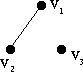 |
 |
 |
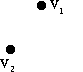 |
 |
 |
 |
 |
 |
 |
 |
29 (29) [29]. Has an Eulerian cycle as all degrees are even.
30 (30) [30]. No Eulerian cycle as v3 has odd degree.
32 (32) [32]. abdcbfgjfejhcideiha
33 (33) [33]. abcdehfijkihgfegdca
35 (35) [35]. when n is odd
36 (36) [36]. both m and n must be even
Uppgift B6.8
[J] Section 6.3 (6.3) [8.3]:
2 (2) [2]. abcdefnpmlkjoihga
4 (4) [4]. This graph is bipartite, with an uneven partition of the vertices so it is not Hamiltonian.
5 (5) [5]. The edges gi, ij, fg, gh and jg would all have to be included, which would lead to g being used too many times.
7 (7) [7]. abcglmrqpkjfeinotshda
8 (8) [8].
We can only use 2 edges at c, 2 at e and 2 at f so we don't use 2 edges
at c, 1 edge at d and 3 edges at e leaving a total of 6 edges which is too
few for a hamilton cycle.
10 (10) [10]. K3
11 (11) [11]. K5
Uppgift B6.9
[J] Section 6.4 (6.4) [8.4]:
2 (2) [2]. 11 abcg
3 (3) [3]. 10 abcdz
5 (5) [5]. 10 hfcd
Uppgift B6.10
[J] Section 6.5 (6.5) [8.5]:
2 (2) [2].
| a | b | c | d | e | f | g | |||
 |
 |
||||||||
| a | 0 | 2 | 0 | 0 | 0 | 0 | 0 | ||
| b | 2 | 0 | 1 | 0 | 1 | 0 | 0 | ||
| c | 0 | 1 | 2 | 0 | 1 | 0 | 0 | ||
| d | 0 | 0 | 0 | 2 | 1 | 0 | 1 | ||
| e | 0 | 1 | 1 | 1 | 0 | 1 | 0 | ||
| f | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ||
| g | 0 | 0 | 0 | 1 | 0 | 1 | 0 | ||
8 (8) [8].
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | |||
 |
 |
|||||||||||
| a | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| b | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| c | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| d | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | ||
| e | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | ||
| f | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| g | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | ||
Uppgift B6.11
[J] Section 6.6 (6.6) [8.6]:
2 (2) [2].
Isomorphic, as there is a bijection f from the vertices of G1
to the vertices of G2 which preserves the edges. f is defined
by f(a)=a', f(b)=c', f(c)=e', f(d)=g', f(e)=b', f(f)=d', f(g)=f'.
3 (3) [3].
These are not isomorphic. Choose ONE of the following to show this:
- G1 contains triangles (such as abca) whereas G2 contains no triangles.
- The vertices of G2 cannot be coloured with 2 colours so that no two adjacent vertices are coloured with the same colour. G2 can be coloured with 2 colours.
- G2 is bipartite whereas G1 is not.
- The complement of G1 consists of one component whereas the complement of G2 consists of two.
note that giving a failed attempt to pair up the vertices is never enough to show that two graphs are non-isomorphic unless you have tried every possible way to pair them up - that is, in this case all 6! = 720 ways.
5 (5) [5].
Isomorphic, as there is a bijection f from the vertices of G1
to the vertices of G2 which preserves the edges. f is defined
by f(a)=b', f(b)=d', f(c)=e', f(d)=a', f(e)=c'.
6 (6) [6].
Here is a description of how I
solved this problem. Note that such a description would not usually be included in an answer
given to a question of this kind, one would just give the 'answer' below. First, I wrote the degree of each vertex next to
the vertex in the graph, and then compared the vertices of each degree. There
are two vertices of degree 5 in each graph, and as G2 is symmetrical,
it doesn't matter which way we pair them up. Take f(l)=l' and f(k)=k'. Now
there are two vertices of degree 4 adjacent to both l and l'. Try pairing
those (might be wrong - we'll see): f(a)=a', f(h)=d'. Now k is adjacent to
two vertices of degree 4, namely, e and d, where d is adjacent to a. Similarly
k' is adjacent to c' and b' where b' is adjacent to f(a)=a'. To preserve
the edges, we pair d and b' so f(d)=b', leaving f(e)=c'. Now I look for
vertices which are adjacent to those I have already paired up. g is adjacent
to both l and h, and h' is adjacent to both f(l)=l' and f(h)=d' so f(g)=h'.
f is adjacent to g,k,e and g' is adjacent to f(g)=h', f(k)=k' and f(e)=c'
so f(f)=g'. Only one of the neighbours of a is not paired and that is b.
Similarly, of the neighbours of f(a)=a', only e' is unpaired so f(b)=e'.
c is adjacent to both b and d and f' is adjacent to both f(b)=e' and f(d)=b'
so f(c)=f'. We are left we just i and j and i' and j'. By comparing neighbours,
we see f(i)=i' and f(j)=j'. Now for the 'answer' to the question:
G1 and G2 are isomorphic because there is a bijection f mapping the vertices of G1 to G2 so that there is an edge uv in G1 if and only if the corresponding edge f(a)f(b) is present in G2. The function f is defined as follows: f(a)=a', f(b)=e', f(c)=f', f(d)=b', f(e)=c', f(f)=g', f(g)=h', f(h)=d', f(i)=i', f(j)=j', f(k)=k', f(l)=l'.
8 (8) [8].
Hint: look at the vertices of degree 3.
9 (9) [9].
First I looked at the degrees. It didn't help. Next I looked at the
complements. Did not look too nice, so I decided to come back to that later
if I could not find anything else. Then I noticed that in both graphs the
only vertex of degree 4 is contained in two triangles in G1 and
just one triangle in G2.
G1 and G2 are not isomorphic because (chose any ONE of the following)
- the only vertex e of degree 4 in G1 is contained in two triangles abe and efg, whereas the only vertex f' of degree 4 in G2 is contained in just one triangle f'g'e'.
- if we remove the vertices of degree 4 from G1 and from G2, one of the remaining graphs can be coloured with 2 colours whereas the other can not.
- G1 contains two triangles whereas G2 contains only one.
Uppgift B6.12
[J] Section 7.1 (7.1) [9.1]:
9 (2) [9].
Answer 4
10 (4) [10].
Answer 5
Uppgift B6.13
[J] Section 7.2 (7.2) [9.2]:
2 (2) [2]. Aphrodite, Uranus.
3 (3) [3]. Aphrodite, Kronos, Atlas, Prometheus.
5 (5) [5]. Zeus, Poseidon, Hades.
6 (6) [6]. One edge drawn vertically with Aphrodite as root and Eros as leaf.
24 (24) [24]. No such graph exists. A terminal node (leaf) has degree one.
26 (26) [26]. The root has degree three and each child of the root is adjacent to two leaves.
Uppgift B6.14
[J] Uppgift 7.3.9 (7.3.9) [9.3.9]:
The edges in the spanning tree are (a,c), (b,c), (c,d), (d,f), (f,e), (f,g), (f,h), (f,i).
Uppgift B6.15
[J] Section 7.4 (7.4) [9.4]:
2 (2) [2].
The edges in the minimal spanning tree are (1,2), (2,3), (3,6), (6,9),
(2,5), (5,8), (8,7), (7,4).
3 (3) [3].
The edges in the minimal spanning tree are (4,1), (1,2), (2,5), (5,6),
(6,3).
5 (5) [5].
The edges in the minimal spanning tree are
(1,2), (2,5), (2,7), (3,7),
(4,8), (5,6), (5,9), (6,15), (7,11), (8,12), (9,10), (10,13), (11,14), (12,16),
(15,16).
The authors would like to thank the following for their contribution
to various updates of the original manuscript:
Pia Heidtmann.
c/o Pia Heidtmann
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
