Kroppsutvidgningar II

Referenser

[F] Edition 7: Del VI: avsnitt 32, 33.

1. Kontrollfrågor om brev 9

Innan du börjar med Del VI blir det bra att kontrollera att du kan allt du läst i Del VI, avsnitt 29-31. Kontrollera även att du har inte glömt några satser och definitioner från Del I - V.

1.

Vad är en delkropp? En kroppsutvidgning?

2.

Vad säger Kroneckers sats?

3.

Vad betyder algebraisk? transcendent?

4.

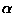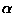Ge ett samband mellan som är transcendent över F, evalueringshomomorfien : F[x] -> E där E är en kroppsutvidgning till F.

5.

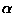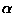Vad betyder irr(, F)? deg(, F)?

6.

Hur definieras F(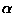)? Vad är den?

7.

Vad är en enkel utvidgning?

8.

Hur kan ett element i en enkel utvidgning skrivas?

9.

Vad är ett vektorrum?

10.

Definiera linjär beroende, linjär oberoende, bas, span.

11.

Ge en bas till F().

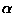12.

Vad betyder ändlig dimension?

13.

Vad är dimensionen till F()?

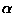14.

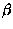
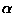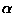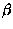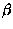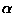Om F() och är algebraiska över F, vad kan du säga om ? Vilka är samband mellan deg(, F) och deg(, F)?

15.

Vad är en algebraisk utvidgning?

16.

Vad är en ändlig utvidgning

17.

Vad betyder [E:F]?

18.

Om [E:F]=1, vilka är samband mellan E och F?

19.

Låt K respektive E vara kropputvidgningar till E respektive F. Vilka är samband mellan deras grader över varandra?

20.

Vilka är samband mellan algebraiska utvidgningar, ändliga utvidgningar och vektorrum?

21.

Vad betyder algebraisk slutning av en kropp?

22.

Om en kropp F är algebraisk sluten, vad kan du säga om nollställen till en polynom i F[x]?

2. Läsanvisningar till Del VI i [F]

29 Introduction to Extension Fields (Brev 9)
30 Vector Spaces (Brev 9)
31 Algebraic Extensions (Brev 9)
32 Geometric Constructions
33 Finite Fields

I denna del hittar vi svaret till frågan: Låt F vara en kropp. Finns det en kropp E så att F är en delring till E och ett element a i E så att f(a)=0? E är en s.k. kroppsutvidgning av F.

Vi arbetar med begreppet kroppsutvidgning och vektorrum för att definiera en Galois kropp (avsnitt 33). Innan detta bestämmer vi vilka geometriska figurer som kan ritas med hjälp av endast passare och linjal (avsnitt 32).

32 Constructible Numbers

Detta avsnitta handlar om vilka längder och vinklar man kan rita med hjälp av endast en passare och linjal. Du bör kunna innehållet i Theorem 32.1-32.11.

Kontrollfråga 32A

1. Hur hittar man, med hjälp av endast en passare och linjal, en linjes medelpunkt?
2. Hur ritar man en linje som är parallell till en linje l genom en punkt P?
3. Varför kan man inte rita allting med hjälp av endast passare och linjal?

Övningar på avsnitt 32

Gör några övningar på avsnitt 32. För förslag, se nedan.

33 Finite Fields

KONTROLLFRGA 33A

För vilka ordningar existerar det en kropp?

Varje ändlig kropp har karakteristik p då p är ett primtal. (Varje kropp är ett integritetsområde och varje integritetsområde har karakteristik 0 eller p. (Övning 19.29) Kan en ändlig kropp ha karakteristik 0?

En kropp som har karakterisk p innehåller pⁿ element för något heltal n. (Corollary 33.2 till sats 33.1) Det betyder att det kan existera endast kroppar som har ordning pⁿ. Theorem 33.12 säger att två kroppar av ordning pⁿ är isomorfa. Sats 33.10 säger att det existerar en kropp GF(pⁿ) för varje primtal p och positivt heltal n. Observera att den multiplikativa gruppen av en ändlig kropp är cyklisk.

Övningar på avsnitt 33

Gör några övningar på avsnitt 33. För förslag, se nedan.

3. Övningar Del IX

Jag föreslår att du försöker göra alla övningar markerad med * först. Kontakta mig om du går bet på någon övning.

Avsnitt	Problem
32	3, 4
33	1, 2, 8, 9

4. Inlämningsuppgift (tisdag v. 51)

Construct a finite field with 9 elements and give its addition and multiplication tables.

5. Kontrollfrågor om brev 10

1.

Vad betyder begreppet "constructible" tal?

2.

Vilka tal är constructible?

3.

Om 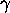är "constructible", vad är [ () : ]?

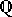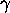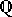4.

Ge några exempel på strukturer som är omöjliga att konstruera.

5.

Hur många element har en ändlig utvidgning E av en kropp F?

6.

Hur många element har en ändlig kropp?

7.

Vilka element innehåller den algebraiska slutningen av _p

8.

Vilka samband är det mellan ändliga utvidgningar och enkla utvidningar?

9.

För vilka x existerar GF(x)? Beskriv GF(x).