Homomorfier och faktorgrupper
Referenser
[F] Edition 7: Del III: avsnitt 13, 14, 15.
1. Kontrollfrågor om brev 3
Innan du börjar med Del III blir det bra att kontrollera att du kan allt du läst i Del II. Kontrollera även att du har inte glömt några satser och definitioner från Del I. Glöm inte att uppdatera din lista av grupper.1. Vad är en permutation?
2. Vad är Sn?
3. Hur många element finns i Sn?
4. Vad är D3? D4?
5. Vad är en bana?
6. Hur kan man skriva en permutation?
7. Hur många jämna/udda permutationer existerar?
8. Vad är en transposition?
9. Vad är A4?
10. Vad är en sidoklass?
11. Vad är Lagranges sats och vilket resultat hänvisar det till?
12. Hur bevisar man Lagranges sats?
13. När är Zm x Zn och Zmn isomorfa?
14. Vad är ordning av (a, b, c) i Zm x Zn x Zl?
15. Vad är en ekvivalensrelation? En partition?
16. Vad säger Cayleys sats? Hur bevisar man den?
2. Läsanvisningar till Del III i [F]
13 Homomorphisms Struture Relating Maps
14 Factor Groups
15 Factor-Group Computations and Simple Groups
16 - 17 Ingår ej i kursen
Isomorfier är en typ av speciella funktioner som kallas
för homomorfier. Homomorfier presenteras i denna
del. Du har sett exempel på homorfier förut t.ex.
linjära avbildningar på vektorrum.
I Del III, lär vi oss mer om sidoklasser som
tillsammans med homomorfier hjälper oss att konstruera
nya grupper, som kallas för faktorgrupper. Det är
viktigt att repetera sidoklasser ordentligt.
Avsnitt 13
Structure-Relating Maps
Kom du ihåg följande definition?En avbildning T : Rn -> Rm är linjär om
(i) T(u+v)=T(u)+T(v) för alla u,v
 Rn,
Rn,
(ii) T(kv)=kT(v) för alla u,v
 Rn och reella tal k.
Rn och reella tal k.
Tänka 13A
Del (i) är ganska likt definition 13.1. Det betyder att varje linjär avbildning är en homomorfi men är varje homomorfi från Rn till Rm en linjär avbildning, dvs har (ii) något betydelse? Det gäller att t ex T(2v)=T(v+v)=T(v)+T(v)=2T(v) och så vidare så varför har vi både villkoren? Existerar det ett exempel på en homomorfi från Rn till Rm som inte är en linjär avbildning?Sida 125: Läs genom definition 13.1, och prova följande exempel:
Kontrollfråga 13B
Låt  : <G1, *1>
: <G1, *1>
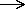 <G2, *2 >
vara en homomorfi. Skriv, med hjälp av denna notation,
ner definitionen av homomorfi.
<G2, *2 >
vara en homomorfi. Skriv, med hjälp av denna notation,
ner definitionen av homomorfi.
Vi ser i exempel 13.2 att en av struktur som konserveras av homorfier är den abelska strukturen.
Tänka 13C
-
Vilka strukturer hos en grupp tror du konserveras av en homomorfi,
dvs, låt :G
:G 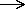 G' vara en homomorf. Vilka
egenskaper har både G och G'? Skriv
ner en lista.
G' vara en homomorf. Vilka
egenskaper har både G och G'? Skriv
ner en lista.
-
Om
 är en homomorfi från G
till G', vad kan du säga om
är en homomorfi från G
till G', vad kan du säga om  (e), där e är
G:s identitetselement, och
(e), där e är
G:s identitetselement, och  (a-1)?
(a-1)?
Tänka 13D
I exempel 13.2, ser vi att om  är en homomorfi från G till
G', och G är abelsk så är
G' öckså det, men är G abelsk om
G' är det?
är en homomorfi från G till
G', och G är abelsk så är
G' öckså det, men är G abelsk om
G' är det?
Tänka 13E
I exempel 13.3 får vi en homomorfi från Sn till Z2. Betrakta mängderna An och Bn av element som avbildas på 0 resp. 1. Observera att de är sidoklasser till Sn. Jämför följande tabell med Z2. Vilken mängd, An eller Bn, fungerar som identitetselement?
| Ê | (1)(2)(3) | (123) | (132) | (12)(3) | (13)(2) | (1)(23) |
| (1)(2)(3) | (1)(2)(3) | (123) | (132) | (12)(3) | (13)(2) | (1)(23) |
| (123) | (123) | (132) | (1)(2)(3) | (13)(2) | (1)(23) | (12)(3) |
| (132) | (132) | (1)(2)(3) | (123) | (1)(23) | (12)(3) | (13)(2) |
| (12)(3) | (12)(3) | (1)(23) | (13)(2) | (1)(2)(3) | (132) | (123) |
| (13)(2) | (13)(2) | (12)(3) | (1)(23) | (123) | (1)(2)(3) | (132) |
| (1)(23) | (1)(23) | (13)(2) | (12)(3) | (132) | (123) | (1)(2)(3) |
Tabellen ger inte gruppen Z2 men en
grupp som är isomorf med den. Denna grupp kallas
för faktorgruppen av Sn modulo
An och betecknas
Sn/An. (OBS! A/B betecknar en
faktorgrupp om A är en grupp och B är en
sidoklass till A men A\B betyder mängden A utan
element i A  B.)
B.)
Exempel 13.4 är mycket viktigt. Varför? (Se nedanstående övning)
Övning 13F
Visa att mängden A av alla polynom som har
heltalskoefficienter är en grupp under addition.
Vad är identitetselement? Är det x-3?
Nej? OK, så blir det inte bra om vi skriver
x-3=0.
Istället för rötter till en ekvation pratar
vi om nollställen till ett polynom. Om vi vill veta
vad nollställena är, så använder vi
evalueringshomomorfien: för vilka/et a
gäller  a(x-3) = 0? I detta fall är det
naturligvis a=3. Vi studerar polynom i detalj i del VI.
a(x-3) = 0? I detta fall är det
naturligvis a=3. Vi studerar polynom i detalj i del VI.
Properties of Homomorphisms
Kontrollera att du förstår definition 13.11.Kontrollfråga 13G
Låt vara en avbildning av R till R
(R=mängden av reella tal) definieras av
vara en avbildning av R till R
(R=mängden av reella tal) definieras av  (n)=n².
(n)=n².
(i) Bestäm
 [{1,2,3}].
[{1,2,3}].
(ii) Bestäm
 [R].
[R].
(iii) Bestäm
 -1[
-1[ [{1,2,3}]].
[{1,2,3}]].
Nu kan du kontrollera några av dina svar på Tänka 13C. Vi ser från sats 13.12 att identitetselement avbildas till identitetselement, inverselement avbildas på inverselement, och delgrupper avbildas på delgrupper.
Ett viktig begrepp är kärnan. I linjär algebra har du lärt dig att kärnan av en matris A är mängden av alla x sådana att Ax=0. Vad betyder det? Om vi betraktar A som en linjär avbildning är kärnan mängden av element som avbildas på 0. Det är precis samma sak här, kärnan av en homomorfi
 :G -> G' är mängden av alla
element som avbildas på e'.
:G -> G' är mängden av alla
element som avbildas på e'.
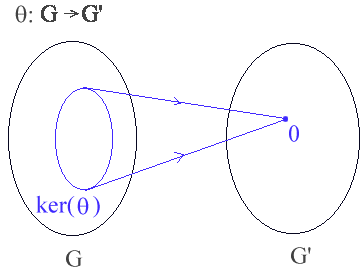
På vilket element avbildas b där b
 aKer(
aKer( )? Eftersom b
)? Eftersom b  aKer(
aKer( ) kan b skrivas som ah för
något element h
) kan b skrivas som ah för
något element h  Ker(
Ker( ). Nu gäller
). Nu gäller
 (b) (b)
|
= |
 (ah) (ah)
|
||
| Ê | = |
 (a) (a) (h) (h)
|
Ê |
 är en homomorfi är en homomorfi
|
| Ê | = |
 (a)e' (a)e'
|
Ê |
h  Ker( Ker( ) )
|
| Ê | = |
 (a) (a)
|
Ê | definition av identitetselement |
Detta betyder att varje element i aKer(
 ) avbildas på
) avbildas på  (a). (Se Figur 13.14, s130)
(a). (Se Figur 13.14, s130)
13.15 Theorem
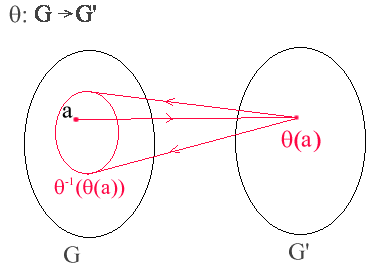
Observera att kärnan av en homomorfi är en delgrupp där vänster och höger sidoklasser är lika, dvs om H = Ker(
 ) så gäller aH = Ha.
Det betyder att kärnan är en sk normal delgrupp (se
definition 13.19, s132). Vi kommer att se att varje normal
delgrupp är kärnan till någon homomorfi.
Varför bryr vi oss om normala delgrupper? I
kontrollfråga 8C (brev 3), och avsnitt 10 såg
vi att det inte alltid är så att vänster och
höger sidoklasserna är lika. När de är
lika kan man skapa en ny grupp genom att ta sidoklasserna som
element. Så, om vi har en normal delgrupp, har vi
möjlighet att skapa en ny grupp. Vi bestämmer
ekvivalenta villkor till villkoren i definitionen av normal
delgrupp (s. 132) i avsnitt 14 (s. 141).
) så gäller aH = Ha.
Det betyder att kärnan är en sk normal delgrupp (se
definition 13.19, s132). Vi kommer att se att varje normal
delgrupp är kärnan till någon homomorfi.
Varför bryr vi oss om normala delgrupper? I
kontrollfråga 8C (brev 3), och avsnitt 10 såg
vi att det inte alltid är så att vänster och
höger sidoklasserna är lika. När de är
lika kan man skapa en ny grupp genom att ta sidoklasserna som
element. Så, om vi har en normal delgrupp, har vi
möjlighet att skapa en ny grupp. Vi bestämmer
ekvivalenta villkor till villkoren i definitionen av normal
delgrupp (s. 132) i avsnitt 14 (s. 141).
Övning 13H
13.52 sida 13513.18 Corollary
Jmf Corollary 13.18 med linjära avbildningar. I avsnitt 3 hade vi ett sätt att kontrollera om en funktion är en isomorfi. Nu har vi ett annat sätt.| Avsnitt 3 | Avsnitt 13 |
 (xy) = (xy) =  (x) (x) (y) (y)
|
 är en homomorfi är en homomorfi
|
 är en injektion är en injektion
|
Ker( ) = {e} ) = {e}
|
 är en surjektion är en surjektion
|
 är en surjektion är en surjektion
|
Övningar på avsnitt 13
Gör några övningar på avsnitt 13. För förslag, se nedan.Avsnitt 14
Factor Groups from homomorphisms
I Tänka 13E fick vi en grupp genom att dela Sn i sidoklasser, och betrakta sidoklasserna som element i den nya gruppen. Detta avsnitt handlar om när sidoklasserna ger en sk faktorgrupp och deras relation med homomorfier. Vi ser att varje normal delgrupp är kärnan till en homomorfi och ger en faktorgrupp.Gör följande övning för att hjälpa dig att förstå sats 14.1.
Kontrollfråga 14A
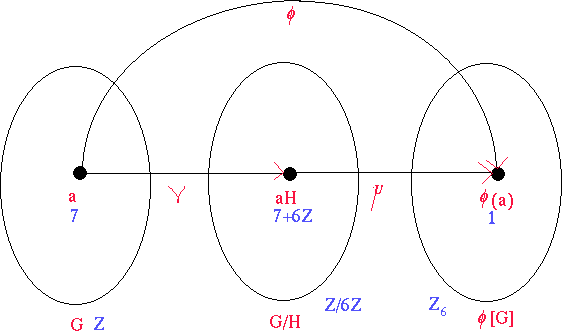
Betrakta
 : Z -> Z6 där
: Z -> Z6 där
 (a) = resten när a divideras
med 6, 0
(a) = resten när a divideras
med 6, 0  a < 6.
a < 6.
1. Bestäm H = Ker(
 ).
).
2. Vad är de vänstra och högra sidoklasserna till H? Är de lika?
3. Hur adderar man två sidoklasser?
4. Bestäm faktorgruppen Z/H som i sats 3.2.1. Vad är elementen i faktorgruppen?
5. Bestäm avbildningen
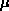 : Z/H -> Z6
så att
: Z/H -> Z6
så att 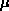 är en isomorfi.
är en isomorfi.
Factor Groups from Normal Subgroups
Nu har vi sett att man kan konstruera en faktorgrupp med hjälp av en homomorfi, men homomorfin behövs inte! För att få en faktorgrupp måste sidoklassmultiplikation vara väl definierad, och det händer när vänster och höger sidoklasser är lika (se sats 14.4). Corollary 14.5 visar att om vänster och höger sidoklasser av en delgrupp H är lika, då kan man konstruera en faktorgrupp. Det betyder att H är en normal delgrupp.14.4 Theorem
Detta sats visar att vi inte behöver en homomorfi för att bestämma produkten av sidoklasser. Kontrollera varje steg i beviset. De vänstra och högra sidoklasserna är lika. Varför måste man använda h3 och inte bara skriva a(h1b)h2 = a(bh1)h2?Fundamental Homomorphism Theorem
Fundamentala homomorfisatsen är mycket viktig inom
abstrakt algebra. Du ska kunna den och dess bevis. Vad
säger det? Att alla möjliga homomorfier  från en grupp ges precis av de olika
möjliga faktorgrupperna G/H där H
är en normal delgrupp till G och Ker(
från en grupp ges precis av de olika
möjliga faktorgrupperna G/H där H
är en normal delgrupp till G och Ker( ).
).
Kontrollfråga 14B
Titta på exempel 14.12.Lista elementen i Z4 × Z2.
Lista sidoklasserna till {0} × Z2.
Bestäm en homomorfi från Z4 × Z2 till (Z4 × Z2) / ({0} × Z2).
Bestäm en isomorfi från (Z4 × Z2) / ({0} × Z2) till Z4.
Kontrollfråga 14C
Hur ser ett element i en faktorgrupp ut?14.21, 14.22
Normal Subgroups and Inner Automorphisms
Kontrollera att du förstår varför de tre villkoren på sida 141 är ekvivalent med definition av en normal delgrupp.Övningar på avsnitt 14
Gör några övningar på avsnitt 14. För förslag, se nedan.Avsnitt 15 (ej delavsnittet om Simple Groups s. 148 - 151)
Mer exempel på faktorgrupper. Det är nyttigt att arbeta genom dem, speciellt exempel 15.6, och sats 15.9.3. Övningar Del III
Jag föreslår att du försoker göra alla övningar markerad med * först. Kontakta mig om du går bet på någon övning.| Avsnitt | Problem |
| 13 | 1*, 3, 5, 17*, 19, 25, 26, 27, 32, 51*, 52 |
| 14 | 1*, 2, 3, 4, 5, 9*, 11, 21, 22, 23, 24* |
4. Inlämningsuppgift (tisdag v. 41)
[F] Avsnitt 13: Övning 51;
[F] Avsnitt 14: Övning 24.
This is the 2nd Edition of Letter 4 for Abstract Algebra,
written by Sarah Norell in 1999 and revised in 2007 by Pia Heidtmann.
The letter may be printed for personal use by
anybody with an interest.
This letter and any parts of it and any previous and future versions of it must not
be copied or disseminated in any printed or electronic form
or stored on any publicly accessible website other than
http://www.tfm.miun.se/~piahei/algc/letters/
without permission from the author.
The author welcomes comments and corrections via email.
All contributions incorporated in updates of the manuscript will be acknowledged.
The author would like to thank the following for their contribution
to various updates of the original manuscript:
Pia Heidtmann.
c/o Pia Heidtmann
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
