Ringar och Kroppar A
Referenser
[F] Edition 7: Del IV: avsnitt 18, 19, 20, 21.
1. Kontrollfrågor om brev 4
Innan du börjar med Del III blir det bra att kontrollera att du kan allt du läst i Del III. Kontrollera även att du har inte glömt några satser och definitioner från Del I och Del II.- Vad betyder "homomorf"?
- Ge ett exempel på en homomorfi.
- Vad betyder "kärna"? Ge ett exempel.
- Vad är en delgrupp?
- Vad är en normal delgrupp?
- Ge ett exempel på en normal delgrupp.
- Vad är en isomorfi?
- Hur visar man att två grupper är isomorfa? Ej isomorfa?
- Vad säger Cayleys sats?
- Vad är en faktorgrupp?
- Ge ett exempel på en faktorgrupp.
- Hur definieras sidoklass-multiplikationen?
- Vad är en automorfi?
- Vad är den inre automorfin?
- Vad säger den fundamentala homomorfisatsen? Vad betyder det?
- Hur visar man att An inte har en delmängd av ordning 6?
2. Läsanvisningar till Del IV i [F]
18 Rings and Fields
19 Integral Domains
20 Fermat's and Euler's Theorems
21 The Field of Quotients of an Integral Domain
22 Rings of Polynomials (se brev 6)
23 Factorization of Polynomials over a Field (se brev 6)
24 Noncommutative Examples, Quaternions s 224-226 (se brev 6)
Vi började kursen med att studera strukturen hos en mängd G
som är sluten under en binär operation *. Om * är associativ,
det existerar ett identitetselement i G, och varje element i
G har en invers i G, då är <G, *> en grupp. Om
* också är kommutativ så är <G, *> en abelsk grupp.
Nu börjar vi med en abelsk grupp <G, +>, och
introducerar en annan binär operation " " på G.
Om
" på G.
Om  är associativ,
a
är associativ,
a (b + c)=a
(b + c)=a b +
a
b +
a c och
(a + b)
c och
(a + b) c=a
c=a c +
b
c +
b c
så är
<G, +,
c
så är
<G, +,  > en ring. Om
> en ring. Om
 också är kommutativ då är <G, +,
också är kommutativ då är <G, +,  >
en kommutativ ring, och så vidare.
>
en kommutativ ring, och så vidare.
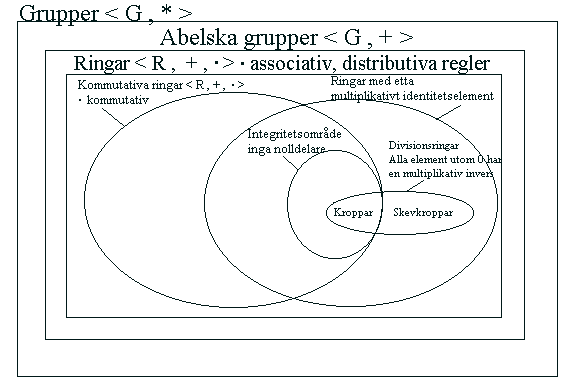
Denna del handlar om ringar, kroppar (engelska: fields) och
integritetsområden (engelska: integral domains). Många begrepp och
resultat från del I-III generaliseras - jmf satserna och definitioner
med dem i del I-III.
Vi börjar att studera polynom nästa vecka i avsnitt 22.
18 Rings and Fields
Detta avsnitt börjar med definitionen av en ring (definition 18.1).
Tänka 18A
Låt < R, +,  > vara en ring.
Från definitionen, vet vi att < R, +> är en abelsk grupp.
> vara en ring.
Från definitionen, vet vi att < R, +> är en abelsk grupp.
När är
< R*, > en grupp?
> en grupp?
Tänka 18B
Varför står det "left distributive law and right distributive law hold" istället för bara "distributive law"?
Kontrollfråga 18C
Skriv ner multiplikationstabell och additionstabell för
 4.
4.
Kontrollfråga 18D
Vilka av följande är ringer (med de vanliga additionen och
multiplikationen)?
För de som är ringer:
(a) vilka har ett multiplikativt identitetselement (etta)?
(b) i vilka existerar det en multiplikativ invers till alla element utom 0?
(c) i vilka är multiplikation kommutativ?
 |
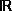 |
2 |
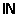 |
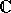 |
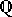 |
M2 (mängden av invertibara 2 × 2 reella matriser) |
Theorem 18.8
Är det självklart hur man bevisar alla delar i denna sats? Försök att skriva ner ett överblick över hur bevisen går till. Finns det några specialknep som du kanske kan använda i ett annat bevis?Homomorphisms and Isomorphisms
Observera att en ringhomomorfi : R -> R'
är också en grupphomomorfi
: R -> R'
är också en grupphomomorfi  : < R, + > ->
< R',+'>.
: < R, + > ->
< R',+'>.Kontrollfråga 18E
Som sagt i brev 4, är evaluationshomomorfien viktig. Läs genom Example 18.10 och gör Exercise 35 sidan 176.Multiplicative Questions; Fields
Efter definitionen av kommutativ ring och etta (engelska: unity) (definition 18.14) är en viktig kommentar: (n.1)(m.1) = (mn).1 som illustreras av Example 18.15.På s 173 får vi svaret till frågan: när är < R*,
 >
en grupp? Om < R*,
>
en grupp? Om < R*,  >, då innehåller R
en etta (multiplikativt identitetselement) och varje icke-noll element
i R är en enhet (dvs, har en multiplikativ invers). En sådanna ring
kallas för en divisionsring, och om < R*,
>, då innehåller R
en etta (multiplikativt identitetselement) och varje icke-noll element
i R är en enhet (dvs, har en multiplikativ invers). En sådanna ring
kallas för en divisionsring, och om < R*,  >
är abelsk, kallas det för en kropp. Om det inte är kommutativt, kallas
det för en skevkropp.
>
är abelsk, kallas det för en kropp. Om det inte är kommutativt, kallas
det för en skevkropp.
Viktig övningpå avsnitt 18
18.37 (inlämningsuppgift)Kontrollera att du kan alla definitioner!
Övningar på avsnitt 18
Gör några övningar på avsnitt 18. För förslag, se nedan.19 Integral Domains
Betrakta ekvationen ab = ac där a, b, c tillhör S. Om S är en grupp gäller b = c. Om S =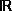 gäller a = 0 eller b = c.
Om S =
gäller a = 0 eller b = c.
Om S =  8, då
finns det också andra lösningar, t ex a = 2 och b - c = 4.
Varför? För att
8, då
finns det också andra lösningar, t ex a = 2 och b - c = 4.
Varför? För att  8
har nolldelare, dvs det existerar nollskilda element a och
b i
8
har nolldelare, dvs det existerar nollskilda element a och
b i
 8 så att ab = 0.
8 så att ab = 0. Vilka element i
 n är nolldelare?
Theorem 19.3 och Corollary 19.4 visa att alla element som
inte är relativa prima med n är nolldelare. Det betyder att
om n är ett primtal så har
n är nolldelare?
Theorem 19.3 och Corollary 19.4 visa att alla element som
inte är relativa prima med n är nolldelare. Det betyder att
om n är ett primtal så har  n
ingen nolldelare.
n
ingen nolldelare.
Kontrollfråga 19A
Hur många nolldelare finns det i n?
n?
Tänka 19B
Om p är ett primtal, vad kan du säga om strukturen av p? Är det en divisionsring?
en kropp? en skevring?
p? Är det en divisionsring?
en kropp? en skevring?ISBN - ej i boken
Att n saknar nolldelare då n
är ett primtal har viktiga praktiska tillämpningar. Hur fungerar ISBN?
Det bygger på det faktum att
n saknar nolldelare då n
är ett primtal har viktiga praktiska tillämpningar. Hur fungerar ISBN?
Det bygger på det faktum att
 11 saknar nolldelare.
A First Course in Abstract Algebra 5e: upplag har ISBN 0-201-59291-6.
11 saknar nolldelare.
A First Course in Abstract Algebra 5e: upplag har ISBN 0-201-59291-6.
| 0 | 201 | 59291 | 6 |
| språk | bokförlag | bokförlagets eget boknummer | checksiffra |
Hur beräknar man checksiffran? Låt (a1a2a3a4a5a6a7a8a9a10) vara ett ISBN.
Då är 1a1 + 2a2 + 3a3 + 4a4 + 5a5+ 6a6 + 7a7 + 8a8 + 9a9+ 10a10
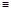 0 (mod 11).
Vad kontrollerar checksiffran? Om en siffra är fel eller två siffror har
bytt plats blir inte summan ovan lika med 0 (mod 11), då vet man
att det finns minst ett fel, men tyvärr inte precis vad felet är.
0 (mod 11).
Vad kontrollerar checksiffran? Om en siffra är fel eller två siffror har
bytt plats blir inte summan ovan lika med 0 (mod 11), då vet man
att det finns minst ett fel, men tyvärr inte precis vad felet är.
Integral Domains
Ett integritetsområde är en divisionsring som inte har nolldelare. Vad är sambandet mellan integritetsområden och kroppar? Svaret hittar du i Theorem 19.9 och Theorem 19.11. Lär dig dessa två satserna med bevis. Observera metoden i beviset av 19.11. Den kommer du att använda igen i avsnitt 20.Kontrollfråga 19C
Vad är relationen mellan integritetsområden, kroppar, divisionsringar och skevkroppar?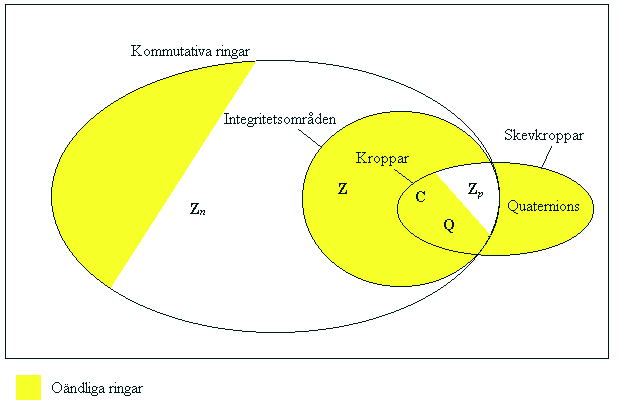
Kontrollfråga 19D
Ge ett exempel på(i) en ändlig integritetsområde som inte är en kropp,
(ii) en oändlig integritetsområde som inte är en kropp,
(iii) en ändlig kropp som inte är en integritetsområde,
(iv) en oändlig kropp som inte är en integritetsområde.
The Characteristic of a Ring
Kontrollera att du förstår begreppet karakteristik av en ring och Theorem 19.15.Kontrollfråga 19E
Låt R vara en kommutativ ring med etta. Anta att R har karakteristik 3. Förenkla (a² + b)² där a, b R.
R.Kontrollfråga 19F
Gör övning 19.29Övningar på avsnitt 19
Gör några övningar på avsnitt 19. För förslag, se nedan.20 Fermat's and Euler's Theorems
Lär dig sats 20.1 och 20.8 med bevis.Fermat's Little Theorem
Om a
 och p är ett
primtal så att p inte är en delare till a, då är p
en delare till ap-1 - 1, dvs ap-1
och p är ett
primtal så att p inte är en delare till a, då är p
en delare till ap-1 - 1, dvs ap-1
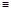 1 (mod p) för a
1 (mod p) för a
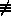 0 (mod p).
0 (mod p).
Bevis

|
Visa att
ringen  n är isomorf med n är isomorf med
 /n /n .
Observera att
sidoklass multiplikation definieras av
(a+n .
Observera att
sidoklass multiplikation definieras av
(a+n )(b+n )(b+n ) = ab +
n ) = ab +
n är väldefinierad. är väldefinierad.
|

|
Det existerar b  där där  ,
1 ,
1  b b  p-1 och
a p-1 och
a 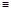 b
(mod p). b
(mod p).
|

|
För varje kropp, mängden av icke-noll element ger en grupp
under kroppsmultiplikation. (Se övning 18.37 (sidan 176))
Det betyder att element 1,2,3,...,p-1 i
 p ger en grupp under multiplikation
modulo
p. Gruppen har ordning p-1 och varje elements ordning t
delar ordning av gruppen, dvs tu=p-1 för något heltal u.
Vad betyder ordning t av ett element b?
Det betyder att t är det minsta positiva heltal så att
bt=1. Nu, bp-1 = btu =
1u = 1 i p ger en grupp under multiplikation
modulo
p. Gruppen har ordning p-1 och varje elements ordning t
delar ordning av gruppen, dvs tu=p-1 för något heltal u.
Vad betyder ordning t av ett element b?
Det betyder att t är det minsta positiva heltal så att
bt=1. Nu, bp-1 = btu =
1u = 1 i  p, dvs
ap-1 p, dvs
ap-1
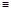 1 (mod p) för a 1 (mod p) för a
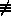 0 (mod p). 0 (mod p).
|
Kontrollfråga 20A
Skriv ner ett överblick av beviset av Theorem 20.6 och Eulers sats 20.8.Application to ax 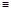 b (mod m)
b (mod m)
Jämför detta avsnitt med resultat från andra kurser, t ex
lösningar till diofantiska ekvationer och ekvationer modulo n i Algebra och Diskret Matematik.
Övningar på avsnitt 20
Gör några övningar på avsnitt 20. För förslag, se nedan.21 The Field of Quotients of an Integral Domain
Läs genom avsnittet men du behöver inte bry dig för mycket om detaljerna.
3. Övningar Del IV.A
Jag föreslår att du försoker göra alla övningar markerad med * först. Kontakta mig om du går bet på någon övning.| Avsnitt | Problem |
| 18 | 7, 10, 11, 14*, 15*, 16*, 22, 23, 27, 33, 35, 37*; |
| 19 | 5, 7, 9, 13, 17, 23, 29*; |
| 20 | 6, 10, 14, 23. |
4. Inlämningsuppgift (tisdag v. 42)
[F] Avsnitt 18: Övning 37.
This is the 2nd Edition of Letter 5 for Abstract Algebra,
written by Sarah Norell in 1999 and revised in 2007 by Pia Heidtmann.
The letter may be printed for personal use by
anybody with an interest.
This letter and any parts of it and any previous and future versions of it must not
be copied or disseminated in any printed or electronic form
or stored on any publicly accessible website other than
http://www.tfm.miun.se/~piahei/algc/letters/
without permission from the author.
The author welcomes comments and corrections via email.
All contributions incorporated in updates of the manuscript will be acknowledged.
The author would like to thank the following for their contribution
to various updates of the original manuscript:
Pia Heidtmann.
c/o Pia Heidtmann
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
