
Latin Squares

Latin squares are very useful in the design of experiments. Take the following example. A company research department is delevoping some new fertilizers. These need to be tested to see which is the most effective. The company has a field available for testing. (See Figure 1.) At the northern edge of the field is a row of trees and to the south is a river. There are often easterly winds blowing across the field. These factors make it impossible to simply split the field into strips since the ones near the river may be wetter, and the ones near the trees have a more nutritional soil due to decayed leaves, or maybe the shade from the trees will make a difference. Another problem is the wind, if the strips are taken the other way. The crops to the east may be more protected than those to the west. So to eliminate some of the influence of these factors, the company decides to divide the field into a grid. It wants the fertilizers to be placed so that each fertilizer occurs exactly once in each row and exactly once in each column. Can this be done and, if so, how?
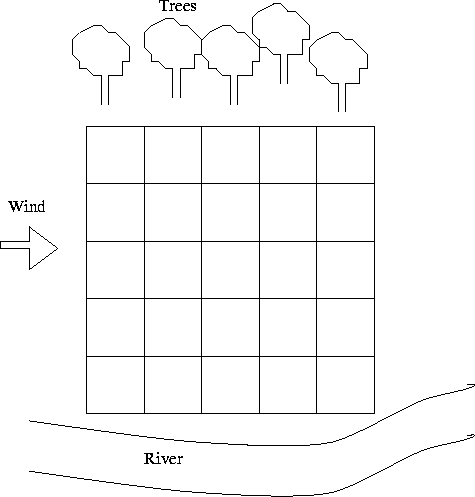
Figure 1: Example of the Problem with Five Fertilizers.
This problem can be quite simply solved by using modular arithmetic. First we define a latin square and then we will show one method for constructing an n × n latin square.
Definition
A latin square of order n is an n × n
array in which each of n
symbols occurs exactly once in each row and column.
We label the rows and columns of an n × n
latin square with the
elements of 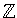 n.
n.
[ By 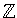 n we mean the
integers 0, 1, 2, ..., n-1 with all arithmetic conducted
modulo n.]
n we mean the
integers 0, 1, 2, ..., n-1 with all arithmetic conducted
modulo n.]
The elements in the latin square will also be the elements of
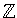 n.
We use the notation L(i,j) to mean the entry in the ith row and jth column.
n.
We use the notation L(i,j) to mean the entry in the ith row and jth column.
Theorem
The array defined by
L(i,j)=i+j, where i and j are elements of
 n.
is a latin square.
n.
is a latin square.
Proof
To show that this is true we need to show that no two entries in the same row are the same. A similar argument will show that there are no two entries which are the same in any column.
We use proof by contradiction. Suppose that
L(i,j)=L(i,j'), j  j'.
Then i+j=i+j'. Subtracting i from both sides, we see that j=j' and
we have a contradiction. Hence no element occur twice in the same
row. Since there are only n elements, each element must occur exactly
one in each row.
A similar argument proves that each element occurs exactly once
in each column. Q.E.D
j'.
Then i+j=i+j'. Subtracting i from both sides, we see that j=j' and
we have a contradiction. Hence no element occur twice in the same
row. Since there are only n elements, each element must occur exactly
one in each row.
A similar argument proves that each element occurs exactly once
in each column. Q.E.D
So given any n, we can create a latin square of that order. If we have a partially constructed latin square - that is a few rows which satisfy the condition that each element occurs exactly once in each row, and no column contains the same element twice - can we extend this to form a latin square? This rectangular array is called a latin rectangle.
A latin rectangle can always be extended to form a latin square. (See figure 2.) We will not prove this result. (The proof can be found in Combinatorics: Topics, Techniques, Algorithms - Peter J. Cameron, Cambridge University Press, chapter 6.)
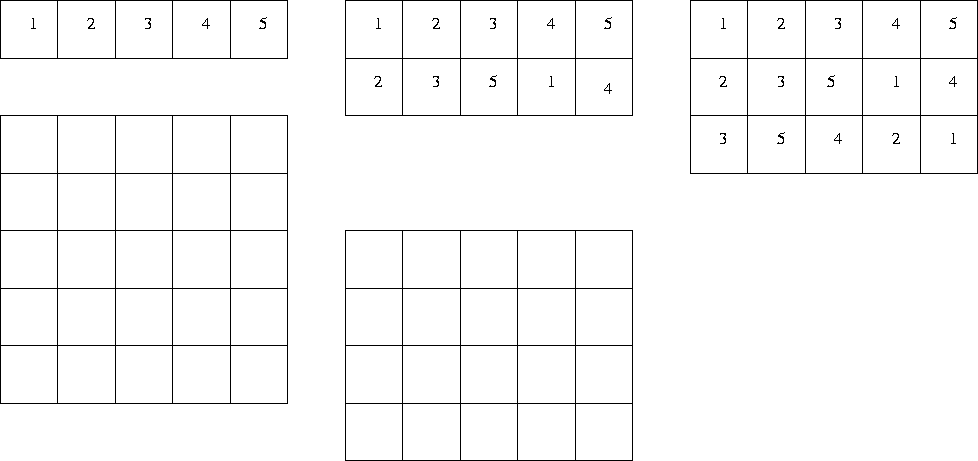
Figure 2: A latin rectangle extended to a latin square
Another situation where latin squares are useful is given in the following problem.
A University is made up of five colleges. It has been experiencing difficulties with communication between the five colleges and the five different departments within the individual colleges. It has been decided that the five main committees which run the University will consist of one representative from each college and each department. Now, due to internal politics, if one college or department has two chairmen, the other colleges and departments will feel that this is unjust. This is also the case for the positions of secretary, treasurer, public relations officer and spokesman. So if each college sends one person from each of the five departments, is it possible to make up the committees so that everyone is happy, at least until they start their discussions?
This problem is related to a famous problem about thirty six officers posed by Euler in 1781. The problem is as follows. Suppose there are thirty six officers from six different regiments and of six different ranks, where no two officers of the same rank are from the same regiment. Can they be arranged in a 6 × 6 block so that no two officers of the same rank or from the same regiment are in the same row or column?
Euler knew that there was a solution for all n not congruent to 2 (mod 4).
He conjectured that there was no solution for n=6, and not only that, but also
that it is impossible if n  2
(mod 4) where n is the number of
regiments and ranks. He was partly correct. It is not possible for n=6,
but this was not proved until 1900 by Tarry.
In 1960, it was proved
by Bose, Shrikhande and Parker that there is a solution for all
n except n=2 and n=6.
2
(mod 4) where n is the number of
regiments and ranks. He was partly correct. It is not possible for n=6,
but this was not proved until 1900 by Tarry.
In 1960, it was proved
by Bose, Shrikhande and Parker that there is a solution for all
n except n=2 and n=6.
Definition
A pair of latin squares L1 and L2
of the same order are said to be orthogonal if
for every ordered pair of symbols (k,k'), there is exactly one position
(i,j) so that
L1(i,j)=k and
L2(i,j)=k'.
To solve the thirty six officers problem we would need to find two
orthogonal latin squares of order 6, and as we commented above, there
are no orthogonal latin squares of order 6.
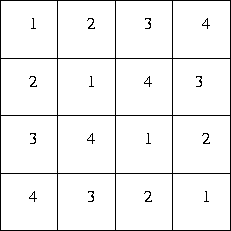
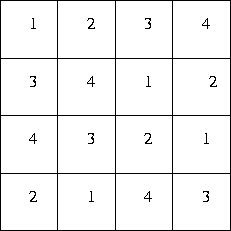
Figure 3: Two orthogonal latin squares of order 4.
We will consider first the case where n>2 is prime.
Theorem
Let p>2 be prime and t an integer 1  t < p.
Then the arrays
given by
t < p.
Then the arrays
given by

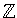 p.
p.
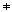 t.
t.
The proof is left as an exercise. It requires the proof that Lt is a
latin square for each t, and then that any two latin squares where u 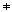 t.
t.
Defintion
A set of latin squares which are pairwise orthogonal is called a
set of mutually orthogonal latin squares or a set of MOLS.
From the above theorem we can see that for any prime p>2, there is a set of p-1 MOLS.
The following method gives latin squares for some non-prime orders. However, there is no general method know for constructing orthogonal latin squares.
Let Lt and Lu be orthogonal latin squares of order n and let Lx and Ly be orthogonal latin squares of order m. Then we can combine them to form a pair of orthogonal latin squares of order mn as follows.
Divide the mn elements of the new latin square into sets of n, and form these into m latin squares of the form of Lt. Then use these latin squares as the entries in Lx. Do the same thing for Lu and Ly. (Note that this is also a method for creating latin squares which differs from the method above.)
| 1A: |
|
2A: |
|
3A: |
|
4A: |
|
1B: |
|
2B: |
|
3B: |
|
4B: |
|
Figure 4: Building a Latin Square of Order 12 from Orthogonal Latin Squares of Order 3 and 4
In the first 4 × 4
latin square in figure 3, we replace all
the 1's in by the latin square labelled 1A, all the 2's by the
latin squares labelled 2A and so on. Do the same for the second
latin square in figure 3 and the latin squares labelled B,
that is, replace all the 1's by 1B, 2's by 2B and so on.
|
|
|
4A | |||||||||||||||||||||||||||
|
|
4A |
|
|||||||||||||||||||||||||||
| 4A |
|
| |||||||||||||||||||||||||||
| 4A |
|
|
|
|
2B | 3B | 4B | |||||||||
| 3B | 4B |
|
2B | |||||||||
| 4B | 3B | 2B |
| |||||||||
| 2B |
|
4B | 3B |
Figure 5: Partially Formed Orthogonal Latin Squares of order 12
Exercises
1. Show that there is only one latin square of order 1, 2 and 3, upto the permutation of the rows and symbols, and two of order 4. Show that one of the latin squares of order 4 has an orthogonal partner and the other does not.
2. Find four MOLS of order 5.
3. Construct a pair of orthogonal latin squares of order 15.