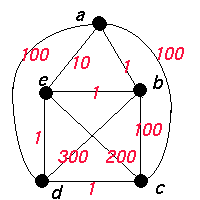
w(ab)+w(be) < w(ae)
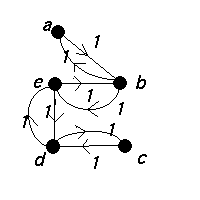
The minimum weight of a hamilton cycle is 104 (abedca). The best route is actually given by traversing each edge of the minimum spanning tree twice.

 |
This graph does not satisfy the triangle inequality (see below) as
for instance w(ab)+w(be) < w(ae) |
 |
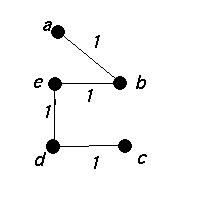
A minimum spanning tree in this graph is |

|
An upper bound for the problem is
2×(weight of a minimum spanning tree) =2 × 4 = 8. The minimum weight of a hamilton cycle is 104 (abedca). The best route is actually given by traversing each edge of the minimum spanning tree twice. |
 w(xz),
where w(ab) is the
weight of the edge ab. Then a
shortest route around all the customers is
a Hamiltonian cycle.
w(xz),
where w(ab) is the
weight of the edge ab. Then a
shortest route around all the customers is
a Hamiltonian cycle.
 |
 |
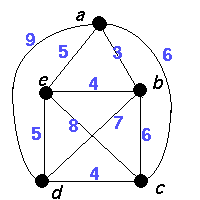 |
Start at a, add b, path ab, length 3 from b, add e, path abe, length 7 from e, add d, path abed, length 13 from d, add c, path abedc, length 17. |
| "Getting a precise answer to this optimization problem is not
easy. Currently, the world's record for the Traveling
Salesperson Problem is just over 3,000 cities. That solution
required the creative energies of four top researchers and
the dedicated use of almost one month's time on a
supercomputer.
"In sharp contrast, you can get a pretty good approximation to the optimal solution in a very short time. This is a common theme of many discrete math problems. " |
|
"If you can come within a reasonable
degree of the right answer, in a
reasonable amount of time, and at
reasonable cost, you may consider
that you've solved the problem-at
least in the real world."
HAL KIERSTEAD |
| 1 | 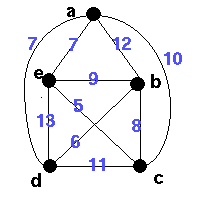 |
2 | 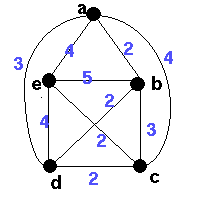 |