

Earlier, we have talked about even numbers and that we can write them as 2k where k is an integer. Here, we look into the question of divisibility and factors some more.
Let a,b be integers. Then b is a divisor (factor, delare, faktor) of a if a
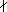 a.
a.
It is important to notice that the expression 'a är delbart med b' means that there is no remainder when 'a delas med b' - we do not need to add the word 'jämnt.'
What results do we know about divisibility? The following theorem summarizes some of them.
Let a,b,c be integers
| Proof | Comments |
|
Whenever we try to prove something involving division, we need to think about the definition. The definition says that if x is divisible by y then there exists an integer k so that yk=x. We use this and a direct proof in each case. Note that if we have for instance, a | b and b | c then we must use different letters to represent integers, say s and t, so that as=b and bt=c. |
While we are considering divisibility, we need to consider prime numbers, but what exactly is a prime number?
A positive integer p > 1 which has only the divisors 1 and itself
is called a prime number or simply a prime (primtal).
A positive integer n  2 which
is not a prime is called a composite number (sammansatt tal).
2 which
is not a prime is called a composite number (sammansatt tal).
What results do we know about primes? When we try to factorize a number
into primes, can we always do it? (We consider 5 to already be the product
of primes, although it is just the product of one prime, 5 itself!.)
In how many different ways can we do it?
If we factorize 6 we get 3 2 or
2
2 or
2 3 which are the same if we ignore
the order of the prime factors. Is this always the case? The follow
theorem says that it is.
3 which are the same if we ignore
the order of the prime factors. Is this always the case? The follow
theorem says that it is.
Every integer n  2 can be written as the
product of
primes. There is exactly one way to do this upto the order of the factors.
2 can be written as the
product of
primes. There is exactly one way to do this upto the order of the factors.
We omit the proof of this result for the moment.
How many primes are there? Is there always 'one more' to be found, or do they run out at some point? The following result says that there are infinitely many primes. This is an important proof, which you should know.
There are infinitely many primes.
| Proof (Euclid) | Comments |
Suppose there is a finite number of primes. Then we can list all of them as
p1, p2, ..., pk. Consider
n=p1p2...pk+1. Every integer greater than
1 can be written as the unique product of primes upto the order of the primes,
(Fundamental Theorem of Arithmetic) so n has prime
factors. Now n is not divisible
by pi for 1  i i
 k, so n has a prime factor q
(which may be n itself) which is not
pi for any i, 1 k, so n has a prime factor q
(which may be n itself) which is not
pi for any i, 1  i i
 k. Hence q is not in the list, so the
list is incomplete, which is a contradiction. Therefore there is an
infinite number of primes. k. Hence q is not in the list, so the
list is incomplete, which is a contradiction. Therefore there is an
infinite number of primes.
| We use contradiction here. We know that if we have a finite set, then we can make a complete (finite) list of all the elements. We will find a prime which is not in our list - which gives us a contradiction. |
Now we know that there are infinitely many primes numbers, how do we find them? Basically, we pick a number and then test it to see if it has any divisors. Do we have to test all integers from 2 upto the number we are testing? No. It is enough to test upto its square root.
Let n  2 be an integer. If there
is no prime factor k of n where 1
2 be an integer. If there
is no prime factor k of n where 1  k
k

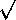 n,
then n is a prime.
n,
then n is a prime.
| Proof | Comments |
|
Suppose n |
What we are trying to prove is a bit confusing, isn't it? Maybe trying an
example to see what it means might help us to start with.
We know what a prime is. Now for an example. Let's take
n=61. Then We're going to try to prove this using contradiction so we have to decide what we are going to assume. Ok, so we assume the part between "if" and "then": n has
no factor k where 1
 k k  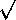 n n
and "not" the bit after the "then":
and n is not prime.
|
As p is not prime, it has postive factors a,b such that
n=ab and 1 < a |
Now we have to do something, but what? If n is not prime, what is it then?
It's an integer which has positive factors which aren't 1 or n, so we can
write n=ab for some integers a and b, and just to make
life easier, let's
take a |
Suppose a > 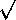 n. Then
n= ab > n. Then
n= ab > 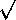 n n
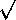 n = n, which is
a contradiction so a n = n, which is
a contradiction so a 
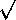 n. n.
|
What do we know about the size of a? Well, if it is bigger
than 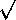 n we are in trouble
as then a and b are both big and their product ab
is the greater than n.
This means that a must be at most n we are in trouble
as then a and b are both big and their product ab
is the greater than n.
This means that a must be at most
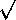 n. Ah, so we have a factor
a of n which is at most n. Ah, so we have a factor
a of n which is at most 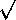 n. n.
|
By the Fundamental Theorem of Arithmetic, a has a prime factorization.
Suppose p is a prime factor of a. Then 1 < p
 a a  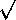 n. Now p|a and a|n so p|n, which is a contradiction as we assumed
that n has no such prime factors. This completes the proof. n. Now p|a and a|n so p|n, which is a contradiction as we assumed
that n has no such prime factors. This completes the proof.
|
Now,
if we find a prime factor of n which isn't too big,
we have a contradiction.
Hopefully, we can use a to find this factor - it could even be a!
We know that every integer greater than 1 can be expressed at the
product of primes,
so a has
a prime factor p, which is thus also a factor of n
and p is at most as big as a and
a is at most 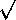 n.
This is a contradiction as we said n has no prime factor which
is at most n.
This is a contradiction as we said n has no prime factor which
is at most 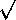 n, so our
assumption that n is not prime is false and n is prime. n, so our
assumption that n is not prime is false and n is prime.
|
Is 437 a prime?
We test all primes upto 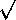 437 which
is around 22. The primes upto 22 are: 2, 3, 5, 7, 11, 13, 17, 19.
We find that 19 is a factor of 437 so it is not a prime.
437 which
is around 22. The primes upto 22 are: 2, 3, 5, 7, 11, 13, 17, 19.
We find that 19 is a factor of 437 so it is not a prime.
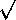 5 is irrational.
(Hint: Compare with the proof that
5 is irrational.
(Hint: Compare with the proof that 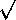 2
is irrational on page 17 in Chetwynd and Diggle.)
2
is irrational on page 17 in Chetwynd and Diggle.)