

An interesting application of modulus is in ISBN. Maybe you have wondered why some books have an ISBN which ends in X? This is because the last digit is a check digit, calculated modulo 11, so an extra 'digit' is required to symbolise 10. How is the check digit calculated? It is a weighed sum, which means that each digit is multiplied by a fixed amount, and then the sum is taken. Suppose the ISBN is a1a2a3a4a5a6a7a8a9a10. Then the weighted sum is
 6+1-3+6-1-3-6
6+1-3+6-1-3-6  0 (mod 11). The advantage of
this system is that if two digits are switched, or if one digit is incorrect,
then the weighted sum is not congruent to 0 modulo 11, so we know there is
an error somewhere although we do not know where or what it might be.
0 (mod 11). The advantage of
this system is that if two digits are switched, or if one digit is incorrect,
then the weighted sum is not congruent to 0 modulo 11, so we know there is
an error somewhere although we do not know where or what it might be.
 b (mod n)
b (mod n)Next we are going to look at solving congruences, but first, let's consider the following situtation. Suppose
 4.
4.Then we cancel and get x=4. Nothing strange about that. Now let's look at the same thing, but this time, modulo 24:
 3
3 4 (mod 24).
4 (mod 24).
Is it true to say that x 4? What
if x
4? What
if x 12? Then
12? Then
 12
12
 36
36 12
12 3
3 4 (mod 24).
4 (mod 24).This illustrates the fact that we must be very careful when cancelling while working with congruences. What you might wonder is if there is ever a time when we can cancel, and yes there is. We will come to that in a moment, after we have looked at the problem a bit more.
Solve the equations
 8 (mod 4)
8 (mod 4)
 3 (mod 4)
3 (mod 4)
 2 (mod 4)
2 (mod 4)
We use trial and error.
 0 (mod 4)
or x
0 (mod 4)
or x  2 (mod 4).
2 (mod 4).
 2 (mod 4).
2 (mod 4).
We mentioned earlier than if ax  b (mod n), then we can write ax+nq=b for some integer q. From a result
on diophantine equations, we know there is a solution to the equation ax+nq=b
if and only if gcd(a,n) | b. This means that there is a solution to
the congruence ax
b (mod n), then we can write ax+nq=b for some integer q. From a result
on diophantine equations, we know there is a solution to the equation ax+nq=b
if and only if gcd(a,n) | b. This means that there is a solution to
the congruence ax  b (mod n)
if and only if gcd(a,n) | b.
b (mod n)
if and only if gcd(a,n) | b.
In one of the examples above we got one solution from 0,1,2,3,
and for another we got two solutions from 0,1,2,3. How do we know how
many solutions we will get in this range, and how can we be sure
we have found them all? Let's think about the diophantine equations again.
We can write 2 x  8 (mod 4) as
2x+4y=8 for some integer y. Now dividing by 2, we find that we get
x+2y=4, that is x
8 (mod 4) as
2x+4y=8 for some integer y. Now dividing by 2, we find that we get
x+2y=4, that is x  4 (mod 2).
We might have thought that we could cancel to get x
4 (mod 2).
We might have thought that we could cancel to get x
 4 (mod 4), but that would have
meant that we missed some possible values of x - all those congruent to 2
modulo 4. What we should do is divide by 2 thoughout:
2x/2
4 (mod 4), but that would have
meant that we missed some possible values of x - all those congruent to 2
modulo 4. What we should do is divide by 2 thoughout:
2x/2  8/2 (mod
4/2). We summarise in the following result.
8/2 (mod
4/2). We summarise in the following result.
If ax  ay (mod an), then
x
ay (mod an), then
x  y (mod n).
y (mod n). 
Find all values of x which satisfy the congruence 5x  10 (mod 15).
10 (mod 15).
As gcd(5,15)=5 is a factor of 10, there are solutions. We divide by 5 to get
x  2 (mod 3). This gives the
following values for x (mod 15): 2,5,8,11,14.
2 (mod 3). This gives the
following values for x (mod 15): 2,5,8,11,14.
Find all values of x which satisfy the congruence 5x  10 (mod 18).
10 (mod 18).
As gcd(5,18)=1 is a factor of 10, there are solutions. We write the
congruence as a diophantine equation: 5x+18y=10, where x and y are integers.
By inspection, we see that a solution is given by x=-16 and y=5, and so the
general solution is x=-16+18t, y=5-5t, for integers t. So
x=-16+18t  -16
-16  2(mod 18).
2(mod 18).

Suppose we have ax  b (mod n)
and we can find an integer r so that
ar
b (mod n)
and we can find an integer r so that
ar  1 (mod n). Then we have
rax
1 (mod n). Then we have
rax  rb (mod n) and so
x
rb (mod n) and so
x  rb (mod n) as ar
rb (mod n) as ar  1 (mod n). When does such an integer r exist? It
exists if there is a solution to ar=1 + kn (integer k). There is a solution
exactly when gcd(a,n) | 1, that is, when gcd(a,n)=1. This is summarised in
the following result.
1 (mod n). When does such an integer r exist? It
exists if there is a solution to ar=1 + kn (integer k). There is a solution
exactly when gcd(a,n) | 1, that is, when gcd(a,n)=1. This is summarised in
the following result.
Suppose ax  b (mod n), where
gcd(a,n)=1. Then there is an integer r such that ar
b (mod n), where
gcd(a,n)=1. Then there is an integer r such that ar  1 (mod n) and
x
1 (mod n) and
x  rb (mod n).
rb (mod n).

One question which may arise is why, when we divided by a, did we divide everything by a:
 ay (mod an)
ay (mod an)
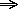 x
x y (mod n)
y (mod n)
but when we multiplied by r, we didn't multiply the modulus by r:
 b (mod n)
b (mod n)
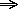 rax
rax  rb (mod n)?
rb (mod n)?The answer is as follows. First we write the congruence as a diophantine
equation: ax  b (mod n) becomes
ax+yn=b where y is an integer. Now we multiply by r to get rax+ryn=rb.
Now as ryn is divisible by n, it is congruent to 0 modulo n. Hence
rax
b (mod n) becomes
ax+yn=b where y is an integer. Now we multiply by r to get rax+ryn=rb.
Now as ryn is divisible by n, it is congruent to 0 modulo n. Hence
rax  rb (mod n), as required.
rb (mod n), as required.
If a  b (mod mn) then
a
b (mod mn) then
a  b (mod n) and
a
b (mod n) and
a  b (mod m)
b (mod m)
Find all values of x which satisfy the congruence 5x  10 (mod 18).
10 (mod 18).
As gcd(5,18)=1, there is an integer r such that
5r  1 (mod 18).
To find r, we either solve the diophantine equation 5r+18y=1, or we use
trial and error. Take r=-7, to get 5(-7)=-35
1 (mod 18).
To find r, we either solve the diophantine equation 5r+18y=1, or we use
trial and error. Take r=-7, to get 5(-7)=-35  1 (mod 18). Now we apply the result above to
5x
1 (mod 18). Now we apply the result above to
5x  10 (mod 18) to get
x
10 (mod 18) to get
x  -70
-70
 2 (mod 18).
2 (mod 18).
 5 (mod 9)
5 (mod 9)
 5 (mod 8)
5 (mod 8)
 8 (mod 12)
8 (mod 12)
 5 (mod 29)
5 (mod 29)
Now that we have covered solving individual congruences, we look at solving simultaneous congruences. Again, we rely on the techniques we developed earlier to solve diophantine equations.
Consider x  5 (mod 12) (*) and
x
5 (mod 12) (*) and
x  7 (mod 16) (**). From result 3
above, we know that x
7 (mod 16) (**). From result 3
above, we know that x  5 (mod 12)
5 (mod 12)
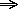 x
x  5 (mod 2) and
x
5 (mod 2) and
x  5 (mod 3) and
x
5 (mod 3) and
x  5 (mod 4)
and
x
5 (mod 4)
and
x  5 (mod 6). Similarly
x
5 (mod 6). Similarly
x  7 (mod 16)
7 (mod 16)
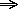 x
x  7 (mod 2) and
x
7 (mod 2) and
x  7 (mod 4)
and
x
7 (mod 4)
and
x  7 (mod 8). So
x
7 (mod 8). So
x  5
5 1 (mod 4) and
x
1 (mod 4) and
x  7
7  3 (mod 4), which is a contradiction. Hence there are no solutions to
this pair of simultaneous equations.
3 (mod 4), which is a contradiction. Hence there are no solutions to
this pair of simultaneous equations.
Solve the simultaneous congruences
x  5 (mod 12) and
x
5 (mod 12) and
x  3 (mod 5).
3 (mod 5).
 17 (mod 60).
17 (mod 60). 5 (mod 12)
and x=17-60u
5 (mod 12)
and x=17-60u 2 (mod 5),
which is correct.
2 (mod 5),
which is correct. 5 (mod 9) and
x
5 (mod 9) and
x  7 (mod 13)
7 (mod 13)
 11 (mod 12) and
x
11 (mod 12) and
x  12 (mod 13)
12 (mod 13)
 5 (mod 12) and
5x
5 (mod 12) and
5x  7 (mod 13)
7 (mod 13)
 4 (mod 12) and
x
4 (mod 12) and
x  7 (mod 26)
7 (mod 26)
 5 (mod 12) and
x
5 (mod 12) and
x  7 (mod 26)
7 (mod 26)