
Diskret matematik A för datateknik
Examination Questions from 1999-08-25
Question 1 (8p)
Choose the correct option(s) for each of the following, giving a short explanation of your choice. You may quote theorems and definitions in your explanation.
- The number of ways to order the letters in the word MATEMATIK is
- 9(7!)
- 9!
- 9!/(2!2!2!)
- none of the above
- A set X is countable if
- it is a subset of
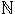 .
.
- there is an injection from X to
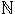 .
.
- there is a bijection from X to
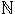 .
.
- there is a surjection from X to
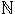 .
.
-
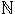 is a subset of X.
is a subset of X.
- none of the above.
- For integers k
 1,
1,
| ( | 2k
1 |
) |
+ |
( | 2k
2 |
) |
+ |
( | 2k
3 |
) |
+ | ... | + |
( | 2k
k |
) |
is equal to
- 22k-1-2
- 2n
- 2k-1
- 22k-1-1
- none of the above
- Two graphs G and G' are isomorphic if
- they have the same number of vertices.
- they have the same number of edges.
- their complements are isomorphic.
- they contain no triangles
- none of the above
- If two graphs G and G' are isomorphic then
- they have the same number of vertices.
- they have the same number of edges.
- their complements are isomorphic.
- they contain no triangles
- none of the above
- In a land far far away, live two types of elves.
Each elf is either a light elf or a dark elf.
The only difference between the two types of elves is
whether they tell the truth all the time, or lie all
the time. Unfortunately the situation is further complicated by
insanity. A light elf always tells the truth as he sees it.
This means that a sane light elf tells the truth, but an insane light
elf lies. Similarly a dark elf always lies as he sees it so
an insane dark elf always tells the truth and a sane dark elf
always lies.
One of Elvina and Falina is a light elf the other is a dark elf.
You have the following information.
Elvina: We are both insane.
You: Is that true?
Falina: Of course not.
Which of the following are correct?
- Elvina is a dark elf and Falina is a light elf.
- Falina is a dark elf and Elvina is a light elf.
- Both are sane
- Both are insane
- Both are sane or both are insane
- one is sane and one is insane
- insufficient information to deduce anything
- none of the above
- For sets X={1,2,3}, Y={4,{5,1}, 2} which
of the following are correct?
- X
 Y={1,2}
Y={1,2}
- {5,1}
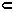 Y
Y
- {4, {1,5}}
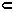 Y
Y
- 1
 Y
Y
- None of the above
Question 2 (4p)
I am going to make a crocheted blanket (afghan).
For the afghan, I need
two different colours of wool. I have found two that I like, but
unfortunately they come in different sized balls. The blue
wool comes in 450g balls and the green wool
comes in 200g balls.
I need a total of 3250g of wool for my project. As there is a
limited number of balls of each colour available, and the
wool is expensive, I need to know all feasible solutions so
that I wont buy too much or too little of each.
Only whole balls may be purchased. Can you help?
I need to know all the possible solutions, and how you obtained
them - you must convince me that your answer is correct. I don't
want to spend hours working on this blanket, to find I have the
wrong quantity of wool because you made a mistake!
Question 3 (5p)
- State and prove a formula which gives a relationship between
the number of edges in a graph and the degrees of the vertices.
- Describe how and why proof by contradiction works.
- Prove that every tree contains at least one vertex of degree one.
(Hint: Let T be a tree on n vertices.
Suppose that it does not have a vertex of degree 1. What degrees
are possible for the vertices? Why?
How many edges does T have?)
Question 4 (4p)
- Define chromatic index and chromatic number.
- Find the chromatic number and chromatic index for each of the
following graphs. You should prove your results.
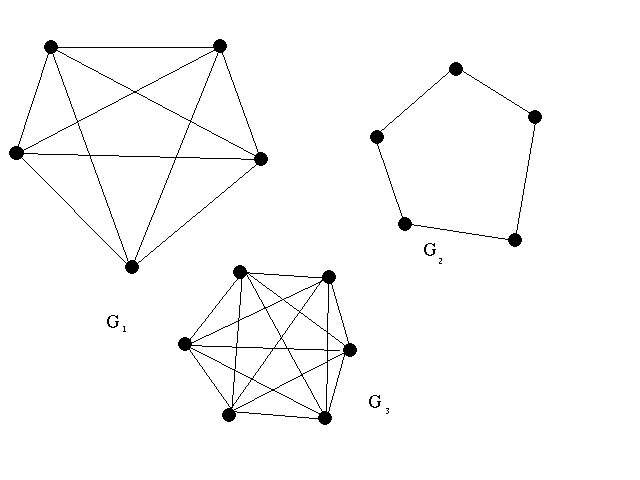
Question 5 (4p)
Suppose the numbers 1,2,3,...,20 are arranged around a
dart board and that we know the sum a+b+c+d of every set
{a,b,c,d} of four consecutive numbers around the
board. Is it possible that none of these sums is more
than 40? Prove your result.
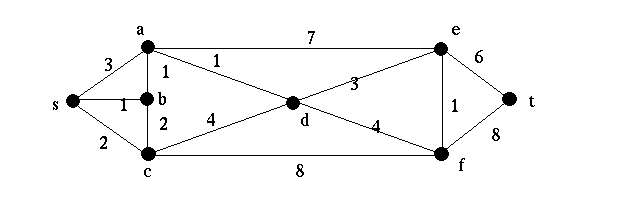
Question 5 (7p)
- Find a shortest path in the following graph between
s and t. You should explain your method.
- Find a minimum spanning tree in the graph below. Explain
your method.
- Does the minimum spanning tree give a shortest route
from s to t? If it does, is this always the case?
Sarah Norell
© MITTHÖGSKOLAN
Institutionen för Fysik och Matematik
Mitthögskolan
SE-851 70 SUNDSVALL
Sweden
Updated 000222.


 .
.
 .
.
 .
.
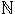 .
.
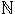 is a subset of X.
is a subset of X.
 1,
1,
 Y={1,2}
Y={1,2}
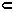 Y
Y
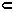 Y
Y
 Y
Y

