Recall that we looked at the size of the set AxB, that is the cartesian product of A and B (it consists of pairs (a,b) where a
 A and b
A and b  B.)
We saw that the cardinality |AxB| = |A| |B|. This is the Multiplication Principle for two sets.
B.)
We saw that the cardinality |AxB| = |A| |B|. This is the Multiplication Principle for two sets.
We continue our discussions about functions this week by considering invertible discrete functions, and we shall also discuss the magnitude of functions and basic complexity theory.
In the combinatorics section we will be concerned with answering
'how many'-type questions. We have met the fundamental principles for answering
this type of question earlier in the course: The Multiplication Principle and the Addition
Principle.
Recall that we
looked
at the size of the set AxB, that is the cartesian product of A and B (it
consists of
pairs (a,b) where a  A and b
A and b  B.)
We saw that the cardinality |AxB| = |A| |B|. This is the Multiplication Principle for two sets.
B.)
We saw that the cardinality |AxB| = |A| |B|. This is the Multiplication Principle for two sets.
Click here for an English version.
För att få bonuspoängen måste du lämna in ett bra
försök på alla
frågorna innan
onsdagen den 17 maj, kl 8:00.
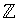
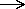
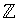 där f(n)=7n+3.
där f(n)=7n+3.
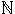
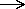
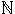 där g(n)=n+7.
där g(n)=n+7.
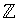
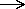
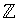 där h(n)=n+7.
där h(n)=n+7.