Discrete Mathematics B
Old exam: 2000-01-08
TENTAMEN I MATEMATIK
DISKRET MATEMATIK B FÖR DATATEKNIK
Datum: 2000-1-8
Skrivtid: 5h
Hjälpmedel: Inga
Vincent Moulton, Mitthögskolan
Lösningarna skall vara presenterade på ett sådant sätt
att räkningar och
resonemang blir lätta att följa.
Ett svar utan motivering ger 0 poäng!
1.
Are the following statements true or false? Explain
your answer!
(a) The number of partitions S(7,3) of a 7-set into
3 parts is equal to 305.
(b) The permutation
is even.
(c) The remainder when 336 is divided by
17 is 5.
(d) There are three mutually non-isomorphic trees with
5 vertices.
(e) The coefficient of x5y2z3 in
(x+y+z)10
is 1031.
(f) It is possible to find a design with
parameters (7,2,3).
(9p)
2.
Give a combinatorial argument using sets
to show that
for
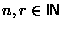 ,
,
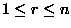 .
(4p)
.
(4p)
3.
How many ways are there to arrange the
letters
K E D H M Å J
(a) in a sequence?
(b) in a sequence that contains the word HEJ?
(c) in a sequence that does not contain either of
the words HEJ and DÅ?
(3p)
4.
(a) Find the first five terms in the
sequence
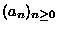 defined by a0=1, a1= 1, and
defined by a0=1, a1= 1, and
(b) Find a formula for an. Check your answer using (a).
(4p)
5.
Do a breadth-first search (BFS) and a depth-first search (DFS)
on the graph which has the following adjacency list:
| a |
b |
c |
d |
e |
f |
g |
h |
i |
| b |
d |
e |
b |
c |
e |
h |
g |
g |
| |
c |
f |
e |
d |
c |
i |
|
|
| |
|
b |
g |
f |
|
|
|
|
Is this graph connected?
(4p)
6.
Let
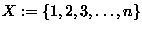 ,
,
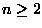 .
Consider the
following algorithm:
.
Consider the
following algorithm:
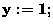 for each non-empty subset
for each non-empty subset 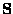 of
of 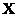 do
do
begin

end;
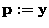
(a) If n= 4, then what will the
output p be?
(b) If we take * as the significant operation
in the loop, then what is the
efficiency of this algorithm in terms of n?
(c) If we replace the second line of the
algorithm by
for each 2-subset 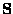 of
of 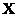 do
do
then what is the
efficiency of this new algorithm in terms of n?
(4p)
7.
(a) Without using generating functions,
find the number of integer solutions to
x1 + x2 + x3 + x4 + x5 = 11
where
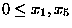 ,
and
,
and
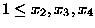 .
.
(b) Explain why the answer you got for (a)
is equal to the coefficient of x11 in
(c) Show that
(d) Use the formula in (c) to find the
coefficient of x11 in f(x).
(4p)
TENTAMEN I MATEMATIK
DISKRET MATEMATIK B FÖR DATATEKNIK
Datum: 2000-1-8
Skrivtid: 5h
Hjälpmedel: Inga
Vincent Moulton, Mitthögskolan
Lösningarna skall vara presenterade på ett sådant sätt
att räkningar och
resonemang blir lätta att följa.
Ett svar utan motivering ger 0 poäng!
1.
Är följande påståenden sanna eller falska?
Motivera dina svar!
(a) Antalet partitioner S(7,3) av en 7-mängd i
3 delar är 305.
(b) Permutationen
är jämn.
(c) Resten när 336 delas med
17 är 5.
(d) Det finns tre inbördes icke-isomorfa träd med
5 hörn.
(e) Koefficienten framför x5y2z3 i
(x+y+z)10
är 1031.
(f) Det är möjligt att hitta en design med parametrar
(7,2,3).
(9p)
2.
Ge ett kombinatoriskt argument
med mängder för att visa att
för
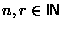 ,
och
,
och
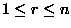 .
(4p)
.
(4p)
3.
På hur många sätt kan man arrangera
bokstäverna
K E D H M Å J
(a) i en följd?
(b) i en följd som inhåller ordet HEJ?
(c) i en följd som inte
innehåller något av orden HEJ och DÅ?
(3p)
4.
(a) Hitta de första fem termerna i följden
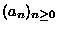 definierad av a0=1, a1= 1, och
definierad av a0=1, a1= 1, och
(b) Hitta en formel för an. Kontrollera ditt svar
genom att avända (a).
(4p)
5.
Gör en bredd-före-djup sökning (BFS) samt en djup-före-bredd sökning (DFS)
till grafen som har följande grannlista:
| a |
b |
c |
d |
e |
f |
g |
h |
i |
| b |
d |
e |
b |
c |
e |
h |
g |
g |
| |
c |
f |
e |
d |
c |
i |
|
|
| |
|
b |
g |
f |
|
|
|
|
Är denna graf sammanhängande?
(4p)
6.
Låt
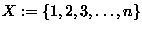 ,
,
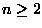 .
Betrakta algoritmen:
.
Betrakta algoritmen:
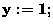 for varje icke-tom delmängd
for varje icke-tom delmängd 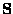 av
av 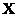 do
do
begin

end;
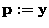
(a) Om n= 4, vad blir utdata p?
(b) Om * är loopens signifikanta operation,
vad är algoritmens effektivitet i
termer av n?
(c) Om vi byter ut algoritmens andra rad mot
for varje 2-delmängd 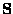 av
av 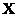 do
do
vad blir effektiviteten hos den nya algoritmen?
(4p)
7.
(a) Utan att använda genererande funktioner, hitta antalet
heltalslösningar till
x1 + x2 + x3 + x4 + x5 = 11
där
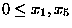 ,
och
,
och
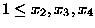 .
.
(b) Förklara varför ditt svar i (a)
är lika med koefficienten för x11 i
(c) Visa att
(d) Använd formeln i (c) för att hitta koefficienten
för x11 i f(x).
(4p)
Vincent Moulton
© 2000, MITTHÖGSKOLAN
Institutionen för Fysik och Matematik
Mitthögskolan
SE-851 70 SUNDSVALL
Sweden
Updated 000412.
![]() defined by a0=1, a1= 1, and
defined by a0=1, a1= 1, and
![]() ,
,
![]() .
Consider the
following algorithm:
.
Consider the
following algorithm:
![]()
![]()
![]() definierad av a0=1, a1= 1, och
definierad av a0=1, a1= 1, och
![]() ,
,
![]() .
Betrakta algoritmen:
.
Betrakta algoritmen:
![]()
![]()