
MAAB16 Discrete Mathematics B
Unit 0: Foundations
Unit 0: Foundations
 |
Unit 0: Foundations |
A limited amount of new material is being covered in this preliminary unit. The purpose of Unit 0 is to revise what you have learnt about integers, divisibility and finite arithmetic on your Discrete Mathematics A course. Two of your most important theorems from Discrete Mathematics A are the Division Theorem and the Fundamental Theorem of Arithmetic. We did not prove these two theorems on Discrete Mathematics A, so we prove them now.
We shall also revise equivalence relations, and in particular the congruence modulo n relation. We covered the basic rules of arithmetic modulo n on Discrete Mathematics A, including their proofs, and you have learnt how to solve congruences modulo n. We shall revise these rules and learn two further useful rules for modular arithmetic which were not covered on Discrete Mathematics A. They are known as Fermat's Little Theorem and Euler's Theorem.
References to [Biggs] are given for all the revision material rather than to your Discrete Mathematics A coursebook. This is done so that you will be able to familiarise yourself with Biggs' style of writing and his terminology by reading material well-known to you already.
If you feel a need to refresh your memory w.r.t. the proof techniques you have learnt on your Discrete Maths A course, you can read chapters 1 - 3 in [Biggs]. He covers most of what you have learnt. I give a short description of what is covered by each section and suggest some good exercises, that will test if you understand the material. Remember that solutions to all exercises in [Biggs] are available via the link on the course homepage. However, make sure that you attempt to solve the exercises yourself before looking up the solution. Remember that being able to understand the solution of someone else, does not ensure that you would be able to solve a similar exercise yourself in the future. It is important to have thought about a problem and tried various ways of solving it beforehand, only then will a solution be beneficial in that it hopefully makes the last few pieces of the puzzle fall into place.
Section 1.1 explains what a mathematical statement is and gives some examples.
Section 1.2 is an important section that everybody is advised to read. It contains hints about how to attack and solve mathematical problems in the form of some exercises with analytical discussions. Everybody should thus have a good look at Exercises 1.2.2 - 1.2.6.
Section 1.3 covers compound statements using AND and OR. Two good revision exercises are Exercises 1.3.2 + 1.3.3.
Sections 1.4-1.6 are about statements containing quantifiers
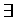 and
and 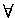 . This is also
discussed further in Section 3.6 (see below). One important thing revised in these three sections
is that an example can be used to prove an existence and a counter-example can be used to disprove
a universal statement. One very common error is to attempt to 'prove' a universal statement by
an example. Be sure that you understand why this cannot be done. Good revision exercises to try are
Exercises 1.4.4, 1.4.5, 1.5.2, 1.5.3, 1.5.4, 1.6.2, 1.6.4, 1.7.3, 1.7.6.
. This is also
discussed further in Section 3.6 (see below). One important thing revised in these three sections
is that an example can be used to prove an existence and a counter-example can be used to disprove
a universal statement. One very common error is to attempt to 'prove' a universal statement by
an example. Be sure that you understand why this cannot be done. Good revision exercises to try are
Exercises 1.4.4, 1.4.5, 1.5.2, 1.5.3, 1.5.4, 1.6.2, 1.6.4, 1.7.3, 1.7.6.
Sections 2.1-2.3 are about basic set notation. It also describes some universal sets.
In particular the natural numbers
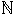 = {1,2,3, ...}
= {1,2,3, ...} = {... ,-2, -1, 0, 1, 2, 3, ...}
= {... ,-2, -1, 0, 1, 2, 3, ...} 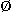 , which denotes the empty set { }.
Next he combines sets using the union and intersection operations. It is important
to know the associative and distributive laws for these operations. In one of the exercises, set difference is covered
also.
Good revision exercises to try are
Exercises 2.1.1, 2.1.3, 2.2.2, 2.2.3, 2.3.1, 2.3.3, 2.3.4.
, which denotes the empty set { }.
Next he combines sets using the union and intersection operations. It is important
to know the associative and distributive laws for these operations. In one of the exercises, set difference is covered
also.
Good revision exercises to try are
Exercises 2.1.1, 2.1.3, 2.2.2, 2.2.3, 2.3.1, 2.3.3, 2.3.4.
Section 3.3-3.4 introduces the if-then statement. It is important to understand that just because
the statement p 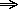 q is true it does not necessarily mean that
the converse statement q
q is true it does not necessarily mean that
the converse statement q 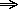 p is also true. Section 3.4 discusses this kind
of statements. Make sure you always think twice about whether any given statement is an if-then
statement or an if and only if-statement. It is a very common mistake to confuse the two. Good revision exercises to try are
Exercises 3.4.1, 3.4.2.
p is also true. Section 3.4 discusses this kind
of statements. Make sure you always think twice about whether any given statement is an if-then
statement or an if and only if-statement. It is a very common mistake to confuse the two. Good revision exercises to try are
Exercises 3.4.1, 3.4.2.
Section 3.5 is about the important contrapositive statement
of p 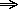 q. It is
important to be able to state the contrapositive statement of
any p
q. It is
important to be able to state the contrapositive statement of
any p 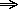 q statement, as it is often easier to
prove this than proving p
q statement, as it is often easier to
prove this than proving p 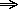 q directly.
Good revision exercises to try are
Exercises 3.5.1, 3.5.2, 3.5.3, 3.5.4.
q directly.
Good revision exercises to try are
Exercises 3.5.1, 3.5.2, 3.5.3, 3.5.4.
Section 3.6 has more about statements containing quantifiers
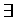 and
and 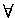 . This
time in a more formal setting than in Chapter 1.
Good revision exercises to try are
Exercises 3.6.1, 3.6.2. Some further good revision exercises can be found in Section 3.7:
Exercises 3.7.1, 3.7.7, 3.7.8, 3.7.9.
. This
time in a more formal setting than in Chapter 1.
Good revision exercises to try are
Exercises 3.6.1, 3.6.2. Some further good revision exercises can be found in Section 3.7:
Exercises 3.7.1, 3.7.7, 3.7.8, 3.7.9.
Sections 4.1-4.6 in [Biggs] revises some of what you learnt in Discrete Maths A about the natural numbers, and sections 7.1-7.3 revises what we know about integers. We describe the contents of the sections here and leave it up to you to decide what you need to revise in order to have a good understanding of the topics covered.
Section 4.1 contains the basic axioms for the natural numbers, which together make up most of the well-known
rules of arithmetic for 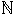 that you are used to and have been working with for many years.
They are presented here in a slightly more formal language than you will be used to from your
schooldays, but none of the rules are unknown to you, and you have gradually learnt more and more formal
mathematical language, so you will have no problem in reading and
understanding them. Theorem 4.1 is the important result that any common divisor (Swedish: gemensam delare)
of two natural numbers
a and b divides any linear combination of a and b. We proved this in Discrete Maths A
for all integers, not just
natural numbers. Exercise 4.1.2 is a good revision exercise.
that you are used to and have been working with for many years.
They are presented here in a slightly more formal language than you will be used to from your
schooldays, but none of the rules are unknown to you, and you have gradually learnt more and more formal
mathematical language, so you will have no problem in reading and
understanding them. Theorem 4.1 is the important result that any common divisor (Swedish: gemensam delare)
of two natural numbers
a and b divides any linear combination of a and b. We proved this in Discrete Maths A
for all integers, not just
natural numbers. Exercise 4.1.2 is a good revision exercise.
In Section 4.2 Biggs introduces the '<'-relation on 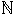 . He does
this by defining that m < n means there is a natural number x
such that m+x=n. This does not
conflict with our intuitive understanding of '<' from our schooldays, as we can just interprete this as
n being x steps further to the right on the 'number line' than m, so it is easy enough to
accept. He goes on to formally prove that the '<'-relation is transitive on
. He does
this by defining that m < n means there is a natural number x
such that m+x=n. This does not
conflict with our intuitive understanding of '<' from our schooldays, as we can just interprete this as
n being x steps further to the right on the 'number line' than m, so it is easy enough to
accept. He goes on to formally prove that the '<'-relation is transitive on
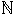 . We covered transitive relations on Discrete Maths A, but if you have forgotten
about them, you can get to know them again by reading [Biggs] Section 7.2 (see below).
. We covered transitive relations on Discrete Maths A, but if you have forgotten
about them, you can get to know them again by reading [Biggs] Section 7.2 (see below).
In Section 4.3 proof by induction is revised. This proof method is important in discrete mathematics, where
we often want to
prove that some proposition holds for all n 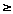 b, where b is
some fixed base number. Make sure
you remember how to do a proof by induction. Good revision problems
can be found in Exercises 4.3.1, 4.3.2, 4.4.1.
b, where b is
some fixed base number. Make sure
you remember how to do a proof by induction. Good revision problems
can be found in Exercises 4.3.1, 4.3.2, 4.4.1.
In Section 4.4 Biggs revises summation notation and some standard sums like
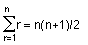
In Section 4.5 Biggs revises how to define a sequence by a recurrence relation and an initial term. You will recall from Discrete Maths A that we can often guess a closed expression for the general term of such a sequence and subsequently use induction to prove that our guess is right.
In Section 4.6 Biggs introduces the Principle of Strong Induction. This is equivalent to
the Principle of Induction with which you are familiar. You will recall that induction is a sort of domino-effect,
where we first prove that we can knock over an initial domino. We then assume that somebody
has knocked over domino k, where k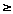 1 is some fixed, but random
natural number. From this assumption and the base we then prove that we can knock over domino k+1. We finally conclude
that because domino 1 falls and whenever k falls, then k+1 falls too, then the statement holds for all
n
1 is some fixed, but random
natural number. From this assumption and the base we then prove that we can knock over domino k+1. We finally conclude
that because domino 1 falls and whenever k falls, then k+1 falls too, then the statement holds for all
n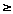 1.
1.
The Principle of Strong Induction describes the same domino-effect, but in a slightly different way:
Again we start by proving that we can knock over the first domino. We then assume that somebody
has knocked over all dominos with numbers n 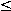 k, where k is as before.
As before we then prove that this makes domino k+1 fall too, and we may conclude that all dominos fall
because number 1 makes number 2 fall; number 1 and 2 in turn make number 3 fall, numbers 1,2 and 3 make
number 4 fall, etc. We have in fact used strong induction on Discrete Maths A a number
of times. E.g. when we proved that a tree with n vertices has n-1 edges. A good exercise to try
is Exercise 4.6.3.
k, where k is as before.
As before we then prove that this makes domino k+1 fall too, and we may conclude that all dominos fall
because number 1 makes number 2 fall; number 1 and 2 in turn make number 3 fall, numbers 1,2 and 3 make
number 4 fall, etc. We have in fact used strong induction on Discrete Maths A a number
of times. E.g. when we proved that a tree with n vertices has n-1 edges. A good exercise to try
is Exercise 4.6.3.
Section 4.7 contains the first really new material on this course. The section starts with the definition
of what is meant by the maximum and the minimum of a subset X of the natural numbers 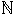 .
It is important to understand that not every subset of
.
It is important to understand that not every subset of 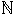 has a
maximum. In Exercise 4.7.1
for example, it is proven that
has a
maximum. In Exercise 4.7.1
for example, it is proven that 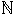 itself has no maximum number. Do this exercise!
itself has no maximum number. Do this exercise!
At the other end, however, Theorem 4.7 proves that every non-empty subset X of the natural numbers has a least element . This is an extremely important property of the natural numbers which is used many times in proofs in both this and other mathematics courses.
The proof of Theorem 4.7 is by induction. The
induction itself is not that hard to understand, but the statement proven is perhaps not quite what
you would expect, so let us discuss it.
Biggs proves by induction for all n 
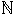 that
that
 X THEN X has a least number.
X THEN X has a least number. In Section 7.1 Biggs introduces the set of negative integers.
Section 7.2 is a revision of the basics about relations on sets and their properties. Make sure you understand what it means for a relation to be reflexive, symmetric and transitive. Also the notion of an equivalence relation is revised. Good revision exercises are Exercises 7.2.1, 7.2.3
Section 7.3 is about the equivalence classes of a relation R on a set X. It is important to understand that the equivalence classes of an equivalence relation R on a set X partition X. We mentioned this on your Discrete Maths A course, but we did not prove it, so it is important that you read the proof now. You prove this by showing that
Now go to Section 7.6 which also contains new material. Here Biggs starts by defining what is meant by a lower bound for a
subset X of the integers.
It is important to understand that the lower bound of X is not necessarily a member of X.
It is equally important to understand
that not every subset of  has a lower bound.
has a lower bound.  itself, for example, has no lower bound.
itself, for example, has no lower bound.
Theorem 7.6 then assures that if a non-empty subset S of  has a
lower bound, then S has a least member. We saw in Section 4.7 that any subset of
has a
lower bound, then S has a least member. We saw in Section 4.7 that any subset of 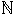 has a least element. This is used in the proof of Theorem 7.6, which you should read carefully.
Good exercises are Exercises 7.6.2, 7.6.3, 7.7.7.
has a least element. This is used in the proof of Theorem 7.6, which you should read carefully.
Good exercises are Exercises 7.6.2, 7.6.3, 7.7.7.
Section 8.1 revises multiples, factors and the notation 'x|y' which means 'x divides y'.
Note that this relation is not a symmetric relation on  as
e.g.
as
e.g.
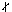 2.
2. Section 8.2 is about the Division Theorem (also called the Division Algorithm). We saw several important applications of this on your Discrete Maths A course (e.g. see Section 8.3 about number bases). Thus we now want a proof of this essential theorem. The basic statement of the result is in Theorem 8.2. However, it is important also to understand that the quotient and remainder found by the theorem are unique. Biggs remarks this after the proof of the theorem.
Study the proof of Theorem 8.2 carefully:
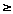 0.
0.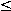 b-1, which is done by contradiction.
b-1, which is done by contradiction.Section 8.4 revises the definition of the greatest common divisor of two inegers a and b and Euclid's algorithm, which can be used to find gcd(a,b). The most important result is Theorem 8.4 which is the one guaranteeing that gcd(a,b) can be written as a linear combination of a and b. The proof given is basically the same as the one we studied on Discrete Maths A, namely that by working backwards in Euclid's Algorithm we can obtain the required linear combination. We shall use this result later on in the unit for another important proof, so make sure you read the proof thoroughly. Good revision exercises are Exercises 8.4.2, 8.4.3.
At the end of Section 8.4 Biggs defines two integers a and b to be coprime if gcd(a,b) =1. Note that if a and b are coprime then Theorem 8.4 gives you that there are integers m and n such that ma+nb=1. We shall need this result later in the unit in the proof of Theorem 13.3.1.
In Section 8.5 Biggs revises the definition of primes and composite integers.
Section 8.6 is devoted to proving the Fundamental Theorem of Arithmetic, which we also introduced on Discrete Maths A, but did not prove. This is an important result which is used often, so we now prove it.
The proof is in two parts. Firstly, in Theorem 8.6.1 it is proved by induction that if a prime p divides a product of n integers then p divides (at least one) of the integers. The base for n=1 is trivial. For n=2 we proved the result on Discrete Maths A, so look it up in your notes, if you have problems with the proof. The proof in [Biggs] is virtually identical to the one you saw on Discrete Maths A. The result for n=2 forms the major part of the induction step.
After proving Theorem 8.6.1 it is clear that every integer has a prime factorization. What remains to be proven is that the factorization is unique. This is done by assuming that we have two different prime factorizations of the same integer and then showing that they consist of exactly the same primes, though possibly in a different order.
Exercises 8.6.1, 8.6.3, 8.7.9 are recommended revision exercises.
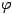 -function
-functionYou will recall that at the end of Section 8.4 Biggs defined what it means for two integers
a and b to be coprime. Euler's 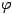 -function is concerned with
such integers.
For any n
-function is concerned with
such integers.
For any n 
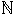 we define
we define
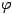 (n) to be
the number of positive integers x < n which are coprime with n.
To get a feel for the
(n) to be
the number of positive integers x < n which are coprime with n.
To get a feel for the 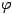 -function, start by computing
-function, start by computing
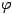 (1),
(1), 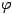 (2),
(2),
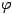 (3), ... ,
(3), ... , 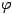 (10). Then read
[Biggs] Section 10.3. Compare your results with the table in the beginning of the section.
(10). Then read
[Biggs] Section 10.3. Compare your results with the table in the beginning of the section.
Note that any integer is coprime with 1 as gcd(a,1)=1 for any integer a.
Next it is easy to see that 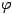 (p) = p-1 when p is a prime. This follows
directly from the definition of prime numbers as the only natural number x < p dividing the prime p
is 1, so p must be coprime with the other p-2 numbers also.
(p) = p-1 when p is a prime. This follows
directly from the definition of prime numbers as the only natural number x < p dividing the prime p
is 1, so p must be coprime with the other p-2 numbers also.
Theorem 10.3 is an interesting property of Euler's 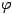 -function.
Use this result and the function values you computed above to compute
-function.
Use this result and the function values you computed above to compute 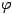 (20).
Exercise 10.3.4 is recommended.
(20).
Exercise 10.3.4 is recommended.
Section 13.1 defines a 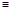 b (mod n) in the same
way as we
did on Discrete Maths A, namely a
b (mod n) in the same
way as we
did on Discrete Maths A, namely a 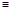 b (mod n) when
n | (a-b). Biggs then goes on to prove the rules of arithmetic
for congruence modulo n which we also proved on Discrete Maths A. Make sure you can apply the rules in practical
computations
and that you know how to prove them too.
b (mod n) when
n | (a-b). Biggs then goes on to prove the rules of arithmetic
for congruence modulo n which we also proved on Discrete Maths A. Make sure you can apply the rules in practical
computations
and that you know how to prove them too.
Section 13.2 defines  n, i.e. the set of congruence
classes modulo n. Subsequently
the familiar operations of addition
n, i.e. the set of congruence
classes modulo n. Subsequently
the familiar operations of addition 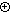 and
multiplication
and
multiplication 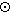 on
on  n are defined.
n are defined.
Notice that Biggs goes over to using a different notation for congruence classes and arithmetic in
 n. E.g. he writes
n. E.g. he writes
 3
3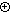 [2]3 = [0]3
[2]3 = [0]3  n
as it is important for what follows in the next section. Try Exercises 13.1.1, 13.2.1, 13.2.2, 13.2.3
n
as it is important for what follows in the next section. Try Exercises 13.1.1, 13.2.1, 13.2.2, 13.2.3
Section 13.3 starts with the definition of what it means for an element
of  n
to have a (multiplicative) inverse: [r]n has a multiplicative inverse if there is some
[x]n
n
to have a (multiplicative) inverse: [r]n has a multiplicative inverse if there is some
[x]n 
 n such that
n such that
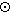 [x]n =
[x]n
[x]n =
[x]n 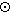 [r]n = [1]n.
[r]n = [1]n.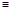 xr
xr 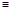 1 (mod n).
1 (mod n). n.
n.Next, Theorem 13.3.1 says:

 m
is invertible
m
is invertible 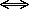 gcd(r,m) = 1.
gcd(r,m) = 1.The proof of 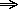 is not hard if you remember
that rx = 1 in
is not hard if you remember
that rx = 1 in  m
is the same as
m
is the same as
rx 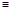 1 (mod m). This in turn gives
that m | (rx-1) such that
1 (mod m). This in turn gives
that m | (rx-1) such that

 .
. 
 by doing Euclid's
Algorithm backwards (Theorem 8.4).
by doing Euclid's
Algorithm backwards (Theorem 8.4).
Now recall Euler's 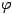 -function from Section 10.3. We have the following:
-function from Section 10.3. We have the following:
Corollary: 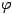 (m) is the number of invertible
elements in
(m) is the number of invertible
elements in  m.
m.
Next is Euler's Theorem (Theorem 13.3.2). It says that
if a 
 m is invertible, then
m is invertible, then
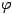 (m) = 1 in
(m) = 1 in  m.
m.It is crucial for the proof of Euler's Theorem that if Um denotes the set of invertible elements in
 m, then yUm = Um. Here
m, then yUm = Um. Here
 Um },
Um }, Recall that in order to prove that two sets A and B are equal we prove
A 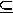 B and
B and
B 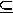 A. Hence Biggs proves
yUm
A. Hence Biggs proves
yUm 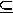 Um and
Um
Um and
Um 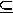 yUm.
yUm.
At the bottom of p. 148 Biggs claims that the inverse of u=x1x2...xk-1xk
is the element
u -1 = xk -1 ... x2 -1x1 -1. This is
easiest to see if you compute
The result known as Fermat's Little Theorem is a special case of Euler's Theorem with m=p where p is
a postive prime.
Since 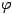 (p) = p-1 and
a
(p) = p-1 and
a 
 p
is invertible when gcd(a,p)=1, i.e. when p
p
is invertible when gcd(a,p)=1, i.e. when p 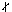 a we get:
a we get:
Fermat's Little Theorem: If p 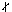 a then
ap-1
a then
ap-1 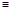 1 (mod p).
1 (mod p).
Exercises 13.3.4, 13.3.5, 13.3.6, 13.3.7 are recommended.
Q1. Find r1 
 such that
0
such that
0 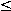 r1
r1 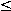 40 and
200441
40 and
200441 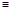 r1 (mod 41).
r1 (mod 41).
Q2. Find r2 
 such that
0
such that
0 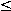 r2
r2 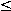 60 and
20046000
60 and
20046000 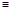 r2 (mod 61).
r2 (mod 61).