
MAAB16 Discrete Mathematics B
Unit 3: Partitions and Permutations
Unit 3: Partitions and Permutations
 |
Unit 3: Partitions and Permutations |
In this unit we shall look further at partitions and their connection with equivalence relations. We shall learn how to count the number of partitions of a set of size n into k parts. The number of these is the so-called Stirling number S(n,k). We shall give a recurrence relation for calculating Stirling numbers much like the one you saw for binomial coefficients in Pascal's triangle in Thm 11.1.1. We shall also see that the number of partitions of a set of size n into k parts are closely related to the number of ways of distributing n balls among k boxes such that no box is left empty. The investigation of these will lead us to the multinomial coefficients. After studying partitions of a set of size n into k parts, we consider the related partition of an integer n into a sum of k positive integers, and you shall learn how to use a Ferrers diagram to study such partitions.
Finally we shall return to studying permutations of a set of size n. We shall see that the disjoint cycle notation for permutations which we were introduced to in section 10.6 partitions the set of permutations Sn. The simplest pemutation of an n-set is a transposition, it swaps two elements of the set and leaves all the other n-2 elements fixed. We shall see that every permutation can be written as a composition of a number of transpositions and that this feature defines two classes of partitions, namely the odd permutations that can be written as a composition of an odd number of transpositions, and the even permutations which can be written as the composition of an even number of permutations.
Section 12.1 starts by defining what is meant by a family of sets. Make sure you understand the difference between a set and a family.
Example Let X1 = {1,2}, X2 = {2,3}, X3 = {1,2}, X4 = {2,3} and
X5 = {1,2}.
Then F={Xi | i 
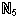 } is
a family of five sets even though some of the sets are the same.
} is
a family of five sets even though some of the sets are the same.
Next is the definition of a partition. We have studied this definition on your Discrete Maths A course, so this is just revision. It is important to note that the parts of a partition are non-empty.
The Stirling number S(n,k) is the number of partitions of a set of size n (also called an n-set) with precisely k parts. Finding a closed formula for this is quite hard, but Biggs proves a recurrence relation in Theorem 12.1 which enables us to compute S(n,k) for all n and k. The proof of Theorem 12.1 is very much like the one you learnt for Pascal's triangle in Theorem 11.1.1, which we studied in Unit 2. Recommended exercises are Exercises 12.1.1, 12.1.2.In Section 12.2 Biggs argues that a partition of a set X gives rise to an equivalence relation on X and vice versa. Biggs proved this already in section 7.2, which we discussed in Unit 0. It is important that you understand fully the connection between equivalence relations and partitions, so it may be a good idea to revise section 7.2 again at this point. Good exercises are Exercises 12.2.1, 12.2.2, 12.2.3, 12.2.4, 12.2.5.
Biggs starts Section 12.3 with interpreting partitions of an n-set into k parts as distributions of n items into k boxes such that there are no empty boxes. Distributions of n items into k boxes with no box empty corresponds to a surjective function from the set of items to the set of boxes. So the number of such distributions is the number of surjections from an n-set to a k-set. This leads to Theorem 12.3.1 where Biggs counts these surjections. Recall that we counted the number of functions from an n-set to a k-set in Theorem 10.4 and the number of injections in Theorem 10.5. It may be a good idea at this point to revise these two theorems at this point.
The multinomial coefficient
| ( | n
m1, m2, ... , mk |
) |
Recall from the Binomial Theorem (Thm 11.3) that the binomial coefficients are the coefficients in the expansion of (x1 + x2)n. In the same way the multinomial coefficients are the coefficients in the expansion of (x1 + x2 + ... + xk)n. This is the subject of the Multinomial Theorem 12.3.3. Recommended exercises are Exercises 12.3.1, 12.3.2, 12.3.5.
Example The two partitions P1={{a},{b},{c,d}} and P2={{a,b},{c},{d}} of the set X={a,b,c,d} both correspond to the partition of the integer 4 into 3 parts given by 4=2+1+1.
Biggs introduces partitions of integers in Sections 12.4, where he also introduces a shorthand notation for writing the partitions of an integer. All exercises in section 12.4 are very informative, so do Exercises 12.4.1, 12.4.2, 12.4.3.
Biggs continues his study of partitions in sections 26.1 and 26.2. Here he uses Ferrers diagrams to study partitions. Recommended exercises are Exercises 26.1.1, 26.1.2, 26.2.1, 26.2.2.
In Section 12.5 Biggs returns to the study of permutations of an n-set. Before you start the reading of these sections, it is a good idea to go back to section 10.6 an revise how to define the set of permutations Sn and how to find the disjoint cycle notation for a permutation.
Section 12.5 starts by classifying the permutations in Sn according to which type of disjoint cycle notation they have. Using the theory about partitions, we have just developed in sections 12.1-12.4, it is then easy to count the number of permutations of each type. Biggs does this at the bottom of p. 134.
Two permutations
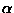 and
and
 with the same disjoint cycle decomposition are conjugate.
This means that there exists a permutation
with the same disjoint cycle decomposition are conjugate.
This means that there exists a permutation
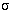
 Sn such that
Sn such that
 =
= 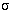
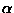
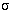 -1.
-1. 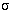 from
the two permutations
from
the two permutations 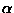 and
and
 . This is done in Theorem 12.5. The proof is easier to understand if you
choose two specific permutations e.g. (123)(45) and (543)(21) in S5 and follow the proof
through by computing the permutation
. This is done in Theorem 12.5. The proof is easier to understand if you
choose two specific permutations e.g. (123)(45) and (543)(21) in S5 and follow the proof
through by computing the permutation
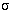 for those two.
for those two.
Good exercises from this section are Exercises 12.5.1, 12.5.2, 12.5.3.
In Section 12.6 Biggs shows that the permuatations in Sn can be partitioned into two classes each of size n!/2 in a natural way.
A transposition on an n-set X is a permutation which swaps two elements and leaves the remaining n-2 fixed. Its disjoint cycle decomposition thus consists of one 2-cycle and n-2 1-cycles. On p. 137 Biggs shows how any r-cycle can be written as a composition of transpositions. It is important to note that this can be done in many different ways and that the number of transpositions needed to express a given r-cycle may vary between the compositions for the r-cycle. However, if an r-cycle can be expressed as a composition of an odd number of transpositions then it cannot be written as a composite of an even number of transpositions and vice versa. This is the subject of Theorem 12.6.1, and this gives rise to the classification of permutations into odd permutations and even permutations.
Finally, in Theorem 12.6.2 Biggs sets up a one-to-one correspondence between the even and odd permutations of Sn, thus proving there are equally many permutations of each kind.
Good exercises from this section are Exercises 12.6.1, 12.6.2, 12.6.3, 12.6.4