
MAAB16 Discrete Mathematics B
Unit 6: More Graph Theory
Unit 6: More Graph Theory
 |
Unit 6: More Graph Theory |
In this unit we shall study edge-colourings of graphs and how they can be used to extend Latin Rectangles to become Latin Squares. After this we study bipartite graphs and in particular matchings in bipartite graphs. Matchings can be used to solve problems like finding and optimal assignment of tasks to a work force and are thus very useful for an array of practical problems. We introduce and prove an algorithms for creating a complete matching in a bipartite graph, if it exists. If a complete matching does not exist, our algorithm gives a maximum size matching.
Section 17.1 starts by defining what is meant by a relation between two sets. Basically
it is a subset of X Y. Note that a function
f: X
Y. Note that a function
f: X Y is a relation between X and Y. However, not all relations
between X and Y are functions.
Y is a relation between X and Y. However, not all relations
between X and Y are functions.
Relations between sets X and Y can be represented by bipartite graphs on the vertex set
X Y where an edge between x
Y where an edge between x  X and y
X and y  Y
means x is related to y.
Y
means x is related to y.
Example
A relation between X={1,2,3} and Y={a,b,c} which is not a function
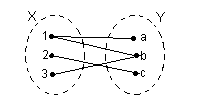
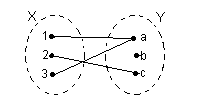
Because we are interested in relations between two sets, we study bipartite graphs.
The first thing to notice is that all edges in a bipartite graph on vertex set
X Y go between X and Y and so the sum of degrees of vertices in each
part is the number of edges in the graph. This is the content of Theorem 17.1.
Y go between X and Y and so the sum of degrees of vertices in each
part is the number of edges in the graph. This is the content of Theorem 17.1.
The section ends with an example about regular bipartite graphs. This example is important. Read it carefully! Then verify it on the following example.
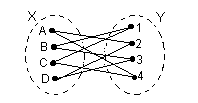
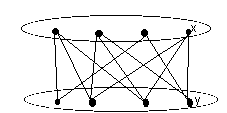
Example Here X is a set of 4 people {A,B,C,D} and Y is a set of 4 jobs {1,2,3,4} where each person is qualified to do precisely 2 jobs and each job can be done by precisely 2 people.
Recommended revision exercises are Exercises 17.1.1, 17.1.2, 17.1.3.
Sections 17.2 and 17.3 are about edge colourings of graphs. An m-edge colouring of a graph is a colouring of the edges of the graph with m colours in such a way that no two edges which meet at a vertex have the same colour. As with vertex colourings, we are interested in the smallest number of colours needed in order to colour a graph. This is what was called the chromatic index of the graph on Discrete Maths A (MAAA25).
All the edges meeting at a vertex in the graph must have separate colours, so if the maximum degree of the graph is K, then we need at least k colours to edge-colour the graph.
Example
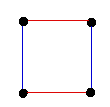
To edge-colour the cycle graph C4 we need at least two colours as its maximum degree
is 2. In this case two colours actually suffice. Here is a 2-colouring of the edges of C4
In general if G is a graph with maximum degree K, K colours is not sufficient in order to edge-colour the graph. The simplest examples that show this are the odd-length cycle graphs. You need three colours to edge-colour an odd cycle:
Example
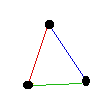
To edge-colour the cycle graph C3 we need at least two colours as its maximum degree
is 2. In this case two colours are not enough though. You need 3 colours in order to edge-colour
C3:
However, when the graph is bipartite and of maximum degree K, then K colours suffice. This is the content of Theorem 17.2.
The proof of theorem 17.2 relies heavily on the graph being bipartite. Otherwise it is an induction on the number of edges in the graph. The induction step creates a colouring of a graph G on m+1 edges with maximum degree K like e.g.
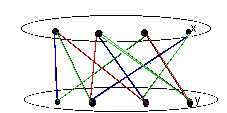
 K-1 in the graph G-{xy}, so at both these
a maximum of K-1 colours are used. If the same colour is missing at both vertices then we can just
colour xy in that colour and we are done. Otherwise we have two different colours missing,
red and blue say like in our example. The idea is now to change the colouring in such a way that
the same colour is missing at x and y.
We do that by creating a maximum alternating path of red and blue edges
starting at x (if x has a blue
edge missing and y a red one).
K-1 in the graph G-{xy}, so at both these
a maximum of K-1 colours are used. If the same colour is missing at both vertices then we can just
colour xy in that colour and we are done. Otherwise we have two different colours missing,
red and blue say like in our example. The idea is now to change the colouring in such a way that
the same colour is missing at x and y.
We do that by creating a maximum alternating path of red and blue edges
starting at x (if x has a blue
edge missing and y a red one).
Now do Exercise 17.2.4.
Section 17.3 starts by explaining that an n-colouring of the edges of the complete bipartite graph.
Kn,n on vertex set X  Y corresponds to a Latin Square of
order n. There are three ways in which you can interprete this. Biggs uses two of them:
Y corresponds to a Latin Square of
order n. There are three ways in which you can interprete this. Biggs uses two of them:
 X, y
X, y  Y,the colour of xy).
Y,the colour of xy).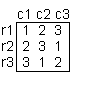
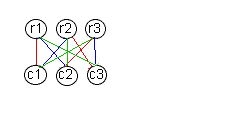
 X, y
X, y  Y,the colour of xy).
Y,the colour of xy).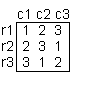

 n Latin rectangle can be
completed to a Latin Square by creating a colouring of the corresponding Kn,n and reversing the above
procedure. In Theorem 17.3.2 he gives a necessary and sufficient condition for an
m
n Latin rectangle can be
completed to a Latin Square by creating a colouring of the corresponding Kn,n and reversing the above
procedure. In Theorem 17.3.2 he gives a necessary and sufficient condition for an
m p Latin rectangle to be completed to a n
p Latin rectangle to be completed to a n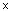 n Latin Square.
Solve also
Exercise 17.3.1 before going on to the next chapter.
n Latin Square.
Solve also
Exercise 17.3.1 before going on to the next chapter.
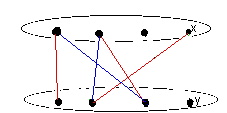
Sections 17.4 and 17.5 are about matchings. A matching is a set of edges in a (bipartite) graph on vertex
set X Y such that none of them have
a vertex in common with any of the others. The size of a matching is the number of edges in it.
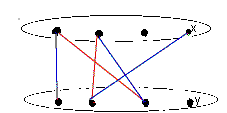
E.g. M={A2,B3,C4} is a matching (of size |M|=3) in the graph
Y such that none of them have
a vertex in common with any of the others. The size of a matching is the number of edges in it.
E.g. M={A2,B3,C4} is a matching (of size |M|=3) in the graph

 X is not matched.
X is not matched.
Not every bipartite graph has a complete matching. A necessary condition is that every set of n vertices in X has at least n neighbours in Y, as by the pigeonhole principle there is no way of matching n vertices to n-1 or less vertices without 'repeating' a vertex. It is a remarkable fact that this necessary condition is also sufficient, i.e. that if every set of n vertices in X has at least n neighbours in Y for n=1,2,3,...,|X|, then a complete matching exists. The condition is known as Hall's condition for the existing of a complete matching. Biggs proves in Theorem 17.4 that the complete matching exists provided that Hall's condition is satisfied.
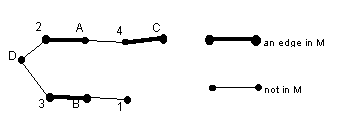
Example
We checked at the end of our treatment of section 17.1 that Hall's condition holds in the graph

The way to find the complete matching is by
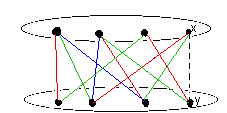
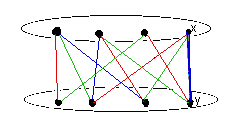
Biggs then goes on to extend the algorithm we used to find a complete matching above to find a maximum matching in any bipartite graph. The basis of the proof that the algorithm works is Theorem 17.5.2 showing that if M is a non-maximal matching in a bipartite graph G, then G contains at least one of the M-alternating paths rooted at an unmatched vertex and ending in an unmatched vertex which can be used to create a matching M1 with one more edge. Hence we can just start at any matching and augment it by a number of edges, one at a time, until no augmenting M-alternating path can be found. We then know we have a maximum matching.
Example
Let us find a maximum matching in the bipartite graph G:
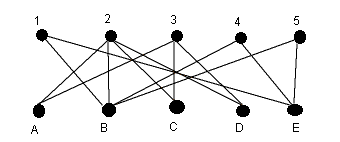
First augmentation attempt
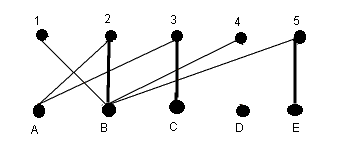
Second augmentation attempt
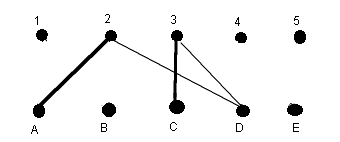
Solve also Exercise 17.5.1.