Logik II
Referenser
[EG] avsnitt 7.4 (ej 7.4.5)
samt nedanstående text.
Nyckelord
Booleske algebror. Booleske funktioner. Grindar för 'och', 'eller' och 'icke'. Logiska kretsar.
Inledning
Information kan lagras som 1:or och 0:or. En dator kan hjälpa till med omstrukturering av informationen genom att beräkna booleske funktioner m.h.a. logiska kretsar. Det är sådana beräkningar som utförs av din dators CPU.
1. Boolesk algebra
Börja nu läsa delavsnitt 7.4.1 och 7.4.2 i [EG].
En (två-värd) Boolesk algebra är en mängd {0,1} som har de tre
operatorerna +, och ', som uppfyllar
räknereglerna i tabell 7.4 sidan 211 i [EG]. I avsnitt 7.4.2 visas hur den satslogik vi
införde i block 10 kan tolkas som en Boolesk algebra. Innan du
fortsätter läsningen av avsnitt 7.4, lös då uppgift
7.53 i [EG], så du är säker på att du har förstått den nya
notationen.
och ', som uppfyllar
räknereglerna i tabell 7.4 sidan 211 i [EG]. I avsnitt 7.4.2 visas hur den satslogik vi
införde i block 10 kan tolkas som en Boolesk algebra. Innan du
fortsätter läsningen av avsnitt 7.4, lös då uppgift
7.53 i [EG], så du är säker på att du har förstått den nya
notationen.
2. Booleske funktioner
Läs nu delavsnitt 7.4.3 i [EG] om Booleska funktioner. Dessa funker precis som de sanningstabeller vi introducerade i block 10, men användar den nya notationen vi just lärt oss.
En bit är en variabel som antingen är 0 eller 1. En boolesk funktion av n variabler har som indata bitar x1, x2, ..., xn och som utdata en bit som kan beskrivas med ett booleskt uttryck i bitarna x1, x2, ..., xn. I exempel 7.15 visas ett exempel på en boolesk funktion med tre bitar som indata.
Exempel
Antag att vi vill med OCH, ELLER och ICKE operationer beskriva en boolesk funktion f med tre bitar x1, x2, x3 som indata och med utdata som anges av följande värdetabell.|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ett logiskt uttryck som beskriver utdata med indata är ett steg mot problemets lösning. I kolumnen för utdata återfinns tre ettor. Det logiska uttrycket x1
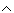 x2
x2
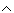 x3 antar
värdet 1 för
den första raden i värdetabellen och 0 annars.
Det logiska uttrycket
x1
x3 antar
värdet 1 för
den första raden i värdetabellen och 0 annars.
Det logiska uttrycket
x1 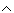 x2
x2
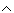
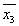 antar värdet 1 för
den andra raden i värdetabellen och 0 annars.
Det logiska uttrycket
antar värdet 1 för
den andra raden i värdetabellen och 0 annars.
Det logiska uttrycket
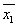
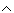
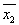
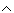 x3 antar värdet 1 för
den sjunde raden i värdetabellen och 0 annars.
Sätter vi ihop dessa delar med eller operatorn
x3 antar värdet 1 för
den sjunde raden i värdetabellen och 0 annars.
Sätter vi ihop dessa delar med eller operatorn 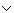 till
(x1
till
(x1 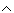 x2
x2 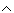 x3)
x3)
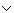 (x1
(x1 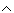 x2
x2 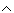
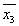 )
)
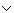 (
(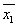
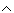
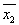
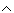 x3) får vi
ett logiskt
uttryck som beskriver utdata med indata, och om vi skrivar om detta uttryck till
den nya notationen får vi
x3) får vi
ett logiskt
uttryck som beskriver utdata med indata, och om vi skrivar om detta uttryck till
den nya notationen får vi
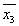 +
+
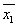
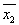 x3.
x3.

I exemplet ovan såg vi att den booleska funktionen
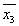 +
+
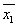
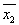 x3
x3 kunde beskriva en utdata-tabell som var mycket lik en sanningstabell för logiska uttryck. Den speciella form den booleska funktionen är angiven med kallas disjunktiv normalform.
En minterm i symbolerna
x1, x2,..., xn är ett logiskt uttryck
på formen
y1 y2
...
yn där varje
yi är antingen
xi eller 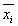 .
En boolesk
funktion med n variabler som indata är beskriven på
disjunktiv normalform
om det booleska uttrycket består av mintermer med n variabler
sammansatta
med + operatorer.
.
En boolesk
funktion med n variabler som indata är beskriven på
disjunktiv normalform
om det booleska uttrycket består av mintermer med n variabler
sammansatta
med + operatorer.
I delavsnitt 7.4.3 visas ett par vägar som kan följas för att skriva om ett booleskt uttryck motsvarande ett logiskt uttryck för att komma till dess disjunktiva normalform. Denna del av avsnittet är viktig men delan om maxtermer och omskrivning till konjuntiva normalformer kan läsas kursivt.
3. Grindar och logiska kretsar
En logisk krets med bitar x1, x2,..., xn och y1, y2,..., ym beskriver en Boolesk funktion med bitarna med namnen y som utdata och bitarna med namnen x som indata.
En logisk krets byggs med grindar som kan ändra bitars värden
efter
olika regler. En OCH-grind är i sig själv en logisk
krets vilken
har som indata två bitar x1 och x2 och
utdata en bit y.
OCH-grindens utdata definieras som logiska operationen "och" i block 10.
Dvs. OCH-grinden kan definieras enligt
sanningstabellen för x1 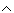 x2:
x2:
|
|
|
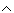 x2
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Läsa nu delavsnitt 7.4.4 i [EG]. På sidan 215 definieras OCH-grinden, ELLER-grinden och ICKE-grinden (även kallad en inverterare). Där återfinns även bilder på hur de ska ritas i ett kopplingschema.
På sidan 216 visas hur man kan koppla ihop grindar till en större kombinatorisk krets. Notera hur man börjar inifrån det booleska uttrycket och arbetar sig utåt under konstruktionen av kretsen.
Vid tillverkning av kretsar är det bra om bara ett fåtal grindar, och dessa gärna av samma sort, behäver användas. En godtycklig logisk krets kan konstrueras om vi bara har tillräckligt många OCH, ELLER och ICKE grindar. Med denna egenskap sägs grindarna OCH, ELLER och ICKE vara funktionellt fullständiga. Vi kan fråga oss om någon äkta delmängd till {OCH,ELLER,ICKE} också är funktionellt fullständig. En speciell grind, NAND-grinden, visar sig vara funktionellt fullständig i sig själv. Detta diskuteras i delavsnitt 7.4.4.4 i [EG].
4. Övningsuppgifter
Övningsuppgifter från [EG] kapitel 7:
7.53, 7.54, 7.56, 7.57, 7.58;
7.83, 7.84,
7.87 (ej konjunktiv normalform), 7.88 (ej konjunktiv normalform),
7.89.
Week Exercise 11
Lös uppgift 7.98 i [EG] (sida 229). Motivera alla steg i dina svar!This is the 2nd Edition of the study guide for Block 11 of Discrete Mathematics for the Vocational
Study Programme in Information Technology, written by
Pia Heidtmann in 2006.
The study guide may be printed for personal use by
anybody with an interest.
This study guide and any parts of it and any previous and future versions of it must not
be copied or disseminated in any printed or electronic form
or stored on any publicly accessible website other than
http://www.tfm.miun.se/~piahei/dmy/res/
without permission from the author.
The author welcomes comments and corrections via email.
All contributions incorporated in updates of the manuscript will be acknowledged.
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
