Relationer och funktioner

Referenser

[D] avsnitt 1.8;
[EG] avsnitt 8.1, 8.2 (ej 8.2.3) samt
nedanstående text

Nyckelord

Relationer på en mängd, relationer mellan två mängder. Egenskaper hos relationer på en mängd: reflexivitet, symmetri, anti-symmetri, transitivitet. Ekvivalensrelationer och partialordninger. Totalordninger.
Funktioner. Injektive, surjektive, bijektive funktioner.

Inledning

I detta block skall vi studera relationer på mängder, och vi skall se hur några speciella relationer kan användas för att dela upp, partitionera, en mängd i delmängder, så att man kan urskilja några strukturella egenskaper hos mängden. Slutligen skall vi se på funktioner, ett område som du känner igen från gymnasietiden.
 

1. Relationer

Vi skall nu studera relationer på mängder. I princip kan man säga att en relation på en mängd X, är ett sätt att beskriva ett samband mellan elementen i X.
 

Exempel
Låt M vara mängden av alla personer i världen, då kan vi definiera relationen R på M genom att låta
person x vara relaterad till person y om och endast om x är född samma månad som y.

Om x är relaterad till y under relationen R skriver vi

xRy

Exempel
Låt M vara mängden av alla personer i världen, då kan vi definiera andra relationer på M. T.ex.

• xR₁y om och endast om x har samma kön som y.
• xR₂y om och endast om  x är yngre än y.
• xR₃y om och endast om x är syster till y.
• xR₄y om och endast om x känner  y.
• xR₅y om och endast om x förstår det språk som y talar.

 

Exempel
Låt 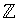 vara mängden av heltalen, då är följande relationer på   :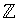

• xR₁y om och endast om x < y.
• xR₂y om och endast om y är en faktor i x.
• xR₃y om och endast om x 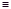  y (mod  5).

Mer formellt, definierar vi en relation R på en mängd S att vara en delmängd till den kartesiska produkten X × X.
Det ordnade paret (x,y)R om och endast om xRy.

Exempel
Betrakta relationen R på S={1,2,3} definierad genom xRy om och endast om x  y .

Då har vi att 1R1, 2R1, 3R1, 2R2, 3R2 och 3R3 eftersom 1 1, 2 1, 3 1, 2 2, 3 2 och 3 3.

R kan också beskrivas som en delmängd av S × S, nämligen

R={(1,1), (2,1), (3,1), (2,2), (3,2), (3,3)}.

Man kan ochså rita en bild som beskriver relationen:

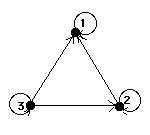
Detta kallas för digrafen för relationen på S={1,2,3}. I [EG] betecknas digrafen för en relation också relationsgrafen.

Nu skall du läsa [EG] avsnitt 8.1. Börja med introduktionen s. 232 och delavsnitt 8.1.1. En relations  digraf  beskrivas på s. 233-234.

Delavsnitt 8.1.2 läsas senare och delavsnitt 8.1.3 läsas kursivt.

Vi kan klassificera relationer utifrån egenskaper. En relation R på X sägs vara

• reflexiv om för alla x X det gäller att (x,x) R;


• symmetrisk om för alla x, y X det gäller att om (x,y) R så är även (y,x) R;


• anti-symmetrisk om för alla x, y X det gäller att om (x,y) R och x 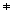y så är (y,x) 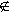R;


• transitiv om för alla x, y, z X det gäller att om (x,y) R och (y,z) R så är även (x,z) R.

Var och en av dessa egenskaper kan kontrolleras genom att studera relationens digraf:
Om relationen är reflexiv, finns det en loop vid varje hörn i digrafen.
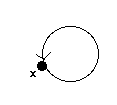
Notera att relationen  på S={1,2,3} är reflexiv eftersom det finns en loop vid alla hörn 1, 2 and 3 i digrafen vi ritade ovan.

Om relationen är symmetrisk, så gäller att om det finns en pil från hörn x till hörn y i relationens digraf, så skall det också finnas en pil från y tillbaka till x.

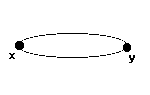
Notera att relationen   på S={1,2,3} inte är symmetrisk, eftersom det finns en pil från hörn 2 till hörn 1 i relationens digraf, men ingen pil från hörn 1 till hörn 2.

Om relationen är transitiv, gäller att om det går en pil mellan x och y i relationens digraf och en pil mellan y och z, så skall det finnas en pil mellan x och z.

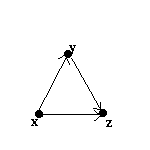
Notera därmed att relationen på S={1,2,3} är transitiv.

Om relationen är anti-symmetrisk, gäller att om det finns  en pil mellan x och y i relationens digraf, så skall det inte finnas  någon pil från y tillbaka till x, såvida inte x=y. Notera   därför att relationen på  S={1,2,3} från ovan är antisymmetrisk. 

Observera att för att kontrollera om någon av dessa egenskaper gäller för en relation, räcker det inte att kontrollera att egenskapen uppfylls för några speciella val av x, y och z, utan egenskapen måste gälla för alla möjliga val av x, y och z. Tag till exempel,  relationen  på S={1,2,3} från ovan, vi ser klart att det går en pil från  x=1 till y=1, så naturligtvis går samma pil tillbaka från y=1 till x=1, men relationen är inte symmetrisk för det, eftersom vi upptäckte att det går en pil från hörn  x=2 till hörn y=1, men det finns ingen pil från hörn y=1 tillbaka till hörn x=2.

Läs nu delavsnitt 8.1.4 i [EG].

Relationer på en mängd X kan användas vid försök att ordna elementen på rad. En partialordning på en mängd X är en relation på X som är reflexiv, antisymmetrisk och transitiv. Relationen  på S={1,2,3} ovan är därför en partialordning. Av namnet finns en antydan om att man bara delvis (partiellt) lyckas ordna elementen på en rad med en partialordning och detta kan vara fallet. Två element i X behöver inte vara "jämförbara" med en partialordning.

En totalordning (också kallat en fullständig ordning) på en mängd X är  en partialordning i vilken varje par av element i X är jämförbara.  Relationen on S={1,2,3} ovan är  därför även en fullständig ordning. Ett tredje namn  på en fullständig ordning som också används är  linjär ordning vilket belyser att elementen ordnas på linje  med denna relation. Läs nu delavsnitt 8.1.5 i [EG]. En  relation R på en mängd X som är reflexiv, symmetrisk och  transitiv kallas en  ekvivalensrelation. 

Exempel
Relationen R på 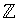 definierad som (x,y)R om x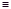 y (mod n) är en ekvivalensrelation (Kontrollera detta! Dvs. kontrollera att R är reflexiv, symmetrisk och transitiv).

Tidigare såg vi att tal som är kongruenta bildar kongruensklasser  och att mängden av kongruensklasser är en partition av 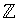.  Mer allmänt bildar element i X som är ekvivalenta (d.v.s. de  element som är relaterade med ekvivalensrelationen R) ekvivalensklasser   och mängden av dessa ekvivalensklasser är en partition av X.

Exempel
Låt oss definiera en relation R på 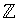 genom (x,y) R om x²=y² . Våra uppgifter är (a) att visa att R är en ekvivalensrelation och (b) att beskriva ekvivalensklasserna.

För (a): För alla heltal x så gäller att x² = x² och (x,x) R så R är reflexiv.
Antag att x och y är heltal och (x,y) R. Att paret tillhör R betyder att x² = y². Detta är detsamma som att y² = x² vilket betyder att (y,x) R. Talen x och y valdes godtyckligt med egenskapen att (x,y) R så vi kan dra slutsatsen att R är symmetrisk.
Om x, y och z är heltal sådana att x² = y² och y² = z² så innebär det att x² = z². Detta uttalande är precis det samma som att säga att relation R är transitiv.

För (b): Ekvivalensklassen med elementet n 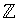är
[n]={x 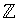| (x,n) R} = {x 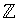| x² = n²} = {x 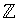| (x+n)(x-n) = 0} = {n, -n}.
Den sista likheten av det faktum att produkten (x+n)(x-n) är 0 precis då faktorn (x+n) eller (x-n) är 0. Partitionen av 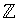 med ekvivalensklasserna till denna ekvivalensrelation R blir alltså {{0}, {-1,1}, {-2,2}, {-3,3}, {-4,4}, ...}.

2. Funktioner

Fram till nu har vi bara studerat relationer på én mängd. Det  är också möjligt att definiera en relation som beskriver  sammanhang mellan element som tillhör två olika mängder  X och Y. Minns att en relation på en mängd formellt kan definieras  som en delmängd till den kartesiska produkten X × X. På  samma sätt kommer en relation från en mängd X till en mängd  Y att vara en delmängd till den kartesiska produkten X × Y.  Läs nu avsnitt 8.1.2 i [EG], som beskriver relationer  mellan två mängder istället för relationer på  én mängd. 

Läs nu avsnitt 8.2 i [EG]. 
En funktion f från X till Y är en relation från X till Y med egenskaperna att

1. definitionsmängden (engelska: domain) är hela X,
2. om (x,y) f och (x,z) f så är y = z.

Y är funktionens målmängd (också kallat bildmängd) (engelska: codomain). Egenskaperna tillåter oss att prata om värdet y Y av funktionen i x X. Det vill säga att varje x X återfinns som förstakoordinat i precis ett ordnat par i relationen. Vanligt är att skriva y = f(x) istället för (x,y) f för att ytterliggare illustrera att funktionen f har värdet y i x. Man kan tänka på en funktion f från X till Y som en maskin som har "x-värden" som indata och  "y-värden" som utdata. För varje indatavärde kastar maskinen ut precis ett utdatavärde. Mängden av alla utdatavärden kallas för funktionens värdemängd (engelska: range).

Exempel
Med X={1, 2, 3} och Y={a, b, c} är

f = {(1,a), (2,b), (3,b)}
en funktion från definitionsmängden X till bildmängden Y, f:s värdemängd är {a, b}.

Däremot är inte g = {(1,a), (2,b), (3,b), (3,c)} en funktion från X till Y. Relationen g har som definitionsmängd hela X men andra egenskapen ovan är inte uppfylld eftersom båda (3,b) g och (3,c) g.

Exempel
Regeln att till varje reellt tal multiplicera detta med 5 och sedan addera 2 kan ses som en funktion f från 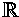 till 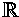 definierad med y = f(x) = 5x + 2. Istället för att ge sig på att rita denna relations digraf kan man som illustration ange denna funktions graf i det kartesiska koordinatsystemet av 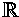 och 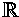 . Denna uppgift skulle också kunna formuleras som "rita funktionen y = 5x+2 i xy-planet" där namnet på funktionen har uteslutits och där det är underförstått att xy-planet är det kartesiska koordinatplanet av 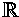 och  .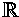

Begreppen injektiv och surjektiv

Att räkna de femton kakorna på ett brödfat är detsamma  som att definiera en funktion f från mängden {1, 2, 3,...,15} till mängden {x | x är en kaka på brödfatet} som är injektiv (varje kaka räknas bara en gång) och surjektiv (varje kaka räknas). Även om  detta exempel illustrerar betydelsen av orden injektiv och surjektiv kan  detta exempel kanske missförstås. Definitionen av begreppen "ett till ett" eller injektiv och "på" eller surjektiv för en funktion hittar man på  sidorna 249 - 250. En funktion som är både  injektiv och surjektiv sägs vara bijektiv.

3. Övningsuppgifter

Övningsuppgifter från [D] avsnitt 1.8:

1.49, 1.51, 1.52.

Övningsuppgifter från [EG] kapitel 8:

8.1, 8.2, 8.3, 8.4, 8.5;
8.10,, 8.12, 8.15, 8.16, 8.17, 8.18;
8.19, 8.20, 8.21, 8.22, 8.23;
8.25, 8.26, 8.28;
8.6, 8.30, 8.31, 8.32;
8.34, 8.36, 8.37, 8.40, 8.45, 8.46, 8.47, 8.48;
8.63, 8.64, 8.65, 8.66;
8.69, 8.70, 8.72

Week Exercise 12

Please click here to download the week exercise in pdf-format.