Tal och aritmetik I

Referenser

[EG]   avsnitt 3.1, 3.2;
[D]      avsnitt 3.1, 3.2;
[EG]   avsnitt 3.3 (t.o.m. delavsnitt 3.3.3);
och nedanstående text.

Nyckelord

Decimala talsystemet, det binära och det hexadecimala talsystemen, divisionsalgoritmen för division av heltal med kvot och rest. Delare, primtal och primtalsfaktorisering.

Inledning

I detta block skall vi se på, hur vårt talsystem är uppbyggt, och vi introducerar det binära och det hexadecimala talsystemen, som båda används inom t.ex. datalogi. Vi skall också lära oss att räkna i dessa två nya talsystem, och vi kommer att utveckla algoritmer för att konvertera tal från ett talsystem till ett annat. Därnäst skall vi gå igenom delare och primtal och vi skall lära oss rita delargrafen för ett heltal.

1. Divisionssatsen

Läs nu avsnitt 3.1 i [EG], det handlar om division med kvot och rest.

Grundläggandet för att konvertera ett tal i 10-talssystemet till ett tal i talsystemet med bas N är följande mycket viktiga egenskap vid division med heltal, som är sats 3.1 i [EG], den går under namnet Divisionssatsen :

Sats 3.1 i [EG] (Divisionssatsen).
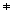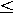Givet ett godtyckligt heltal a och ett heltal N, där N 0, så existerar det entydigt bestämda heltal k och r (som kallas kvoten och resten) sådana att a=kN+r och 0 r 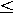|N|-1.

Du känner säkert redan till en del av detta resultat, det säger, att när man dividerar ett heltal med ett positivt heltal N, så kan man arrangera det så att man alltid får en rest bland talen 0,1, ... , N-1. [EG] kallar denna resten för den principala resten.

Exempel
Tag till exempel a=23 och N=3, då får man kvoten 7 och resten 2, eftersom 23=7 3 +2.

Om man delar a=25 med N=3, så får man kvoten 8 och (principala) resten 1, eftersom 25=(8) 3 +1.
Om man delar a=-25 med N=3, så får man kvoten -9 och (principala) resten 2, eftersom -25=(-9) 3 +2.
Om man delar a=25 med N=-3, så får man kvoten -8 och (principala) resten 1, eftersom 25=(-8) (-3) +1.
Om man delar a=-25 med N=-3, så får man kvoten 9 och (principala) resten 2, eftersom -25=(9) (-3) +2.

Vi skall inte bevisa Divisionssatsen på denna kurs, men du skall känna till resultatet och du skall kunna formulera satsen. Du skall också kunna hitta kvoten och (principala) resten då a delas med N med hjälp av divisionsalgoritmen som [EG] demonstrerar i Metod 3.1 på sidan 37.

Övning B3.1

Hitta den enligt Divisionssatsen entydigt bestämda kvoten och (principala) resten, när a delas med N, där

• a=12 och N=7;
  


• a=-12 och N=7;
  


• a=22 och N=3;
  


• a=-22 och N=3;
  


• a=-22 och N=-3;
  


• a=22 och N=-3.
  

2. Talsystem

Vi skall nu lära oss om talssystem och talbaser, men innan vi läsar avsnitt 3.2 i [EG] är det en bra idé att läsa avsnitt 3.1 och 3.2 i [D] för att repetera aritmetik med rötter och potenser.

Övning B3.2
Lös uppgift 3.1 - 3.4, 3.6 - 3.10 i [D].

Läs nu avsnitt 3.2 i [EG] om baser för systemet av heltal och hur man konverterar från en bas till en annan.

2. Primtal och delare

Läs nu avsnitt 3.3 i [EG] t.o.m. delavsnitt 3.3.3:

Delare

Delavsnitt 3.3.1 handlar om delare. Ett heltal b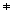 0 sägs  vara en delare (också kallad en faktor) till heltalet a, om det finns ett heltal k, som vi kallar kvoten, sådan att a=bk. Med andra ord är b en delare till a om man får (principala) resten 0 då man delar a med b. Med matematiska symboler skriver vi detta på formen b | a och vi läser det som 'b delar a'.  Om ett heltal b inte är en delare till a, indikerar vi detta genom att sätta ett streck över '|'-symbolen, dvs. vi skriver b a och läser detta som 'b delar inte  a'. 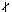Observera att det lodräta strecket i denna notation inte är ett bråkstreck, 'b | a' skall inte förväxlas med 'b/a'.

Vi difinierar också ett specialfall: 0 sägs vara en en delare till 0, men 0 är inte delare till något annat heltal.

Du skall kunna följande fundamentala resultat för delare:

Sats B3.1.
Låt m, n och c vara heltal sådana att c | m och c | n.
Då gäller att c | (m+n) och c | (m-n).

Bevis.
Eftersom m och n bägge har c som delare kan vi hitta två kvoter q₁ och q₂, bägge heltal, sådana att
m=cq₁ och n=cq₂. Därför är

m+n=cq₁+cq₂= c(q₁+q₂), så c är alltså en faktor i m+n, dvs. c | (m+n).

På samma sätt har vi att m-n=cq₁-cq₂ =c(q₁-q₂), så c är också en faktor i m-n, dvs. c | (m-n).

Exempel
2 delar 4 och 2 delar 6, så 2 delar 10 och -2. 
 

Sats B3.2.
Låt m, n och c vara heltal, som uppfyller att c | m och m | n.
Då har vi att c | n.

Bevis.
Eftersom m  har c som delare kan vi hitta en heltalskvot q₁ sådan att
m=cq₁. På samma sätt har vi att n har m som delare, så det existerar också ett heltal q₂ sådant att n=mq₂.
Vi har därför att n=mq₂ =(cq₁)(q₂ )=c(q₁q₂), och c är därför också en faktor i n, dvs. c | n. 

Exempel
2 delar 4 och 4 delar 20, så 2 delar 20.

Exempel
Om du vet att 2 inte delar heltalet k, så vet du också att 4 inte delar k.  

Primtal

Om  b | a säger vi att a är en multipel av b, och uttrycket a=bk kallas en faktorisering av a.

Talen 1 och -1 är speciella heltal, när vi talar om faktorisering, eftersom de delar alla heltal. Vi har därför ett speciellt namn för dessa två tal, de är så kallade enheter i 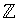. Varje heltal a har naturligtvis de två triviala faktoriseringarna

a=(a)(1) och a=(-a)(-1),

dvs. 1, -1, a,  och -a är alltid delare till heltalet a om a 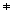0. Vi kallar ett heltal b 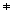0 för en äkta delare till a, om b | a och b inte är en av delarna 1, -1, a,  eller -a. I delavsnitt 3.3.2 i [EG] definieras en delmängd av de positiva heltalen som kallas för de sammansatta talen, dessa har en äkta delare. Ett primtal är ett positivt heltal, som inte är en enhet och inte har äkta delare.

Exempel

• 6 är ett sammansatt tal, eftersom 6=(2)(3) och 6 har därför 2 och 3 som äkta delare.

• 1 är inte ett sammansatt tal, eftersom de enda delarna till 1 är -1 och 1 själva.
 

• 2 är ett primtal, eftersom 2 inte är en enhet och de enda delarna till 2 är 1, -1, 2 och  -2, så 2 har inga äkta delare.


• 1 är inte ett primtal, eftersom det är en enhet.

Matematiker har ända sedan antiken forskat om primtal, men trots detta finns det än i dag många olösta problem omkring primtal. Ett av de största problemen var länge att hitta en snabb algoritm för att bestämma om ett givet heltal n är ett primtal eller ej. Detta problem blev dock löst 2002 av två studenter vid Indian Institute of Technology i Kanpur vid namn Kayal och Saxena, när de hittade den så kallade AKS-algoritmen tillsammans med deras handledare Agrawal. Vi skall inte lära oss AKS-algoritmen på denna kurs, men det är bra att veta att den existerar, om du skulle få användning för den i framtiden. Låt oss i stället se på några primtalstest som fungerar för små tal, där problemet inte är så stort och svårt, att det är nödvändigt med smarta algoritmer. Man kan t.ex. prova sig fram med alla möjliga delare:

Exempel
Låt oss undersöka, om 151 är ett primtal.

Vi kan självklart lösa detta problem genom att dela 151 med alla talen 2, 3, 4, 5, 6, ..., 150 och därmed kontrollera om ett av dessa delar 151; men detta kräver 149 divisioner och tar lång tid! Om vi tänker oss för, kan vi kanske hitta på en mer effektiv metod...

Vi observerar först, att 2 inte delar 151. Är det då möjligt att 4 delar 151? Eller 6? Eller 8, 10, 12, 14,..., 150?
Svaret är nej, eftersom det ur sats B3.2 följer, att om heltalet 2k delar 151, då delar 2 också 151 eftersom 2 delar 2k. På liknande sätt ses, att eftersom 3 inte delar 151, så delar ingen multipel av 3 talet 151 heller.
Slutsatsen är, att vi, på grund av sats B3.2, endast behöver kontrollera, om alla primtal mindre än 151 är delare till 151. Detta reducerar problemet en hel del, men det är fortfarande för många tal att kontrollera, så vi tänker oss för lite till...

. . . och vi inser då, att om det finns två heltal a och b, sådana att 151=ab, måste minst ett av dessa vara mindre än eller lika med 13 (Varför? Ledning: om både a och b är större än 13, hur stort är talet ab då?).

Vi kan därför nöja oss med att kontrollera om 2, 3, 5, 7, 11 och 13 delar 151, och eftersom inget av dem gör det, kan vi dra slutsatsen att 151 är ett primtal. Det krävs alltså endast 6 divisioner för att slå fast att 151 är ett primtal.

Exempel
Hur många divisioner krävs för att kontrollera om 397 är ett primtal? Svar: 8
(nämligen division med 2, 3, 5, 7, 11, 13, 17 och 19)

Metoden från föregående exempel med att kontrollera alla möjliga primtalsdelare upp till 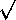n är tillräckligt bra för att kontrollera om små tal n är primtal; men om n är ett stort tal, t.ex. med 1000 siffror eller fler, så är denna metod inte tillräckligt effektiv, inte ens med hjälp av dagens snabbaste datorer. Det är ett öppet forskningsproblem, om det existerar en mycket snabb algoritm som kan faktorisera alla heltal, även mycket stora, dvs. skriva dem som en produkt av två äkta delare. Ett av nutidens mest använda krypteringssystem (ett krypteringssystem är ett system för utväxling av hemliga meddelanden), det så kallade RSA-krypteringssystem, bygger på, att faktorisering av stora tal är ett mycket svårt matematisk problem, så om du har lust, tid och goda ideer finns det här en möjlighet till att bli berömd!

Primtalsfaktorisering

Vi presenterar nu en mycket viktig egenskap hos primtal:

Sats B3.3.
Låt m och n vara heltal som båda är skilda från noll, och låt p vara ett primtal så att  p | mn, då gäller
antingen att p | m eller att p | n   (eller p delar båda).

Exempel
Låt m = 36, då finns det många olika faktoriseringar av 36 med två faktorer, t.ex.

36 = 36·1 = 18·2 = 12·3 = 9·4 = 6·6 = (-6)·(-6) = (-9)·(-4) = . . .

De enda primtal, som är delare till 36 är -2, 2, -3 och 3, och sats B3.3 säger, att varje gång vi har en faktorisering av 36  med två faktorer, så delar dessa minst en av faktorerna. Tag t.ex. p=3: i faktoriseringen 36·1 delar 3 den första faktorn, i faktoriseringen 18·2 delar 3 den första faktorn,  i faktoriseringen 12·3 delar 3 den första och också den andra faktorn, etc.

Vi skall inte bevisa sats B3.3 på denna kurs, men du skall känna till resultatet och du skall kunna formulera satsen.

Exempel
Sats B3.3 är inte sann om inte p är ett primtal. T.ex. har vi att 6 | 36 och att 36=4·9, men 6 delar varken 4 eller 9.

Nederst på sidan 43 i [EG] presenteras en av algebrans huvudsatser. Den säger att alla heltal är uppbyggda av primtal. Vi ska inte bevisa denna sats på den här kursen, men nämner, att sats B3.3 är en av hörnstenarna i beviset:

Sats 3.2 i [EG] (Aritmetikens fundamentalsats)
Varje heltal (utom noll) kan skrivas som en produkt av precis en enhet och ett ändligt antal primtal.
Det gäller ytterligare, att denna faktorisering är entydig sånär som på faktorernas ordning.
 

Exempel
Vi skriver 6 som en produkt av en enhet och primtal:

6 = (1)(2)(3),
enheten är här 1, och det är två primtalsfaktorer, nämligen 2 och 3. Att faktoriseringen  är entydig sånär som på faktorernas ordning betyder att de sex faktoriseringarna

6 = (1)(2)(3) = (1)(3)(2) = (2)(1)(3) = (2)(3)(1) = (3)(1)(2) = (3)(2)(1)
alla uppfyller satsens betingelser; men att vi inte räknar dem som fundamentalt olika.

Exempel
Vi skriver -6 som en produkt av en enhet och primtal:

-6 = (-1)(2)(3),
enheten är här -1, och det är två primtalsfaktorer, nämligen 2 och 3.

Delargrafen

I delavsnitt 3.3.3 visar [EG] hur man ritar delargrafen för ett positivt heltal. Du skall kunna rita en sådan delargraf.

4. Förslag till övningsuppgifter

Övningar i texten ovan.

Övningar från [EG] kapitel 3:

3.2, 3.3(a)-(b),
3.4, 3.5, 3.6, 3.7,
3.9, 3.11, 3.12, 3.13, 3.14,
3.16, 3.17, 3.18,
3.37.

Week Exercise 4

Uppgift 1

(a) Uttryck det binära talet  (1101010001011)₂  som
     (i) ett decimaltal;

    (ii) ett oktaltal;

   (iii) ett hexadecimaltal.
 
 

(b) Uttryck decimaltalet 18723 som

       (i) ett oktaltal;

       (ii) ett binärtal;

       (iii) ett hexadecimaltal.

 

(c) Antag att de decimala heltalan x och y är representerade i det binära talsystemet genom

                        x =  (a_n a_n-1 a_n-2 . . . a₁ a₀)₂   och;

                        y =  (a_n a_n-1 a_n-2 . . . a₁ a₀  0 0 0)₂.

     Hur är x och y relaterade till varandra som decimala tal?

Uppgift 2

Primtalsfaktorisera talen 10941 och 13243. (Visa dina uträkningar!)

Uppgift 3

Rita delargrafen för 12.