Tal och aritmetik II

Referenser

[EG]   avsnitt 3.3.4 (ej 3.3.4.1);
[EG]   avsnitt 3.3.5;
och nedanstående text.

Nyckelord

Delare, linjärkombinationer, största gemensamma delaren för två heltal, Euklides algoritm, lösning av linjära diofantiska ekvationer.

Inledning

I detta block skall vi se närmare på några fundamentala egenskaper hos heltal. Vi skall se, att det finns ett mycket viktigt samband mellan den största gemensamma delaren av två heltal och linjärkombinationerna av dessa två heltal. Vi skall också gå igenom Euklides algoritm, som är en metod för att hitta den största gemensamma delaren av två heltal. Till sist i blocket skall vi lära oss lösa linjära diofantiska ekvationer.

1. Linjärkombinationer

Läs nu första sidan av delavsnitt 3.3.4 i [EG], det handlar om linjärkombinationer.

Om m och n är heltal, kallar vi varje heltal på formen sm+tn, där s och t också är heltal, för en linjärkombination av m och n.

Exempel
Om t. ex. m=3 och n=7, så är alla följande tal linjärkombinationer av m och n:

 3 :    låt s=1 och t=0, då är 3= (1)(3)+(0)(7);
 7 :    låt s=0 och t=1, då är 7= (0)(3)+(1)(7);
 0 :    låt s=0 och t=0, då är 0= (0)(3)+(0)(7);
-7 :    låt s=0 och t=-1, då är -7= (0)(3)+(-1)(7);
40:    låt s=-3 och t=7, då är 40= (-3)(3)+(7)(7).

Uppgift B4.1
Prova nu att skriva vart och ett av talen i ovanstående exempel som en linjärkombination av 3 och 7, där värdena av s och t är andra än de som givits i exemplet. Svar!

[EG] bevisar en sats nederst på sidan, som utvidgar sats B3.1 från block 4 till att gälla inte bara för m+n och m-n utan för alla linjärkombinationer av m och n:

Sats 3.4 i [EG].
Låt m och n vara heltal och låt d vara ett heltal, som delar både m och n ( ett sådant tal kallas en gemensam delare till m och n), dvs. d | m och d | n. Då gäller för alla heltal s och t, att d | (sm+tn).

Uppgift B4.2
(a) Finn alla heltal mellan -12 och 12 som är linjärkombinationer av 3 och 7;

(b) Finn alla heltal mellan -12 och 12 som är linjärkombinationer av 4 och 6;

(c) Finn alla heltal mellan -12 och 12 som är linjärkombinationer av 6 och 9.

Svar!

Du fann förhoppningsvis i uppgift B4.2(b) att 2 är delare i alla linjärkombinationer av 4 och 6, och i B4.2(c) att 3 är delare i alla linjärkombinationer av 6 och 9. Kan du se ett samband mellan 2 och talen 4 och 6? Är det kanske ett liknande samband mellan 3 och talen 6 och 9? Vi ska svara på denna fråga lite senare.

2. Största gemensamma delare

Läs nu sidan 47 i delavsnitt 3.3.4 i [EG] till Metod 3.4, det handlar om största gemensamma delaren för två heltal.

Definition
Låt m och n vara två heltal, som inte båda är noll, och låt s vara ett positivt heltal som uppfyller följande två krav:

(i) s | m och s | n, och

(ii) om d | m och d | n så gäller att d | s,

då kallas s för den största gemensamma delaren (förkortas sgd) till m och n. Vi skriver detta som sgd(m,n). På engelska kallas största gemensamma delaren för greatest common divisor, och man använder därför förkortningen gcd och skriver alltså gcd(m,n).

Låt oss se lite närmare på definitionen av sgd:

För det första är sgd(m,n) alltid ett positivt heltal. Därutöver säger det första kravet, att sgd(m,n) är en gemensam delare till m och n, dvs. sgd(m,n) delar både m och n. Det andra kravet är lite mera invecklat. Det säger, att varje delare till både m och n också är en delare till sgd(m,n). Detta medför att sgd(m,n) är den numeriskt största gemensamma faktor i m och n (varför?). För små tal, är det mycket lätt att hitta den största gemensamma delaren:

Exempel
sgd(3,7)=1;
sgd(4,6)=2;
sgd(6,9)=3;
sgd(-4,6)=2 (varför är den inte -2?);
sgd(-4,-6)=2  (varför är den inte -2?);

Huvudresultatet, som du skall känna till för största gemensamma delare är följande viktiga sats, som vi skall använda senare, men som vi inte skall bevisa i denna kurs.

Sats B4.1
Låt m och n vara två heltal som inte båda är noll, då existerar deras största gemensamma delare sgd(m,n), och det existerar dessutom heltal s och t så att sgd(m,n) =sm+tn.  

Satsen säger, att  den största gemensamma delaren till m och n existerar och kan skrivas som en linjärkombination av m och n. Slås detta ihop med sats 3.4 i [EG] fås följande följdsats:

Följdsats B4.2.

Låt m och n vara två heltal, som inte båda är noll och låt g= sgd(m,n). Låt vidare

L={x |  x=am+bn,  a,b  }       och       M={kg |  k }
dvs. L är mängden av linjärkombinationer av m och n, och M är mängden av multipler av sgd(m,n).
Då är L=M.

Denna följdsats är resultatet, som ligger till grund för observationen efter uppgift B4.2 (se uppgift B4.3 nedan). Vi vill nu bevisa denna följdsats. Du kommer inte att examineras på detta bevis. I beviset ingår en viktig detalj: Om man skall visa, att två mängder är lika, här att M=L, då visar man  (i) att M 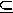L,  och (ii) att L 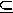M, och drar slutsatsen att M=L. Varför är detta sant? (Ledning: Rita Venndiagram!)

Bevis (följdsats B4.2).
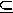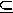För att visa, att de två mängderna M och L är lika, visar vi (i) att M L  och (ii) att L M:

(i) Sats B4.1 ger att g tillhör L. Så antag att s och t är sådana heltal att g= sm+tn. Då är multiplen

kg = k(sm + tn)=(ks)m + (kt)n
för varje heltal k. Därför är M 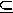L.

(ii) Låt nu j vara ett element i L, dvs. j=s₁m+t ₁n, där s₁ och t₁ är heltal. Eftersom g | m och g | n har vi ur sats 3.4 i [EG] att g | (s₁m+t₁n), så det existerar alltså ett heltal k sådant att (s₁m+t₁n) =kg; men det betyder att j också är ett element i M, så därför är L 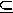M.   

Uppgift B4.3
Använd resultatet av Följdsats B4.2 för att hitta elementen i följande mängder
(a) L={x |  x=s3+t7,  s,t  };

(b) L={x |  x=s4+t6,  s,t  };

(c) L={x |  x=s6+t9,  s,t  }.

Svar!

Jämför dessa resultat med resultaten i uppgift B4.2.

3. Euklides algoritm

I  föregående avsnitt fann vi att om man vill hitta alla möjliga linjärkombinationer av två heltal (som inte båda är noll), så är det tillräckligt att känna till deras största gemensamma delare. I de exempel vi studerade, var det relativt lätt att hitta sgd(m,n), eftersom m och n var små tal; men om vi vill hitta sgd(m,n) där m och n är stora tal, t.ex.  sgd(15939,9367), vad göra?

Sats B4.1 garanterar att sgd(15939,9367) existerar, men den säger inte hur vi i praktiken hittar den största gemensamma delaren. Lyckligtsvis finns en gammal algoritm som är särskilt effektiv för att beräkna största gemensamma delaren till två heltal. Algoritmen går under namnet Euklides algoritm, då den finns beskriven i Euklides 'Elementa' (cirka 300 F. Kr.), och den är än idag den mest effektiva algoritm man känner till för detta syfte.

Euklides algoritm kan för övrigt också användas för att hitta en linjärkombination av två heltal som är lika med sgd(m,n).  Återigen garanterar sats B4.1, att en sådan linjärkombination existerar, men den säger inte, hur vi kan hitta den.

Vi ska i resten av detta avsnitt anta att m och n båda är positiva heltal. Vi förlorar inget på att anta detta, eftersom vi har följande sats:

Sats B4.3
Låt m och n vara heltal och antag att sgd(m,n) existerar. Då är sgd(m,n) =sgd(|m|,|n|).

Bevis.
Detta följer av, att om d | m, så har vi också att d | (-m) (Varför?). 

Euklides algoritm bygger på Divisionssatsen, som vi beskrev i avsnitt 1 i läsanvisningen till block 4.
Euklides algoritm är följande:

Euklides Algoritm

• Antag, att m och n är två positiva heltal, och att vi vill beräkna sgd(m,n).
• Använd först Divisionssatsen för att dela m med n,
  varvid vi får en rest r₁, där 0 r₁ <  n.
•  Om r₁ 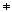0, då delar vi n med r₁ och får en rest r₂ , där 0   r₂ < r ₁.
•  Om r₂ 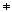0, då delar vi r₁ med r₂ och får en rest r₃ , där 0   r₃ < r ₂.
•  Om r₃ 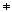0, då delar vi r₂ med r₃ och får en rest r₄ , där 0   r₄ < r ₃.
•  Om r₄ 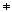0, då delar vi r₃ med r₄ och får en rest r₅ , där 0   r₅ < r ₄.

   .
   .
   .
 
• Så fortsätter vi, tills vi vid en tidpunkt får resten 0.
• Om denna rest är r_k, dvs. r_k=0 och r_i 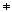0 for i < k,
  då är sgd(m,n)=r_k-1.
• sgd(m,n) är alltså den sista resten, som inte är noll.

Exempel
Låt oss använda Euklides algoritm för att hitta sgd(m,n) då m= 54  og n=33:

54 = 33(1) +  21   [dela m=54 med n=33, rest r₁ = 21]
33 = 21(1) +  12   [dela n= 33  med r₁=21, rest r₂=12]
21 = 12(1) +   9    [dela r₁=21 med r ₂=12, rest r₃= 9]
12 =   9(1) +   3    [dela r₂=12 med r₃=  9, rest r₄=3]
  9 =   3(3)           [dela r₃=  9 med r₄=  3, rest r₅ =0 ]

Enligt Euklides algoritm är sgd(54,33) = 3, dvs. den sista rest, som inte är noll.

Läs nu delavsnitt 3.3.4 i [EG]  från och med Metod 3.4 sidan 47 t.o.m. sidan 50. Här beskrivs Euklides algoritm igen,  och man förklarar hur den fungerar. Vi ger ytterligare ett exempel, denna gång försöker vi hitta största gemensamma delaren till två tal som inte omedelbart kan faktoriseras.

Exempel
Låt oss hitta sgd(15939, 9367) med hjälp av Euklides algoritm:

15939 = 9367(1) + 6572
  9367 = 6572(1) + 2795
  6572 = 2795(2) + 982
  2795 =   982(2) + 831
    982 =   831(1) + 151
    831 =   151(5) +   76
    151 =     76(1) +   75
      76 =     75(1) +     1
      75 =       1(75)

Så sgd(15939, 9367) =1.

När sgd(m, n) =1, så har talen m och n ingen gemensam delare förutom enheterna  1 och -1. Sådana heltal säges vara relativt prima. Observera att tal kan vara relativt prima, även om inget av dem är primtal, t.ex. är 12 och 35 relativt prima.  

Sats B4.4
Låt m och n vara heltal, som inte är noll.
Då är m och n relativt prima om och endast om det existerar två heltal a och b så att am + bn = 1.

Bevis
(==>) Antag, att m och n är relativt prima, dvs. sgd(m,n)=1. Sats B4.1 ger då, att det existerar heltal a och b sådana att sgd(m,n)=am+bn, dvs. 1 = am + bn.

(<==) Antag, att det existerar heltal a och b sådana att 1 = am + bn, och låt sgd(m,n)=s. Eftersom s | m och s | n, har vi ur Sats 3.4 i [EG] att s | am + bn, dvs. s | 1, och därför är s =-1 eller s=1. Utav definitionen av sgd har vi dock, att s är positiv, så därför kan vi konkludera, att s=1.   

Läs nu resten av delavsnitt 3.3.4, men ej 3.3.4.1.

Som nämnts ovan, kan Euklides algoritm användas för att hitta en linjärkombination av två heltal m och n som är lika med sgd(m,n).  Detta görs genom att först skriva om alla ekvationerna i algoritmen till att ge ett uttryck för resterna och arbeta sig upp genom algoritmen bakifrån. Detta illustreras lättast genom ett exempel:

Exempel
Vi fann ovan, att sgd(54, 33)= 3 i följande fyra steg, som vi först skriver som

54 = 33(1) +  21      ==>    21  = 54 - 33(1)
33 = 21(1) + 12       ==>    12  = 33 - 21(1)
21 = 12(1) +   9       ==>      9  = 21 - 12(1)
12 =   9(1) +   3       ==>      3  = 12 -   9(1).

Vi börjar med den fjärde ekvationen, som uttrycker sgd(54, 33)= 3 som en linjärkombination av 12 och 9. Därnäst substituerar vi den tredje ekvationen in i uttrycket, förenklar det, substituerar sedan den andra ekvationen in i uttrycket, förenklar igen, etc. :

3 = 12 + 9(-1)

   = 12 + [21-12(1)] (-1)       [här substituerar vi in 3. ekvationen]

   = 12(2) +21(-1)                 [förenkling ] [Koll: HL =24 - 21 = 3]

   = [33-21(1)](2)  + 21(-1)   [här substituerar vi in 2. ekvationen ]

   = 33(2) +21(-3)                 [förenkling ] [Koll: HL =66 - 63 = 3]

   = 33(2) +[54 -33(1)] (-3)   [här substituerar vi in 1. ekvationen]

   = 33(5) +54(-3)                 [förenkling ] [Koll: HL =165 - 162 = 3]

Från den sista ekvationen fås nu, att 3 = 54a + 33b, där a = -3  och b = 5.

Processen som beskrivs i detta exempel är inte särskilt svår, men det är mycket lätt att göra ett räknefel. Vi föreslår därför att alltid sätta runda parenteser omkring kvoter eller att stryka under alla rester, så att man kan se skillnad på kvoterna och resterna. Ett annat tips är att efter varje förenkling, kontrollera att högerledet är lika med den största gemensamma delaren, såsom vi har gjort i exemplet ovan. Om du följer dessa två huvudregler, skall det vara möjligt att göra dessa beräkningar utan fel.

4. Diofantiska ekvationer

Läs nu delavsnitt 3.3.5 i [EG], det handlar om diofantiska ekvationer.

Diofantiska ekvationer är ekvationer där man bara är intresserat att hitta heltalslösningar. Vi skall se på linjära diofantiska ekvationer, dessa är på formen ax+by=c där a,b,c,x och y är heltal.

Läs också följande text ur noter av Sarah Norell för kursen Diskret Matematik A för Datateknik (referenser är till satser ovan):

Diophantine equations

Example
Suppose you need to measure 1dl but only have two jugs which hold 10dl and 23dl respectively, a large container and a tap. Can it be done? This is the same as asking if there is an integer solution x,y to the equation 10x+23y=1. As gcd(23,10)=1, and there are integers s,t such that 23s+10t=gcd(23,10)=1, (by theorem B4.1 above) there is at least one solution, x=t and y=s to this equation. You saw above how this can be found by applying the Euclidean algorithm and then substituting back from the last equation with a non-zero remainder.

Example
If you replace the jugs by one which holds 10dl and another which holds 24dl, can it be done? In this case, we want an integer solution to the equation 10x+24y=1. Is there one? The answer is clearly no, because in Corollary B4.2 above we showed that only numbers divisible by the gcd(24,10) can be written as a linear combination of 24 and 10. To see why this is so: consider the left hand side of the equation. As both 24 and 10 are divisible by 2, if there is a solution then the left hand side of the equation is divisible by 2, and hence the right hand side is divisible by 2. This is a contradiction as 2 does not divide 1. Hence there are no integers solutions to 10x+24y=1.

So, what we have so far concerning whether there is an integer solution to ax+by=c or not is:

• If k | a and k | b but k does not divide c, there is no integer solution to ax+by=c.
• If c=gcd(a,b) then there is a solution and it can be found by working backwards through the equations obtained by applying the Euclidean algorithm.

What else might we want to know? What if c 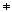gcd(a,b) but all common factors of a and b are also factors of c? If there is a solution, is it the only solution or are there many solutions?

Example
If you use Euclid's algorithm forwards and backwards, you can find that gcd(957, 426) =3 and that

3 = 69957 - 155426.

Suppose we want to find integers x and y so that

12 = 957x+426y.

Then we just need to take 4 times the first equation to get

34 = (694)957 + (-1554)426.

This means that x=694 and y=-1554 is one possible solution.

Using Euclid's algorithm in the same way on a and b of the general linear Diophantine equation ax+by=c we get that

• if d=gcd(a,b), d=as+bt and c=du: then x=su and y=tu is one possible integer solution.

This leads to our next theorem, which summarises our discussion so far.

Theorem B4.5
Let a,b,c be integers.
Then there are integer solutions x,y such that ax+by=c if and only if gcd(a,b) | c.

Proof
First we prove that if there are integers x and y such that ax+by=c then gcd(a,b) | c: Suppose ax+by=c where x and y are integers. Let d=gcd(a,b). Then d | a and d | b so d | (ax+by), that is d | c.

Now we prove that if gcd(a,b) | c. then there are integers x, y such that ax+by=c:
Let d=gcd(a,b), and suppose that d | c. Then there are integers s and t such that

d=sa+tb (1)

and integer u such that du=c. Multiplying (1) by u we get

c=du=(su)a+(tu)b.

As su and tu are integers, there are integers x=su and y=tu such that ax+by=c.

Example
I have 2004kr to invest in two different places. I can invest in A in blocks of 957kr and in B in blocks of 426kr. Can I invest all the money? If so, how?

We want to find solutions to 957x+426y=2004 where x is the number of blocks of A and 426 is the number of blocks of B. From above, we have

3=95769 + (-155)426.

As 2004=6334=3668, we have

2004=957(66869) + 426(-155668)

so x=46092 blocks of A and y=-103540 blocks of B. Err... buy a negative number of blocks? Obviously this is impossible, so we need to find out if there are any other solutions. We continue this example after the next theorem.

Theorem B4.6
Let a,b,c be integers.
If c=ax+by and x=x₀, y=y₀, is one solution, then
if t is any integer and d=gcd(a,b), we have that

x=x₀+t(b/d),

y=y₀ - t(a/d)

give all solutions.

Proof

• First we show that x=x₀+bt/d, y=y₀-at/d is a solution to ax+by=c, by substituting for x and y in ax+by. We get
  ax+by=a(x₀+bt/d)+b(y₀-at/d)= ax₀+abt/d+by₀-abt/d= ax₀+by₀=c,
  so x=x₀+bt/d, y=y₀-at/d is a solution.
• Next we show that every solution can be written in the form x=x₀+bt/d, y=y₀-at/d. Let x=x₁, y=y₁ be a solution. Then
  ax₁+by₁=c=ax₀+by₀.
  Rearranging gives
  a(x₁-x₀)=b(y₀-y₁.
  Now d=gcd(a,b) so there are integers s,t such that ds=a and dt=b. Note that gcd(s,t)=1. (Why?) We substitute for a and b to get
  ds(x₁-x₀)=dt(y₀-y₁).
  Cancelling d gives
  s(x₁-x₀)=t(y₀-y₁)     (1).
  Now s | t(y₀-y₁), and as gcd(s,t)=1, s | (y₀-y₁). Hence su= y₀-y₁ for some integer u. Substituting this in (1) gives in (1)
  s(x₁-x₀)=tsu
  so
  x₁-x₀=tu
  Rearranging and putting s=a/d and t=b/d gives
  x₁=x₀+bu/d
  y₁=y₀-au/d
  as required.

Example (continued)
The general solution is x=46092 + 426/3 t and y=-103540 - 957/3 t where t is an integer.
[We can think of this as follows:

where t is an integer.]

We need the values of t for which x and y are non-negative:

Rearranging gives t -46092/142 ~ -324.59 from (1) and t 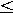-103540/319 ~ -324.58 from (2). Unfortunately there are no integer values within this range so there is no feasible solution to my problem.

Now let's try a problem which does have a solution.

Example
In order to take part in a race, there is an entrance fee of 27kr for children and 38kr for adults. This fee includes a medal for every adult and every child. Unfortunately, when the secretary was about to order the medals, he discovered that he had only the total amount, 3725kr which had been paid. What is the smallest number of adult medals and the smallest number of children's medals he should order to be sure that he has enough of each type?

Solution

• We want to solve 27x+38y=3725 where x is the number of children's tickets and y is the number of adult tickets. Of course, x and y must be non-negative.
• First we find the greatest common divisor of 38 and 27, using the Euclidean algorith. We get 38=27+11, 27=211+5, 11=25+1, 5=51. So gcd(38,27)=1. As gcd(38,27)=1 which is a divisor of 3725, there is an integer solution to 27x+38y=3725.
• Now we find integers s,t such that 1=38s+27t by subsituting into the equations above. We get
  1=11-25= 11-2(27-211)= 511 -227= 5(38-27)-227
  = 538 -727.
  So t=-7 and s=5.
• We use the solution above to obtain a solution to 3725=27x+38y, by multiplying the solution above by 3725. This gives a particular solution of x=-73725=-26075 and y=53725=18625
• Now we find all solutions, ignoring the non-negativity demand:
  x=-26075+38/1 u and y=18625-27/1 u where u is an integer.
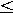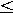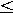• Now we require values of u for which x and y are non-negative, that is -26075+38u 0 and 18625-27u 0. These give us u 26075/38 ~ 686.18 and u 18625/27 ~ 689.81. These give 687 u 689
  [Make sure you include the correct integers when you round up or down.]
  So the feasible solutions are
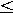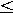  x=-26075+38u and y=18625-27u where u is an integer and 687 u 689
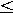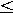• Now the numbers above are rather large so we put w=u-687, so 0 u 2