Modulär aritmetik.

Referenser

[EG]   avsnitt 3.4;
och nedanstående text.

Nyckelord

Kongruens modulo n, kongruensklasser modulo n. Z_n - heltalen modulo n, additions- och multiplikationstabellen för Z_n. Räknelagar för Z_n. Nolldelare. Den multiplikativa inversen till ett element i Z_n och hur man använnar Euklides algoritm till at hitta den multiplikativa inversen. Lösning av ekvationer i Z_n.

Inledning

I detta block skall vi titta på modulär aritmetik, som är ett viktigt redskap när man studerar heltal. Börja med att läsa inledningen till avsnitt 3.4 i [EG] sidan 58 - 60, som är en bra introduktion till moduloräkning. Läs sedan avsnitt 1 och 2 nedan.
 

1. Kongruens modulo n

Vi börjar med en viktig definition som inte finns i avsnitt 3.4 i [EG], den formella definitionen av kongruens modulo n:

Definition
Låt n vara ett positivt heltal. Heltalen a och b sägs vara kongruenta modulo n om n är en faktor i a-b eller med andra ord om

n | (a-b).
Om a och b är kongruenta modulo n skriver vi

a  b  (mod n),

vilket utläses som 'a är kongruent med b modulo n'.

Exempel
 12    22     42    2 (mod 10)

-18  -38     -8    2 (mod 10)

12    19     -9    5 (mod 7)

  7      5     3     1 (mod 2)

  6      4      2     0 (mod 2)
 
 

Notera till att börja med, att n | (a-b) om och endast om vi kan finna en kvot k i  sådan att a - b = kn.

Vidare, när a - b =kn för något heltal k så ger a och b samma rest vid division med n:
Antag att a=q₁n + r₁ och b=q₂n + r₂ med 0  r₁ < n och 0  r₂ < n. Då är

a - b = (q₁ - q₂)n + (r₁ - r₂),

som omskrivas till r₁ - r₂ = (a - b) - (q₁ - q₂)n =kn - (q₁ - q₂)n = (k - q₁ + q₂)n.

Höger sida av detta uttryck innehåller en faktor n, så n måste också vara en faktor i vänster sida, så n | r₁-r₂.
Men -n < r₁ - r₂ < n, så det följer att r₁ - r₂ = 0, så r₁=r₂ .

Omvänt gäller också att om a och b ger samma rest vid division med n, så följer att n | (a-b):
Om a=q₁n + r och b=q₂n + r, så är a - b =(q ₁ - q₂)n + (r - r) = (q₁ - q₂)n. Vi har alltså följande tre resultat:

Sats B5.1
a  b  (mod n) om och endast om det finns ett heltal k så att a-b =kn.

Sats B5.2
a  b  (mod n) om och endast om det finns ett heltal k så att a = b + kn.

Sats B5.3
a  b  (mod n) om och endast om a och b ger samma rest vid division med n.

Dessa tre resultat bygger alla på en av de viktigaste satser vi har lärt oss  (i block 4):

Divisionssatsen
Givet ett godtyckligt heltal a och ett positivt heltal n, så existerar det entydigt bestämda heltal k och r sådana att

a=kn + r      och     0  r   n-1.

Översatt till kongruenser mellan heltal så betyder denna sats att det finns ett entydigt bestämt heltal r i mängden
{0, 1, 2, 3, 4, . . . , n-1} sådan att a  r  (mod n).  En del programmeringsspråk, t.ex. Pascal har en standard funktion MOD som beräknar denna entydigt bestämda rest. I Java finns funktionen också, men betecknas '%'.

Exempel
Låt oss beräkna det entydigt bestämda heltal r så att
a r  (mod n)  och   0  r  n-1,  när

(a) n = 5 och a = 448;
(b) n = 5  och a= - 63;
(c) n = 4 och a=17, -17;
(d) n = 2 och a är ett jämnt/udda heltal.

Svar:
(a) När vi dividerar 448 med 5 får vi kvoten 89 och resten 3, d.v.s. 448= 5(89) +3
     så r=3 och 448  3 (mod 5) med 0  3  4 som vi vill.

(b) När vi dividerar -63 med 5 får vi kvoten -13 och resten 2, d.v.s. -63= 5(-13) +2
     så r=2 och -63  2 (mod 5) med 0  2  4.

(c) När vi dividerar 17 med 4 får vi kvoten 4 och resten 1, d.v.s. 17= 4(4) +1
     så r=1 och 17  1 (mod 4) med 0  1  3.

     När vi dividerar -17 med 4 får vi kvoten -5 och resten 3, d.v.s -17= 4(-5) +3
     så r=3 och -17  3 (mod 4) med 0  3  3.

(d) När vi dividerer ett jämnt tal 2k med 2 får vi kvoten k och resten 0, d.v.s. 2k= 2(k) +0,
     så r=0 och 2k  0 (mod 2) med 0  0  1.

     När vi dividerar ett udda tal 2k+1 med 2 får vi kvoten k och resten 1, d.v.s. 2k+1= 2(k) +1
     så r=1 och 2k +1  1 (mod 2) med 0  1  1.
 

Exempel
Låt oss nu göra det motsatta och bestämma mängden av alla heltal som är kongruenta modulo 5 med vart och ett av talen 0, 1, 2, 3 och 4:
 

• Mängden av heltal a sådana att a  0 (mod 5) är

{. . ., -15, -10, -5, 0, 5, 10, 15, . . .} = {x | x=5z, z  }

• Mängden av heltal a sådana att a  1 (mod 5) är

{. . ., -14,   -9, -4, 1, 6, 11, 16, . . .} = {x | x=5z+1, z  }

• Mängden av heltal a sådana att a  2 (mod 5) är

{. . ., -13,   -8, -3, 2, 7, 12, 17, . . .} = {x | x=5z+2, z  }

• Mängden av heltal a sådana att a  3 (mod 5) är

{. . ., -12,   -7, -2, 3, 8, 13, 18, . . .} = {x | x=5z+3, z  }

• Mängden av heltal a sådana att a  4 (mod 5) är

{. . ., -11,   -6, -1, 4, 9, 14, 19, . . .} = {x | x=5z+4, z  }

Notera att alla heltal i var och en av de fem mängderna ger samma rest vid division med 5, så i en och samma mängd är varje par av element därför kongruenta modulo 5. Notera också att varje heltal är i en och endast en av dessa mängder. Dvs. de fem mängderna partitionerar .

Mängden av heltal a sådana att a  b  (mod n)  kallas för kongruensklassen modulo n med representanten b.
Vi använder beteckningen [b]_n för kongruensklassen som innehåller alla a sådana att a  b  (mod n). När det av sammanhanget klart framgår vad n är, kan vi bortse från indexet n i denna notation och endast skriva [b] för kongruensklassen modulo n med representanten b.

Exempel
Låt oss bestämma några kongruensklasser modulo 10 med diverse representanter:

[3]₁₀ = {. . ., -27,   -17, -7, 3, 13, 23, 33, . . .},

[5]₁₀ = {. . ., -25,   -15, -5, 5, 15, 25, 35, . . .},

[12]₁₀ = {. . ., -28,   -18, -8, 2, 12, 22, 32, . . .},

[43]₁₀ = {. . ., -27,   -17, -7, 3, 13, 23, 33, 43, . . .}.

[-2]₁₀ =  {. . . , -32, -22, -12, -2, 8, 18, 28, 38, . . .}

Vid en snabb blick verkar det finnas oändligt många kongruensklasser modulo n (en för varje representant ur  ). Detta är inte fallet, för många av dem är lika. Till exempel är  [43]₁₀ =[3]₁₀. För n=5 vet vi också från det föregående exemplet, att eftersom alla heltal är i en av de fem mängderna vi beräknade, är det precis fem kongruensklasser modulo 5, en svarande till var och en de fem möjliga resterna vid division med 5.

Allmänt finns det precis n kongruensklasser modulo n, nämligen en klass svarande mot var och en av de n möjliga resterna 0,1, ... n-1 som kan uppkomma vid division med n. Det vanliga är att ett av talen 0,1,2, . . . , n-1 används som representant för kongruensklassen, men det är inte absolut nödvändigt: ett godtyckligt element i kongruensklassen kan användas som representant. Till exempel så skrivs mängden {. . ., -28,   -18, -8, 2, 12, 22, 32, . . .} vanligen med [2]₁₀ för 2 är den entydigt bestämda resten i divisionssatsen, men som du såg i exemplet ovan är [12]₁₀ precis samma mängd.

Exempel
Tidigare beräknade vi för n = 5:

[0] =  {x | x=5z, z },

[1] =  {x | x=5z+1, z },

[2] =  {x | x=5z+2, z },

[3] =  {x | x=5z+3, z },

[4] =  {x | x=5z+4, z },

men vi skulle också kunna representera t.ex. kongruensklassen {x | x=5z+2, z  } med [7]
och klassen {x | x=5z+1, z  } med [6] eller [-4] eller [-9] eller . . .

Uppgift B5.1
Sant eller falskt?

1. 811 (mod 8);


2. 811 (mod 10);


3. 1124 (mod 11);


4. 1000-1 (mod 13);


5. 990 (mod 5);


6. 93737 (mod 100);


7. För godtyckliga heltal a, b, c och m; om a b (mod m), så är a = b;


8. Om ab (mod m), så är a+c b+c (mod m);


9. Om ab (mod m), så är ac bc (mod m).

Uppgift B5.2
Bestäm alla heltal x sådana att x 3 (mod 5).

2. Z_n -- heltalen modulo n

Vi såg i avsnitt 1 ovan att kongruens modulo n ger n kongruensklasser [0], [1], [2], . . . , [n-1] sådana att varje heltal finns i precis en av dessa klasser. Vi definierar nu mängden Z_n , som läses heltalen modulo n, till att vara mängden bestående av dessa n kongruensklasser, d.v.s.

Z_n =  {[0]_n, [1]_n, [2] _n, . . . , [n-1]_n}. Om det klart framgår av sammanhanget vilket talet n är kommer vi endast att skriva [x] för ekvivalensklassen [x]_n. Heltalen modulo n skrivs då Z_n =  {[0], [1], [2], . . . , [n-1]}. Och när vi har lärt oss se skillnad på heltal och kongruensklasser, kan vi helt ta bort parenteserna och skriva

Z_n =  {0, 1, 2, . . . , n-1}.

Vi kan definiera en slags addition, som vi betecknar med  , och en slags multiplikation, som vi betecknar med  , på Z_n:

[x]  [y] := [x+y],
[x]  [y] := [xy].

Notera att resultatet vid utförande av operationerna  eller  på två element i Z_n är ett element i Z_n för vi visade i avsnitt 1, att for varje heltal x är klassen [x]_n ett av de n elementen i Z_n . Vi har också följande viktiga resultat:

Sats B5.4
Låt x, y, s och t vara heltal och låt n vara ett positivt heltal. Om s  [x]_n och t  [y]_n , så är
s+t  [x+y]_n och st  [xy]_n.

Bevis.
Om s  [x]_n och t  [y]_n, så är s  x (mod n) och t  y (mod n). Det vill säga n | (s-x) och n | (t-y), så det existerar alltså heltal k och m sådana att s-x=kn och t-y=mn. Men då är

(s - x) + (t - y) = kn + mn, och detta kan skrivas om till (s + t) - (x + y) =(k+m)n, varav det inses att (s + t)  (x + y) (mod n), eller med andra ord s+t  [x+y]_n .

Vi får också

(s - x)(t - y) =(kn)(mn), som ger att (kn)(mn)= st + xy - xt - ys= st + xy - x(y + mn) - y(x + kn) = st - xy - (xm + yk)n, vilket kan skrivas om till st - xy = (knm + xm + yk)n. Det följer att st  xy (mod n), så st  [xy]_n.  

Sats B5.4 säger att om s   [x]_n och t  [y]_n, så är [s+t]_n = [x+y]_n,  och [st] _n = [xy]_n,  vilket betyder att inte bara klasserna, utan också definitionerna av  och  är oberoende av valet av klassrepresentant.

Det finns många grundläggande lagar som gäller för de två operationerna  och . Du känner säkert igen de flesta av dem som har motsvarigheter i liknande räknelagar för heltal.
 

Sats B5.5
Om Z_n  är mängden av kongruensklasser modulo n och  och  är definierade som ovan, så uppfyller Z_n  följande:

1. Slutenhet. För alla [x], [y]  Z_n gäller att
         [x]  [y]  Z_n och
         [x]  [y]  Z_n.
2. Associativa lagar. För alla  [x], [y], [z]  Z_n gäller att
        [x]  ([y]  [z]) = ( [x]  [y])  [z]   och
        [x]  ([y] [z]) = ([x]  [y])  [z].

3. Identiteter existerar.
        Det existerar ett element [0]  Z_n   sådant att för alla  [x]  Z_n  har vi att
             [x]  [0] =[0]  [x] = [x].

        Det existerar också ett element [1]  Z_n , med [1] 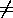 [0],  sådant att för alla  [x] Z _n har vi att
             [x]  [1] = [1]  [x] = [x].

4. Additiva inverser existerar. För alla [x]  Z_n har vi att
      det existerar en additiv invers  [-x]  Z_n   som uppfyller att
             [x]  [-x] =[-x]  [x] = [0].

5. Kommutativa lagar. För alla  [x],[y]  Z_n så gäller att
        [x]  [y] = [y]  [x] och
        [x]  [y] = [y]  [x] .

6. Distributiva lagar. För alla [x],[y],[z]  Z_n gäller att
        [x] ([y]  [z]) = ([x] [y])   ([x] [z])  och

       ([y] [z])  [x] = ([y] [x])    ([z] [x]).
 

Bevis.
Vi resonerade tidigare om varför den första lagen gäller. Vi visar nu de associativa lagarna (lag 2) och lagen om existens av additiv invers (lag 4). De andra bevisen överlåter vi till läsaren.

Först visar vi att  är associativ:

([x]  [y])  [z]	=	[x+y]  [z]		(från definitionen av )
	=	[(x+y) + z]		(igen med definitionen av )
	=	[x+ (y+z)]		(för att + är associativ på )
	=	[x]  [y+z]		(från definitionen av )
	=	[x]  ([y]  [z])		(igen med definitionen av )

Därnäst visar vi att  är associativ:

([x]  [y])  [z]	=	[xy]  [z]		(från definitionen av )
	=	[(xy)z]		(igen med definitionen av )
	=	[x(yz)]		(för att + är associativ på )
	=	[x]  [yz]		(från definitionen av )
	=	[x]  ([y]  [z])		(igen med definitionen av )

Med lag 4 har vi från definitionen av , att det för alla [x]  Z _n gäller att

[x]  [n-x] = [n-x]  [x] = [n] = [0]. Det innebär att klassen [n-x] är en additiv invers till [x]. 
 

Låt oss nu konstruera additions- och multiplikationstabeller för Z_n för några värden på n:

Exempel
Additionstabellen för Z₄ är:

	[0]	[1]	[2]	[3]
[0]	[0]	[1]	[2]	[3]
[1]	[1]	[2]	[3]	[0]
[2]	[2]	[3]	[0]	[1]
[3]	[3]	[0]	[1]	[2]

Multiplikationstabellen för Z₄ är:

	[0]	[1]	[2]	[3]
[0]	[0]	[0]	[0]	[0]
[1]	[0]	[1]	[2]	[3]
[2]	[0]	[2]	[0]	[2]
[3]	[0]	[3]	[2]	[1]

Exempel
Additionstabellen för Z₅ är:

	[0]	[1]	[2]	[3]	[4]
[0]	[0]	[1]	[2]	[3]	[4]
[1]	[1]	[2]	[3]	[4]	[0]
[2]	[2]	[3]	[4]	[0]	[1]
[3]	[3]	[4]	[0]	[1]	[2]
[4]	[4]	[0]	[1]	[2]	[3]

Multiplikationstabellen för Z₅ är:

	[0]	[1]	[2]	[3]	[4]
[0]	[0]	[0]	[0]	[0]	[0]
[1]	[0]	[1]	[2]	[3]	[4]
[2]	[0]	[2]	[4]	[1]	[3]
[3]	[0]	[3]	[1]	[4]	[2]
[4]	[0]	[4]	[3]	[2]	[1]

Många av räknelagarna i sats B5.5 kan lätt läsas av i dessa tabeller. Till exempel visas de kommutativa lagarna av att tabellerna är symmetriska omkring huvuddiagonalen. Man ser också att [0] är en additiv identitet och att [1] är en multiplikativ identitet, ty raden för [0] i additionstabellen och raden för [1] i multiplikationstabellen har alla element i naturlig ordningsföljd. Vidare är det precis ett element [0] i varje rad i additionstabellen svarendes mot att det för en godtycklig klass [x] finns precis en klass [y] sådan att  [x]  [y] = [0] - detta är lagen om existens av additiv invers.

Vi noterar också att Z₅  har några egenskaper som Z₄  inte har:

I multiplikationstabellen för Z₅  är det precis en [1] och precis en [0] i varje rad och varje kolonn. Detta är inte fallet i multiplikationstabellen för Z₄ , i vilken det inte finns någon [1] i raden eller kolonnen för [2], medan det finns två [0] i denna rad/kolonn. Elementet [2]  Z₄ kallas en nolldelare.

Definition
Vi definerar en nolldelare i Z_n till att vara ett element [z]  Z_n med [z] 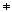 [0]
för vilket det existerer ett element [m]  Z_n med [m]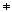 [0] sådant att [z]  [m] =[0].

Exempel
Om man sätter z=2 och m=2 i denna definition ser man att  [2]  är en nolldelare i Z₄.

De reella talen 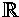, de rationella talen  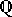och heltalen  uppfyller en mycket viktig lag som kallas lagen om nolldelare. Den säger att dessa talmängder inte innehåller nolldelare. Om man t. ex. har två reella tal r och s sådana att rs=0, så är antingen r=0 eller s=0 (eller de är bägge 0). För de reella talen 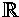 är det därför inte möjligt att ha två tal båda skilda från noll med produkten noll. Vi använder ofta denna lag vid lösning av ekvationer. Resonemang i stil med följande exempel känner du säkert igen:

(x-2)(x-4)=0      =>     (x-2)=0 eller (x-4)=0      =>     x=2 eller x=4.

Ur multiplikationstabellen för Z₅ ser vi att Z₅  också uppfyller lagen om nolldelare. Det är ingen produkt av element i Z₅ som är [0] utan att minst en av faktorerna är [0]. Vi noterade ovan att Z ₄  har en nolldelare, för

[2]₄ [2]₄ =[0]₄, det vill säga Z₄ uppfyller inte lagen om nolldelare.

Uppgift B5.3
Beräkna multiplikationstabellerna för Z₂, Z₃, Z₆, Z₇, Z₈ och Z₉.  I vilka av dessa är lagen om nolldelare giltig och i vilka håller den inte? Kan du gissa för vilka n lagen on nolldelare gäller i Z_n?

Vi hoppas att ditt svar till uppgift B5.3 stämmer överens med följande sats:

Sats B5.6
Låt n vara ett heltal sådant att n  2 och låt Z_n vara mängden av kongruensklasser (mod n).
Då finns det ingen nolldelare i Z_n om och endast om n är ett primtal.

Bevis
Antag först att n=p där p är ett positivt primtal och att [x]  [y] =[0] i Z_p. Eftersom [x]  [y] =[xy] har vi att [xy] =[0], dvs. xy  0 (mod p), och därför gäller att p | xy. Men då följer det av sats B3.8 från läsanvisningen till block 4 att p | x eller p | y, dvs. [x] =[0]  eller  [y] =[0]. Så när n är ett positivt primtal, då finns det ingen nolldelare i Z _n.

När n däremot inte är ett primtal så är n ett sammansatt tal och vi kan därför uttrycka n som en produkt av två äkta faktorer a och b, dvs.

n=ab,
med 2  a n-1 och 2  b n-1. Då är [a]_n [b]_n = [ab]_n = [n]_n = [0]_n,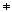 och både [a]_n   [0]_n  och  [b]_n 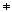[0]_n,  så  [a]_n (och också [b]_n ) är en nolldelare i Z_n. 

Vid lösning av ekvationer med reella tal användes ofta möjligheten att det är tillåtet att förkorta med en faktor skild från 0 på båda sidor av likhetstecknet. Har vi till exempel för x  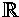 att 3x= 3·2 så kan vi dra följande slutsats:

3x = 3·2   =>  x=2, dvs. vi delar med en faktor 3 på båda sidor av likhetstecknet.

Om p är ett primtal fungerar en motsvarande förkortningslag i Z_p:

Följdsats B5.7 [Förkortningsregeln]
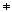Låt p vara ett positivt primtal och anta att klassen [a] Z_p  är sådan att [a] [0].
För alla klasser [x], [y]  Z_p  gäller att, om [a] [x] = [a] [y]  så är  [x] = [y].

Bevis.
Om [a]  [x] = [a] [y], så har vi att  [ax]=[ay] . Det följer att ax  ay (mod  p),  så p | (ax-ay).
Dvs. [0] = [ax-ay] = [a]  [x-y] och sats B5.6 säger då att   [a]=[0]  eller  [x-y]=[0]. Med antagandet att [a] 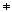 [0] så måste [x-y]=[0] vilket medför att p | (x-y). Dette ger nu att x  y (mod  p) vilket är detsamma som att   [x] = [y] . 

Var aktsam på att förkortningsregeln inte gäller i Z_n om n är ett sammansatt tal:
Låt n=ab vara en faktorisering av n i två äkta faktorer, så är [a]  [b] = [0]; men även [a]  [0] = [0], så vi har alltså att

[a]  [b] =  [a]  [0].
Trots detta är det inte så att [b] = [0] ty  b är en äkta faktor i n, så 1 < b < n.
 

De reella talen 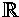 och de rationella talen  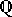har en annan viktig egenskap som vi också ofta använder när vi löser ekvationer. Det är egenskapen att varje tal skilt från 0 har en såkallad multiplikativ invers. En multiplikativ invers till ett tal r är ett tal s sådant att rs = sr = 1. Det reella talet 0,5 är en multiplikativ invers till 2 eftersom (0,5)·2 = 2·(0,5) =1, och vi kan till exempel använda detta vid lösning av ekvationen 2x =6 på följande sätt:

2x = 6     =>    (0,5)·(2x) = (0,5)·6     =>   ((0,5)·2)x = (0,5)·6    =>    1·x = 3    =>    x=3.

På liknande sätt definierar vi:

Definition
En multiplikativ invers till [x]  Z_n, där [x]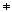 [0], är ett element [m]  Z_n med egenskapen att

[x]  [m]  = [m]  [x] = [1].

Vi såg i multiplikationstabellen för Z₄ tidigare att [2]₄ inte har en multiplikativ invers, ty det finns inte något element i Z₄ som ger [1]₄ när vi multiplicerar det med  [2]₄. I Z₅ däremot har varje element som inte är [0]₅ en multiplikativ invers, ty i multiplikationstabellen för Z₅ ser vi att varje rad utom för [0] ₅ innehåller [1]₅. Allmänt gäller det följande:
 

Sats B5.8
Låt n  vara ett positivt heltal med n  2 och låt [x]  Z _n vara skilt från [0].
Då har [x] en multiplikativ invers i Z_n om och endast om sgd(x,n) = 1.
Det gäller ytterligare att om det existerar en multiplikativ invers till [x], så är denna invers unik.

Bevis.
Om sgd(x,n) = 1 så finns det (enligt sats B3.7 från läsanvisningen till block 4) heltal a och b
sådana att ax+bn=1. Det vill säga bn = 1 - ax och vi har därför att ax  1 (mod  n).
Detta betyder att i Z_n har vi [a]  [x] = [1]. Alltså är [a] en multiplikativ invers till [x]  i Z_n.

Omvänt, om det existerar ett element [m]  Z_n sådant att   [x] [m] = [m] [x] = [1], då är
xm  1 (mod  n) och därför har vi att n | (xm - 1). Dvs. det finns ett heltal  r  sådant att  rn = xm - 1 och alltså är

1 = xm - nr. Eftersom sgd(x,n) delar både x och n, är högra sidan av detta uttryck delbart med sgd(x,n). Det följer att
sgd(x,n) också delar vänstra sidan av utrycket, det vill säga att sgd(x,n) delar 1. Men största gemensamma delaren är alltid ett positivt tal, och 1 har endast delarna -1 och 1, alltså kan vi dra slutsatsen att sgd(x,n)=1.

Att visa att inversen är unik är uppgift B5.7 nedan.

Exempel
Bestäm den multiplikativa inversen till [1753]  i Z₃₅₇₁.
Lösning:
(a) Använd först Euklides algoritme för att visa att sgd(1753, 3571)=1:

3571 = 1753(2) + 65
1753 =   65(26) + 63
    65 =     63(1) + 2
    63 =     2(31) + 1
      2 =     1(2)   + 0

Så sgd(1753, 3571) = 1.

(b) Använd sedan Euklides algoritme baklänges för at hitta heltal s och t sådana att 1753s + 3571t=1:
    1 = 63 + 2(-31)
       = 63 + (65-63)(-31)
       = 63(32) + 65(-31)
       = (1753 - 65(26))(32) + 65(-31)
       = 1753(32) + 65(-863)
       = 1753(32) + (3571-1753(2))(-863)
       = 1753(1758) + 3571(-863)

(c) Av beviset för Sats B5.8 fås då att [s] = [1758] är den multiplikativa inversen till [1753]  i Z₃₅₇₁.

(d) Koll: (1753)(1758) = 3081774 = 1 + 3571(863), så [1753]  [1758]= [1] i Z₃₅₇₁.

Uppgift B5.4
Låt  n=10. Bestäm alla tal  x  { 0,1,2, . . . ,9} sådana att sgd(x,10) = 1. För vart och ett av dessa tal använd Euklides algoritm för att bestämma tal  a, b  sådana att 1=ax + b(10), och sedan [y]  Z₁₀ sådant att [x]  [y]= [1].

Uppgift B5.5
Bestäm den multiplikativa inversen till
(a)   [5]  i Z₁₂;
(b)   [22]  i Z₃₁;
(c)   [10]  i Z₂₃;
(d)   [14]  i Z₂₅.

Uppgift B5.6
Visa för varje heltal n  2 att om [x] är en nolldelare i Z_n, så har [x] inte någon multiplikativ invers.
 

Uppgift B5.7
Visa m.h.a. Förkortningsregeln, att den multiplikativa inversen i Sats B5.8 är unik.

I delavsnitt 3.4.1 i [EG] definieras räkning i Z_n på ett mer oformellt sätt, läs nu delavsnitt 3.4.1 i [EG] och sedan avsnitt 3 nedan.

3. Ekvationer modulo n

I detta avsnitt skall vi lära oss bestämma alla möjliga lösningar x  till kongruenser på formen

 ax  b (mod  n) och alla möjliga lösningar [x]  Z_n till ekvationer  [a]  [x] =[b], där a,b och n är heltal och n 2.

Det är värt att notera att element  [x]  Z_n, som uppfyller [a]  [x] =[1],  motsvarar element x  {1, . . . , n-1}, som löser kongruensen  ax  1 (mod  n ). Detta används mycket ofta i bevisen för satserna som följer.

Sats B5.9
Kongruensen ax 1 (mod  n) har lösningar x  om och endast om sgd(a,n) = 1.
Det gäller ytterligare, att alla lösningar är kongruenta modulo n.
 

Bevis.
Om sgd(a,n) =1 så finns heltal s och t sådana att sa + tn = 1. Av beviset till sats B5.8 ser vi att lösningarna till  kongruensen ax  1 (mod  n) är alla element x i klassen [s].
Om däremot sgd(a,n) 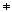 1, så har kongruensen inga lösningar, för en lösning skulle betyda, att det existerar en multiplikativ invers till [a] i Z_n, vilket är omöjligt enligt sats B5.8.
 

Uppgift B5.8
Antag att a, b och n är heltal sådana att n  2 och sgd(a,n) =1. Visa att om ax  1 (mod n), så är  a(bx)  b (mod  n), dvs. visa att om y = x löser kongruensen ay 1 (mod n), så löser bx kongruensen ay b (mod  n).
 

Uppgift B5.9
Använd din lösning till uppgift B5.5(a) för att bestämma en lösning till kongruensen 5x  1 (mod  12) och bestäm sedan en lösning till kongruensen 5x   4 (mod  12).

Om sgd(a,n) 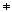 1, så har kongruensen ax  b (mod  n) antingen ingen lösning eller också så löser alla tal i en eller flera kongruensklasser modulo n kongruensen. Följande sats talar om när det finns lösningar och vilka de i sådant fall är.

Sats B5.10
Låt a, b och n vara heltal sådana att n  2 och sgd(a,n) =s.
Om  s | b, så har ekvationen

[a]  [x] = [b] s lösningar i Z_n, nämligen
[x] = [(b/s) x₀  + t(n/s)],
där t = 0, 1, . . . , s-1, och x₀ { 0, 1, . . . , (n/s) -1} är en lösning till den reducerade kongruensen (a/s)x  1 (mod  (n/s)).
Om s 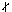 b, så har ekvationen inga lösningar.

Bevis.
Om [a]_n [x]_n = [b]_n  har en lösning [x]_n Z_n, så har vi att n | (ax-b), och genom att s | n  och  s | ax,  följer det att
att s | b. Så om s 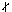 b kan det inte finnas någon lösning.

Antag nu att s | b.
Vid insättning ser man genast att om  x₀  löser kongruensen (a/s)x  1 (mod  (n/s)), så är de  s  kongruensklasserna
[x]_n = [(b/s)x₀ + t(n/s)]_n där t = 0, 1, ..., s-1 lösningar till ekvationen

[a]_n [x]_n = [b]_n.        (*)

Vi behöver då bara visa två saker:
(i) Varje lösning till ekvationen (*) kan skrivas på formen [x]_n = [(b/s)x₀ + t(n/s)]_n för något t .
(ii) Ekvationen (*) har precis  s lösningar.

För (i): Antag att  [x]_n  är en lösning till (*). Det finns då ett heltal k sådant att ax=b+kn, och eftersom s | a, s | b  och s | n, har vi vidare att

 (a/s)x  (b/s)  (mod  (n/s)). Detta betyder att i Z_n/s har vi likheten  [a/s]  [x] = [b/s].           (**) Enligt sats B5.8 har [a/s]  en entydigt bestämd multiplikativ invers  [x₀] i Z_n/s. Om vi då multiplicerar med  [x₀] på båda sidor av likheten (**), får vi att i Z_n/s gäller det att  [x] = [(b/s)x₀]. Detta innebär att för något t  är  x = (b/s)x₀ + t(n/s), vilket är x skriven i den önskade formen.
 

För (ii): Det finns som mest s kongruensklasser [(b/s)x₀ + r(n/s)]_n, nämligen en för varje r = 0,1,2, ... , s-1, för om
r 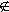 {0,1, . . . , s-1 }, så kan man med divisionssatsen få fram ett r₀ {0,1, . . . , s-1} sådant att r = qs + r₀.
Men [(b/s)x₀ + r(n/s)]_n = [(b/s)x₀  + r₀ (n/s)]_n, så r₀  ger precis samma kongruensklass som  r.

Det är också minst s kongruensklasser [(b/s)x₀ + r(n/s)]_n:
Antag att [(b/s)x₀ + r(n/s)]_n = [(b/s)x₀ + t(n/s)]_n, med  r, t  och s-1   t > r 0, då är

 (t-r)(n/s) = zn,  för något z , vilket strider mot att 0 < t-r < s.
Det finns alltså precis s sådana kongruensklasser. 
 

Exempel (Viktigt!)
Bestäm alla lösningar i  Z₇ till ekvationen  [5]  [x] = [2].

Lösning:

1. sgd(5,7)=1.
   Det finns alltså precis 1 kongruensklass i Z₇ som är lösning till ekvationen.


2. Den reducerade kongruensen är (5/1)x  2/1 (mod  (7/1)), som i Z_7/1 motsvaras av ekvationen  [5/1]  [x] = [2/1]. (Denna ekvationen var alltså redan reducerad!)


3. Bestäm nu den multiplikativa inversen till  [5/1]  i Z₇ med Euklides algoritm:
   7=5(1) +2
   5=2(2)+1.
   Så 1 = 5 + 2(-2) = 5 + [7 - 5](-2) = 5(3) + 7(-2),
   och [3] är då den multiplikativa inversen till  [5]  i Z₇.


4. Lösningen till den reducerade ekvationen fås nu genom att multiplicera ekvationen med multiplikativa inversen:  [3] [5]  [x] = [3] [2]. Men [3] [5] =[1], så detta ger  [1]  [x] = [6], så [x] = [6] är lösningen till den reducerade ekvationen.


5. Eftersom ekvationen i detta exempel var samma som reducerade ekvationen är lösningen till ekvationen också
   [x] = [6].
   (Lösningen till ekvationen fås i vanliga fall av Sats B5.10:
   [x] = [(2/1)3 + t(7/1)] där t=0, så [x] = [6].)  

Exempel (Viktigt!)
Bestäm alla lösningar i  Z₁₄ till ekvationen  [10]  [x] = [4].

Lösning:

1. sgd(10,14)=2.
   Det finns alltså precis 2 kongruensklasser i Z₁₄ som är lösning till ekvationen.


2. Den reducerade kongruensen är (10/2)x  4/2 (mod  (14/2)), som i Z₇ motsvaras av den reducerade ekvationen  [5]  [x] = [2].


3. Bestäm nu den multiplikativa inversen till  [5]  i Z₇ med Euklides algoritm:
   7=5(1) +2
   5=2(2)+1.
   Så 1 = 5 + 2(-2) = 5 + [7 - 5](-2) = 5(3) + 7(-2),
   och [3] är då den multiplikativa inversen till  [5]  i Z₇.


4. Lösningen till den reducerade ekvationen fås nu genom att multiplicera ekvationen med multiplikativa inversen:  [3] [5]  [x] = [3] [2]. Men [3] [5] =[1], så detta ger  [1]  [x] = [6], så [x] = [6] är lösningen till den reducerade ekvationen.


5. Lösningen till ekvationen fås nu av Sats B5.10, nämligen

[x] = [6 + t(7)] där t=0, 1, så
lösningen är [x] = [6] eller [13] i Z₁₄.  

Exempel (Viktigt!)
Bestäm alla lösningar x  till kongruensen  10x  4  (mod 14).
 

Lösning:
Kongruensen motsvaras av ekvationen [10]  [x] = [4] i Z₁₄, så av exemplet ovan fås att lösningen är alla heltal i de två kongruensklasserna [6] och [13] i Z₁₄. Dvs. att kongruensen har lösningarn

x = 14k+6 eller 14k+13 = 7k+6, där k .

Uppgift B5.10
(a) Bestäm alla lösningar i  Z₁₂ till ekvationen  [10]  [x] = [6].
(b) Bestäm alla lösningar  x  till kongruensen  10x  6  (mod 12).
 

Uppgift B5.11
(a) Bestäm den multiplikativa inversen till  [14]  i Z₃₇.
(b) Bestäm x₀ med  0  x₀ 36  och  14x₀ 1 (mod  37).
(c) Bestäm alla heltalslösningar  x  till kongruenserna
        (i)  42x  15 (mod  111);
       (ii)  42x   25 (mod  111).
 
 

6. Förslag till övningsuppgifter

Uppgifterna i texten ovan.

Övningsuppgifter från [EG] kapitel 3:

3.32, 3.33, 3.34, 3.35,
3.45, 3.46, 3.47, 3.48, 3.49, 3.50,
3.58.

Week Exercise 6

Uppgift

(a) Bestäm den multiplikativa inversen till  [1261]  i Z₁₆₂₁.
     Tips: Använd uppgift 1(b) på veckouppgift 5.

(b) Bestäm x₀ med  0  x₀ 1620  och  1261x₀ 1 (mod  1621).

(c) Bestäm alla lösningar [x] i  Z₁₆₂₁ till ekvationen  [1261]  [x] = [3].

(d) Bestäm alla heltalslösningar  x  till kongruenserna
        (i)  1261x  3 (mod  1621);
       (ii)  1261x  5 (mod  1621).