Följder och summor

Referenser

[EG]   avsnitt 4.1;
och nedanstående text.

Nyckelord

Rekursion, talföjder, rekursiva definitioner, summanotation, produktnotation.

Inledning

I detta block skall vi först lära oss den grundläggande terminologin för ändliga, oändliga talföljder. Sedan skall vi lära oss att uttrycka stora summeringar och produkt på ett kompakt sätt.

1. Följder

Börja med att läsa inledningen till avsnitt 4.1 i [EG] kursivt. Det handlar om rekursion, grundbegreppet i detta block.

Läs då delavsnitt 4.1.1 i [EG] fram till exempel 4.7 sida 77. Här definieras talföljder.

En oändlig/ändlig följd är en oändlig/ändlig ordnad lista av symboler (som regel tal), där varje element i listan har ett nummer, som vi kallar elementets index. En generell oändlig följd har inget sista element och ser därför ut som:

där varje s_n, n=1, 2, 3, ... , är en symbol. En ändlig följd har ett sista element och är därför på formen

där 1 är följdens första index och t är följdens sista index.

Observera, att en oändlig följd

kan anges på flera olika sätt. T.ex. används på denna kurs följande tre:

1. "låt s vara en följd";
2. "låt {s_n} vara en följd";
3. "låt {s_n} 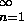vara en följd".

Notationerna under punkt 2. och 3. används i [EG], men är en aning osedvanliga. Det är mer vanligt att skriva (s_n) och (s_n)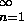 i stället för {s_n} och {s_n}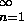 . Grunden till detta är, at parenteserna { och } används för att markera mängder, som vi såg i block 3, och följder är inte mängder. Mängder är oordnade samlingar av objekt, medan en av de mest karakteristiska egenskaperna hos en följd är, att den är ordnad.

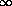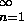Övre indexet i {s_n } utläses som "oändlig" och används för att indikera, att följden inte har något sista index och därför inte något sista element. Undre indexet n=1 i {s_n}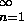 används för att ange att följdens första index är 1, och följdens första element är därför s₁. Om följden är ändlig och har s_t som sista element, anger man i övre indexet följdens sista index, t, i stället för 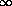. På samma sätt är det ibland klokt att låta en följds första index vara ett annat nummer än 1, t.ex. 0, och i sådana fall anger man detta genom att låta undre indexet vara "n=0" i stället för "n=1", d.v.s.

{s_n}.

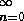2. Rekursiva definitioner

Vad du bör kunna göra när du är klar med  avsnitt [EG] 4.1 är att bestämma en rekursionsformel  från några regler som i exempel 4.5 sidan 74-75.

På sida 73 hittar vi definitionen på en rekursionsformel för en talföljd. Observera att för att bestämma en talföljd,  är det inte tillräkligt med bara en rekursionsformel. Man behöver också startvillkoren.

På sida 75 ges definitionen av Fibonacciföljden.  Observera att det finns olika sätt att definiera denna.

3. Sigmanotation för summor

Det är ofta nödvändigt att skriva summan av alla element från en ändlig följd. Betrakta till exempel följden s bestående av de 25 första jämna positiva heltalen:

dvs. s_n = 2n for n=1, 2, 3, ... , 25.
Summan av alla element i denna följd är

Detta långa uttryck är det omöjligt att skriva mer än ett par gånger i en text, och tänk på hur det skulle ha sett ut om vi hade valt att betrakta summan av de 250 första jämna heltalen i stället för de första 25! Vi inför därför ett nytt och kompakt sätt att skriva sådana summor på. Den nya metoden kallas summanotation eller sigmanotation, och ovanstående summa S skrivs

Denna kompakta notation skall tolkas på följande sätt: För varje heltal n mellan 1 och 25, beräkna och skriv värdena av uttrycket 2n och sätt in ett "+" - tecken mellan alla värden.

Generellt skriver vi summan av alla elementen i följden (u_n)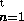 som

Tecknet är en grekisk bokstav, som motsvarar bokstaven S i det latinska alfabetet, och står för summa. Hela uttrycket utläses som "summan av u_n från n=1 till n=t", och tolkas på följande sätt: För varje heltal n mellan 1 och t, beräkna och skriv värdet av u_n och sätt ett "+" - tecken mellan alla värden.

Betrakta till exempel summan

Först beräknar vi värdena (3n-1) för n=1, 2, 3, 4:

och så sätter vi "+"-tecken emellan alla dessa värden:

Vi har därför

Sats B2.1.
Följande två räkneregler gäller för vår nya notation:

cun = c

un,

(un+vn) =

un +

vn

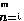där   (un) och   (vn)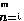 är ändliga följder av tal och c är en konstant.

Bevis.
Dessa räkneregler följer lätt av de kända räknereglerna för 'allmänna' summor:

	cun	=	cui+cui+1+cui+2 + ... +cum
		=	c(ui+ui+1+ui+2+ ... +u m)
		=	c( u n)
		=	c un .

	(un+vn)	=	(ui+vi)+(ui+1+vi+1) + ... +(um+vm)
		=	(ui+ui+1+ ... +um) + (vi +vi+1+ ... +vm) (som ses genom att flytta om element i summan)
		=	un + vn.

Läs nu om summa- och produktnotation i [EG] delavsnitt 4.1.2 (4.1.2.1 kursivt) och 4.1.3.

4. Förslag till övningsuppgifter

Övningsuppgifter från [EG] kapitel 4:

4.1, 4.3, 4.4
4.5, 4.6, 4.9, 4.10, 4.11(a)
4.15, 4.16, 4.35, 4.37, 4.38
4.39, 4.40, 4.41, 4.42, 4.43, 4.44.

Week Exercise 7

Click here to download the week exercise which is in pdf-format only!