Grafer II
Referenser
[EG] avsnitt 6.4, 6.5, 6.6 (ej 6.6.1);
och nedanstående text.
Nyckelord
Mer terminologi för grafer, grannmatris, incidensmatris. Grafisomorfier. Träd, minimala spännande träd, Kruskal's algoritm. Rotade träd, bredden-först sökning och djupet-först sökning. Binära sökträd.
Inledning
I detta block skall vi se närmare på grafer. Vi skall först lära oss om när grafer är lika: grafisomorfier. Största delan av blocket handlar dock om en speciell slags grafer som kallas träd.
1. Grannmatrisen och incidensmatrisen för en graf
Vi har redan sett att en graf kan representeras med en ritning eller med
en lista med hörn och en lista med kanter.
I [EG] avsnitt 6.4 kommer ett par
andra metoder. Den första är grannmatrisen för en graf och
den andra är incidensmatrisen.
2. Grafisomorfier
Läs [EG] avsnitt 6.4.
Idéen bakom begreppet grafisomorfi är inte alltför svår men att faktiskt avgöra om två grafer är isomorfa är inte alltid en så enkel uppgift. Vad menar vi med isomorfi av grafer? Vi menar att två grafer representerar samma situation även om de tycks ha olika utseende.
Exempel
Följande två grafer
kan båda representera 5 personer, där en person, i den första
grafen a och i den andra grafen 3, känner 4 andra personer, och att
e känner både b och a motsvarar i den andra grafen 1 som känner
3 och 2.
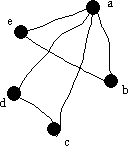
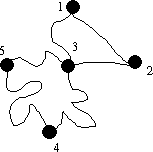
Vi kan para ihop varje hörn i den första grafen med ett hörn i den andra grafen, så att kanterna i den första grafen motsvaras av kanterna i den andra grafen. Ett sätt på vilket detta kan göras är med bijektiva funktionen
 3, b
3, b 2, c
2, c 4, d
4, d 5,
e
5,
e 1.
1.En snabb kontroll visar att alla kanterna i den första grafen motsvaras av kanter i den andra grafen. Om du kan para ihop hörn på detta sätt, så att även kanterna tas med, så är graferna isomorfa (isomorphic). Om det är omöjligt att göra detta så är graferna inte isomorfa.
För att visa att två grafer är isomorfa så måste du lyckas para ihop hörnen. För att visa att två grafer inte är isomorfa så kan du visa på någon skillnad mellan graferna, som t.ex.:
- olika antal hörn
- olika antal kanter
- olika antal cykler av längd 3
- olika hörnvalens
- Om båda graferna är enkla kan det ibland vara lättare
att undersöka vilka kanter som inte finns med, ty två grafer är isomorfa
om och endast om deras komplementer är isomorfa. (Komplementet till en graf G
innehåller alla
kanter
som inte finns med i G tillsammans med alla hörn i G.) Denna metod är speciellt
användbar när graferna innehåller många kanter, vilket
innebär att komplementgraferna har få kanter.
Exempel
Här är ett exempel på en graf och dess komplement.
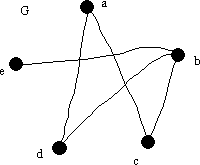
Grafen 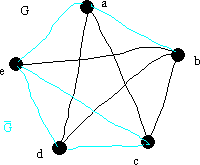
Grafen och dess komplement 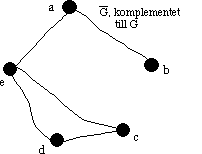
Komplementet
3. Träd
Som vi sa tidigare har vi alla stött på träd förut i form av familjeträd, utslagsturneringar och filsystemet hos datorer. Träd används också när man optimerar sökmetoder och när man analyserar antalet beslut man behöver göra i en valsituation. Vi hinner tyvärr inte titta på alla den här typen av problem i den här kursen.
Introduktion
 Träd
kan användas när man analyserar RNA, för
att ta reda på släktskapet mellan olika växter, skalbaggar,
virus och så vidare. Detta är ett område inom matematisk
biologi. Om du är intresserad av att läsa mer om detta kan du titta
på nätet på sidan
The Tree of Life .
Träd
kan användas när man analyserar RNA, för
att ta reda på släktskapet mellan olika växter, skalbaggar,
virus och så vidare. Detta är ett område inom matematisk
biologi. Om du är intresserad av att läsa mer om detta kan du titta
på nätet på sidan
The Tree of Life .
Vi har nu nämt ett antal användningsområden för träd, men vad är ett träd för någonting? Ett träd (tree) är en graf som är sammanhängande och saknar cykler. En graf som består av komponenter som alla är träd kallas för, ja vadå, tänk ut ett bra namn för en samling träd.
|
Du har troligtvis gissat rätt, men |
 Vissa träd
har ett speciellt hörn som valts som rot (root). Dessa träd kallas för
rotade träd (rooted trees), och av någon anledning brukar man rita dem med roten
uppåt som i bilden till vänster. Om vi fortsätter med naturkunskapen,
så har rotade träd grenar (branches) och löv (leaves). Dessa begrepp
introduceras i avsnitt
6.6 i [EG].
Vissa träd
har ett speciellt hörn som valts som rot (root). Dessa träd kallas för
rotade träd (rooted trees), och av någon anledning brukar man rita dem med roten
uppåt som i bilden till vänster. Om vi fortsätter med naturkunskapen,
så har rotade träd grenar (branches) och löv (leaves). Dessa begrepp
introduceras i avsnitt
6.6 i [EG].
Ett annat sätt att använda träd är i problem av följande typ. Tänk igenom vilka krav en bra lösning skall uppfylla först innan du läser delavsnitt 6.5.1 i [EG].
Bredbandsproblemet
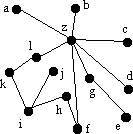 Antag att det har beslutats att alla i Sverige skall ha bredband, och att
man lägger ner minsta antalet kablar som behövs. Diagrammet till
vänster visar den föreslagna planen för att lägga kablarna.
Är det en bra plan? Går det att reducera antalet kablar? Om det
går, hur? Om inte, varför?
Antag att det har beslutats att alla i Sverige skall ha bredband, och att
man lägger ner minsta antalet kablar som behövs. Diagrammet till
vänster visar den föreslagna planen för att lägga kablarna.
Är det en bra plan? Går det att reducera antalet kablar? Om det
går, hur? Om inte, varför?
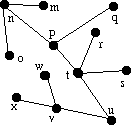 För en anna
del av landet, har förslaget till vänster valts. Går det
att reducera antalet kablar i det här fallet? Om det går, hur?
Om inte, varför?
För en anna
del av landet, har förslaget till vänster valts. Går det
att reducera antalet kablar i det här fallet? Om det går, hur?
Om inte, varför?
Betrakta båda exemplen, vilken typ av graf löser problemet? Tänk igenom detta en stund, och kontrollera sedan svaret i avsnittet om spännande träd nedan.
Viktade bredbandsproblemet
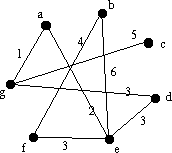 Antag att vi också vet kostnaden för varje kabel, såsom
visas i grafen till höger. Talet som finns vid varje kant representerar
kostnaden för den kabeln. Hur skalll man ta reda på vilka kablar
man skall lägga för att minimera kostnaden? Fundera ut ett sätt
som du tycker fungerar för grafen till vänster. I avsnittet om
minimala spännande träd nedan finns det en algoritm
för att lösa
den här typen av problem.
Antag att vi också vet kostnaden för varje kabel, såsom
visas i grafen till höger. Talet som finns vid varje kant representerar
kostnaden för den kabeln. Hur skalll man ta reda på vilka kablar
man skall lägga för att minimera kostnaden? Fundera ut ett sätt
som du tycker fungerar för grafen till vänster. I avsnittet om
minimala spännande träd nedan finns det en algoritm
för att lösa
den här typen av problem.
Definitioner och terminologi för träd
Läs [EG] Avsnitt 6.5 t.o.m. sidan 161.
Återigen måste vi vara försiktiga med definitionerna. Vad som menas med ett 'träd' är standard, men man kan ge definitionen på flera sätt. Definitionen i avsnitt 6.5 i [EG] är:
- Ett träd är en sammanhängande graf utan cykler.
- Ett träd T är en enkel graf som uppfyller att, om v och w är hörn i T, så finns en unik stig från v till w.
Är de två definitionerna ekvivalenta?
Att det inte finns några cykler innebär att det inte finns några
loopar eller parallella kanter (Varför?).
Definitionen av sammanhängande
säger att det finns åtminstone en
stig från v till w. 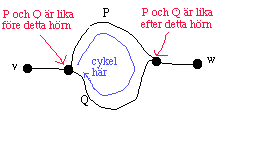 Vi skall visa att om en graf inte innehåller några cykler, så
kan det inte finnas mer än en stig mellan varje par av hörn. Vi
gör detta genom att se vad som händer om det finns två
stigar P och Q mellan ett par av hörn som vi kallar v och w. Vi ser
i diagrammet till vänster att det ger en cykel. Detta visar att det
är omöjligt att inte få cykler i en graf som har två
stigar mellan ett par av hörn. Vi har kommit fram till att om
det inte finns några cykler i en graf så medför det att
det finns högst en stig mellan varje par av hörn. Så
båda definitionerna betyder samma sak.
Vi skall visa att om en graf inte innehåller några cykler, så
kan det inte finnas mer än en stig mellan varje par av hörn. Vi
gör detta genom att se vad som händer om det finns två
stigar P och Q mellan ett par av hörn som vi kallar v och w. Vi ser
i diagrammet till vänster att det ger en cykel. Detta visar att det
är omöjligt att inte få cykler i en graf som har två
stigar mellan ett par av hörn. Vi har kommit fram till att om
det inte finns några cykler i en graf så medför det att
det finns högst en stig mellan varje par av hörn. Så
båda definitionerna betyder samma sak.
När du har läst sidorna 160 - 161 i [EG], skall du
- veta att ett träd har (antalet hörn - 1) kanter.
Spännande träd
Läs [EG] Avsnitt 6.5 sidan 162.
 STOPP! Tänk igenom de två förslagen i
bredbandsproblemet ovan innan du läser vidare.
STOPP! Tänk igenom de två förslagen i
bredbandsproblemet ovan innan du läser vidare.
I det första förslaget ser vi att det finns en cykel
Vi kan ta bort vilken kant som hellst från cykeln utan att dela grafen i bitar. Detta betyder att det finns åtminstone en kant för mycket i det första förslaget. I allmänhet vill vi ju inte ha några cykler i vårt förslag och vi vill att grafen skall vara sammanhängande. Det är samma sak som att säga att vi letar efter ett träd som innehåller alla hörn i grafen. Ett sådant träd kallas för ett (upp)spännande träd (spanning tree).
I det andra förslaget har vi redan ett träd. Om vi tar bort en kant kommer inte grafen längre att vara sammanhängande, vilket betyder att ett träd är det bästa resultatet. Hur många kablar behövs? Exakt antalet kanter i trädet, som är samma antal som antalet hörn minus 1. (Observera: Om vi tar bort en kant från ett träd, så blir resultatet en skog bestående av två träd.)
Finns det alltid en lösning till den här typen av problem? Ja, så länge som grafen man utgår ifrån är sammanhängande. Hur hittar man ett uppspännande träd? Svaret hittar du i avsnittet om Bredden-först- och Djupet-först sökning nedan.
4. Minsta uppspännande träd
Läs [EG] Delavsnitt 6.5.1.
 STOPP! Tänk igenom den viktade versionen av
bredbandsproblemet ovan innan du läser vidare.
STOPP! Tänk igenom den viktade versionen av
bredbandsproblemet ovan innan du läser vidare.
Precis som förrut vill vi hitta ett uppspännande träd. I det här fallet vill vi dessutom ha det till minsta möjliga kostnad. Ett sådant träd kallas för ett minsta (eller minimalt) (upp)spännande träd. Det finns en metod i delavsnitt 6.5.1 för att lösa detta problem: Kruskals algoritm. Här finns ett exempel av algoritm för bredbandsproblemet:
Kruskals Algoritm
Exempel:
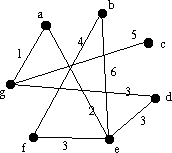 |
Vi söker reda på kanten med minsta vikten och lägger till den till en mängd E. Kant ag har lägst vikt så E={ag}. Vi färgar kanten ag röd. |
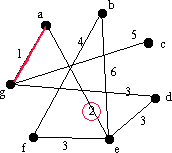 |
Nu letar vi reda på den kant med lägst vikt som finns i den svarta delen av grafen. Det finns en kant av vikt 2 och det är ae. Vi kollar så att ae inte bildar en cykel med någon av kanterna i E. Det gör den inte så vi lägger till ae till E, så E={ag, ae} |
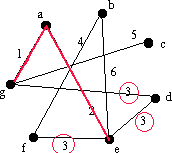 |
Nu letar vi reda på nästa kant med lägst vikt. Det finns tre kanter av vikt 3, gd, ed och ef. Vi väljer en, t.ex. gd, och kollar så att det inte bildas några cykler med kanter i E. Det gör det inte, så vi lägger till kanten till E. Nu är E={ag, ae, gd}. |
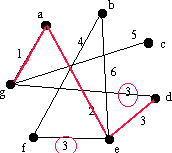 |
Nu kollar vi en annan kant av längd 3 nämligen ed. Denna bildar en cykel med kanterna i E nämligen aedga. Eftersom vi vill ha ett träd, lägger vi inte till den här kanten, utan tar bort den från grafen. |
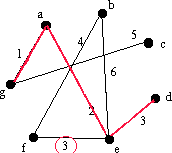 |
Den sista kanten av vikt 3 är ef, och den ger ingen cykel så vi lägger till den till E, så att vi får E={ag, ae, gd, ef}. |
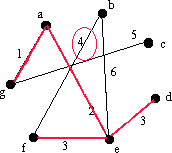 |
Vi lägger till bf till E. |
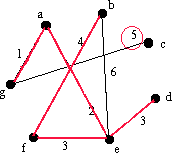 |
Vi lägger till gc till E. |
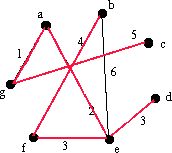 |
Nu har vi 6 kanter i E och G har 7 hörn. Eftersom vi vet att ett träd har (antal hörn - 1) kanter, har vi rätt antal kanter för ett träd. Vi har hittat ett minsta uppspännande träd. Det har sina kanter i E och sina hörn i G. |
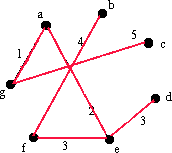 |
Ett minsta uppspännande träd av vikt 18. |
När du har läst delavsnitt 6.5.1 i [EG], skall du
- veta vad följande termer betyder: mininimalt (upp)spännande träd (minimum spanning tree),
- kunna utföra Kruskals algoritm,
- kunna beskriva Kruskals algoritm.
Rotade träd
Läs nu delavsnitt 6.5.2 och avsnitt 6.6 t.o.m. sidan 168 i [EG]. De handlar om rotade träd.Två definitioner som dyker upp är definitionerna av höjd (height) och nivå (level) i ett rotat träd. Höjden av ett träd är den maximala längden av en stig som startar i roten. Nivån hos ett hörn är avståndet (antalet kanter) mellan hörnet och roten.
Då du har läst delavsnitt 6.5.2 och avsnitt 6.6 i [EG] skall du veta vad följande saker betyder: träd, höjd, ett hörns nivå, rotat träd, föräldrar, barn, och löv. Binärt sökträd, balanserat binärt sökträd.Bredden-först- och Djupet-först sökning
I delavsnitt 6.5.2 finns två metoder att hitta ett uppspännande träd. Båda startar vid ett valt hörn (roten). Följande diagram och tabeller ger ett exempel på hur dessa metoder fungerar.
Betrakta grafen:
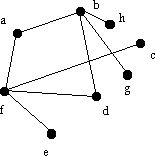
I båda
metoder startar vi sökningen vid hörn a.
| Bredd före djup-sökning | |||||||
| Lista över hörnen | Söker vid | Lägg till hörn till lista | Ta bort hörn från lista | Lägg till kant till träd | Trädet så långt | Sökväg så långt | Kommentarer |
| a | a | f | - | af | 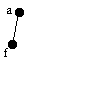 |
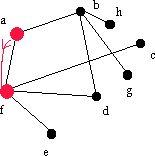 |
Lägg till f till slutet på listan. Leta alltid efter grannar till det första hörnet i listan. I det här fallet, leta efter grannar till a och fortsätt tills det inte finns några kvar. |
| af | a | b | - | ab | 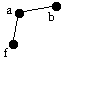 |
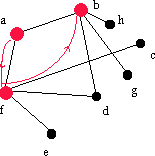 |
Fortsätter att söka efter grannar till a. |
| afb | a | - | a | - | - | - | Det finns inga fler grannar till a så vi tar bort a från listan, och fortsätter att söka vid nästa hörn i listan. |
| fb | f | e | - | fe | 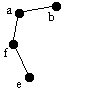 |
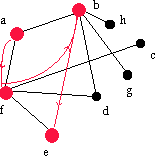 |
Söker efter grannar till f. |
| fbe | f | d | - | fd | 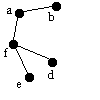 |
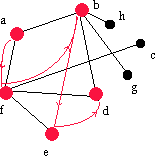 |
Söker efter grannar till f. |
| fbed | f | c | - | fc | 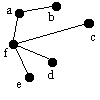 |
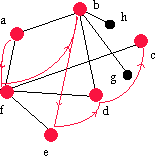 |
Söker efter grannar till f. |
| fbedc | f | - | f | - | - | - | Det finns inga fler grannar till f, så vi tar bort det från listan. |
| bedc | b | g | - | bg | 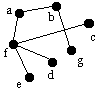 |
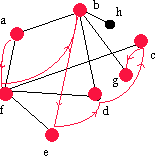 |
Söker efter grannar till b. |
| bedcg | b | h | - | bh | 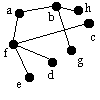 |
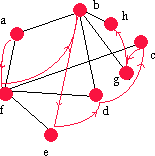 |
Nu har vi undersökt alla hörn i grafen och vi kan avsluta sökningen. |
I en del fall kan det hända att listan med hörn blir tom innan man undersökt alla hörn. Detta betyder att grafen måste vara icke-sammanhängande, den består alltså av mer än en komponent. I sådana fall hittar man ett uppspännande träd för varje komponent, dessa utgör då en uppspännande skog för grafen.
| Djup före bredd-sökning | |||||||
| Lista över hörnen | Söker vid | Lägg till hörn till lista | Ta bort hörn från lista | Lägg till kant till träd | Trädet så långt | Sökväg så långt | Kommentarer |
| a | a | f | - | af | 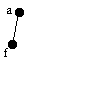 |
 |
Återigen lägger vi till f till listan. Med den här metoden söker vi vid det sista hörnet i listan så vi fortsätter att söka vid f. |
| af | f | e | - | fe | 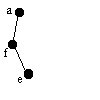 |
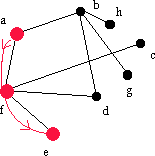 |
Vi söker efter en granne till f, som vi lägger till i listan. |
| afe | e | - | e | - | - | 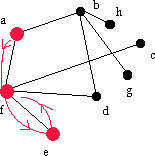 |
Vi söker efter en granne till e, men det finns ingen, så ta bort e från listan och gå tillbaka till f för nästa steg. |
| af | f | d | - | fd | 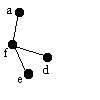 |
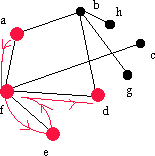 |
Vi söker efter en ny granne till f och hittar d. |
| afd | d | b | - | db | 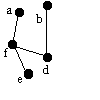 |
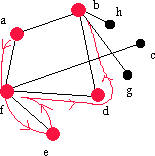 |
Vi söker vid d och hittar b. |
| afdb | b | g | - | bg | 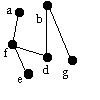 |
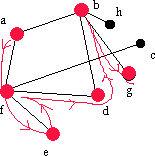 |
Vi söker vid b och hittar g. |
| afdbg | g | - | g | - | - | 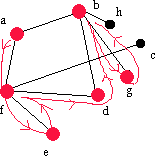 |
Vi söker vid g och hittar inga nya grannar, så vi går tillbaka till b igen för nästa steg. |
| afdb | b | h | - | bh | 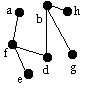 |
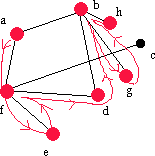 |
Vi söker vid b och hittar h. |
| afdbh | h | - | h | - | - | 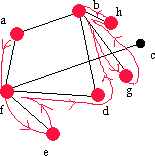 |
Det finns inga nya grannar vid h, så vi går tillbaka till b igen. |
| afdb | b | - | b | - | - | 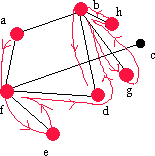 |
Det finns inga nya grannar till b, så vi går tillbaka till d. |
| afd | d | - | d | - | - | 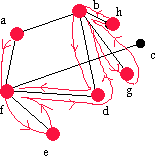 |
Det finns inga nya grannar till d, så vi går tillbaka till f. |
| af | f | c | - | fc | 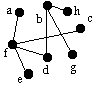 |
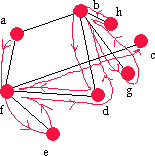 |
Antingen kan vi stanna här eftersom alla hörn finns med i trädet, eller så fortsätter man tills listan är tom. |
När du har läst delavsnitt 6.5.2 i [EG], skall du också kunna
- vad följande termer betyder: (upp)spännande träd (spanning tree)
- hur man genomför en bredden-först sökning
- hur man genomför en djupet-först sökning
6. Övningsuppgifter
Övningsuppgifter från [EG] kapitel 6:
6.42, 6.43, 6.44, 6.46, 6.47, 6.48, 6.49, 6.50, 6.51, 6.52;
6.53, 6.55, 6.56, 6.58, 6.59, 6.61, 6.62, 6.63, 6.54;
6.65, 6.67, 6.68;
6.69, 6.70, 6.71, 6.72, 6.73, 6.74;
6.76, 6.77, 6.78, 6.79, 6.80, 6.81, 6.82.
6.92, 6.93, 6.94, 6.95, 6.96, 6.97, 6.98 (ej in-, pre- och postordning),
6.99 (ej in-, pre- och postordning),
Week Exercise 9
Please click here to download week exercise 9 in pdf-format.This is the 2nd Edition of the study guide for Block 9 of Discrete Mathematics for the Vocational
Study Programme in Information Technology, written by
Pia Heidtmann in 2006.
The study guide may be printed for personal use by
anybody with an interest.
This study guide and any parts of it and any previous and future versions of it must not
be copied or disseminated in any printed or electronic form
or stored on any publicly accessible website other than
http://www.tfm.miun.se/~piahei/dmy/res/
without permission from the author.
The author welcomes comments and corrections via email.
All contributions incorporated in updates of the manuscript will be acknowledged.
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
