Interaktiv Matematik
Komplexa tal
Division, z1/z2 - lång version
(Det finns också en kortare version om du vill ha mindre förklaringar eller bakgrund.)
När man dividerar komplexa tal med varandra klarar man sig inte längre med samma
räkneregler som vanligt, de säger ju inget om hur man dividerar med i, och om i vet vi
inget mer än att i× i = -1, dvs inget om division. Det
finns dock ett bra knep att ta till som alltid fungerar. Det bygger på det faktum att
produkten av ett komplext tal och dess konjugat (zz*) alltid är ett reellt tal,
och dividera med reella tal kan vi. Att (zz*) alltid är ett reellt tal beskrivs i
ett eget avsnitt, liksom multiplikation i allmänhet. Har du inte läst dessa avsnitt
innan, så gör det nu. Knepet består därför i att förlänga bråket med nämnarens
konjugat. Då blir nämnaren alltid reell, och vi kan utföra en "vanlig"
division. Om vi har två komplexa tal, z1 = a+bi och z2 = c+di, beräknar vi
deras kvot så här: 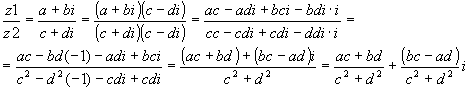
Notera hur vi förlänger bråket med nämnarens konjugat, multiplicerar ihop parenteserna som vanligt, ersätter i× i med –1, och sedan grupperar termerna så att vi får de reella för sig och de imaginära för sig. Vi ser alltså att det vid division med komplexa tal inte finns ett lika lätt samband för real- och imaginärdelarna som vid addition och subtraktion. Dock finns det, som vi snart skall se, ett samband mellan belopp och argument, precis som vid multiplikation av komplexa tal.
Här bredvid ser du ett exempel på division av komplexa tal. Talen kallas som ovan z1 och z2, och är betecknade med en röd respektive en blå punkt. Det går också en röd resp. en blå linje från origo ut till punkterna. Här är inte real- och imaginärdelarna till talen utmärkta, eftersom det inte finns något enkelt samband att visa. Kvoten z1/z2 är betecknad med en grön punkt och linje. I figuren visas geometriskt hur divisionen fungerar.
Du kan nu ta tag i de båda komplexa talen z1 och z2 med musen och släpa runt dem i det komplexa talplanet. Du ser då hur kvoten hänger med och förändras. Släpa nu runt z1 och z2 till olika ställen, och se till att du får en bild av hur divisionen fungerar. Efter en stund kan du gärna försöka förutse vad som kommer att hända innan du gör en förändring.
Här kanske du noterar något annat om hur divisionen fungerar. Om du är uppmärksam kan du se att beloppet av z1/z2 är lika med kvoten av beloppen för z1 och z2. Du kan också se att argumentet av z1/z2 är lika med differensen av argumenten för z1 och z2. Detta betecknas så här: |z1/z2| = |z1|/|z2|, respektive arg(z1/z2) = arg(z1) - arg(z2). Du kan se detta så här: om du förlänger/förkortar pilen till z1 (utan att vrida den), så förlängs/förkortas pilen för z1/z2 än mer utan att vridas, om du förlänger/förkortar pilen till z2 (utan att vrida den), så förkortas/ förlängs pilen för z1/z2 än mer utan att vridas (alltså tvärtom mot för z1), och om du vrider pilen till något av talen z1 eller z2 (utan att förlänga eller förkorta dem), så vrids pilen för z1z2 med utan att förlängas eller förkortas. Oroa dig inte om du inte förstår detta nu, det kommer att gås igenom mer senare i kursen. Återvänd gärna hit då.
Prova nu gärna att själv räkna på detta med papper och penna, genom att hitta på några komplexa tal, beräkna deras kvot, och pricka in dem i det komplexa talplanet. Genomför divisionen både genom att räkna teoretiskt med real- och imaginärdelarna, och genom att dividera belopp och subtrahera argument.
Tillbaka till Komplexa tal.
© Per Edström, TNV, Mitthögskolan.
Uppdaterad: 1999-06-07