
Logik
1. Introduktion till logik
Varför skulle vi vilja studera logik? Det kan vara för att det hjälper oss att förstå ett problem och dra slutsatser. Det hjälper oss att skriva klartext så att missförstånd inte uppstår. Det ger en bra bas för matematik och datalogi. Det ger oss möjlighet att skriva om ett påstående så att det nya påståendet är sant precis när det ursprungliga påståendet är sant. Allt detta hjälper oss att lösa problem, bevisa satser och skriva dataprogram. Dessa anteckningar är bara en kort introduktion till ämnet. Om du vill läsa mer om detta viktiga och nödvändiga ämne så kan du läsa kursen Introduktion till logik A (5 poäng).
Följande exempel är övningar i logiskt tänkande. Vilken information är
given? Vilken information är relevant? Vilka slutsatser kan du dra från
den? Finns det ett sätt att skriva om problemet så att det blir lättare att
förstå och lösa? Dessa frågor uppstår ofta när man försöker lösa ett
problem.
1.1. 1 poäng eller 0 poäng?
På en skola deltog 100 elever i ett spel. Varje elev fick 1 eller 0 poäng. Minst en av eleverna fick 0 poäng, men för varje valfritt par elever var summan av deras poäng minst 1.
 Finns det tillräckligt
med information för att bestämma hur många av eleverna som fick 1 poäng?
Vad tycker du?
Finns det tillräckligt
med information för att bestämma hur många av eleverna som fick 1 poäng?
Vad tycker du?
1.2. Jörgens bilder
Jörgen tittade på ett foto. Jag frågade honom vem fotot föreställde. Han svarade, som han brukar göra, i kryptisk stil: ''Jag har inga syskon, men denne mans far är min fars son!''
 Suck! Nu är jag förvirrad. Vem är det på bilden? Vet du?
Suck! Nu är jag förvirrad. Vem är det på bilden? Vet du?
 Naturligtvis, när jag inte kunde lösa hans gåta, skrattade han och visade
mig ett foto till. Som en galen frågade jag vem det var. Han svarade:
''Jag har inga syskon, men denne mans son är min fars son.'' Åh! Hjälp!
Naturligtvis, när jag inte kunde lösa hans gåta, skrattade han och visade
mig ett foto till. Som en galen frågade jag vem det var. Han svarade:
''Jag har inga syskon, men denne mans son är min fars son.'' Åh! Hjälp!
1.3. Gåtrike
Varje år reser Jörgen till gåtrike för att njuta av deras hemska gåtor. Sista gången hade han en underbar upplevelse. Han fick chans att titta på när regeringen kom till följande beslut, som de naturligtvis gav ut i form av en gåta. I regeringen är det bara fem medlemmar och de röstade i fem frågor.
i. Ska gåtskolan vara obligatorisk?
ii. Ska alla glasspaket ha en gåta så att man måste lösa gåtan innan man
kan äta glassen?
iii. Ska varje medborgare ge en gåta som avgift till staten varje månad?
iv. Ska den som ''inte tänker, bara gör'' få minst 25 års fängelse och
rehabilitering?
v. Ska utlänningar få ett visum om de inte kan lösa rikets pussel?
Deras röster kan man bestämma från följande påståenden:
a. Totala antalet ''ja''-röster var ett större än totala antalet
''nej''-röster.
b. C röstade aldrig ''nej'' i två på varandra följande frågor?
c. A, B och E röstade på samma sätt i den andra frågan.
d. D röstade ''ja'' i den fjärde frågan.
e. C och E röstade olika i de första tre frågorna, dvs. om C röstade ''ja''
så röstade E ''nej'', eller tvärtom.
f. Det fanns inte två frågor som hade samma antal ''ja''-röster.
g. Fråga 3 fick en ''ja''-röst mer än fråga 2.
 Vad var deras beslut och vem röstade ''ja'' i vilka frågor? Hur kom du
till din slutsats?
Vad var deras beslut och vem röstade ''ja'' i vilka frågor? Hur kom du
till din slutsats?
2. Påståenden, logikens byggstenar
När vi försöker lösa ett problem är det ofta viktigt att dela upp det i mindre delar som är lättare att förstå och jobba med. Har du löst problemet med Jörgens bild? Om du betraktar "denne mans far är min fars son" kan man skriva om det till "denne mans far är jag" som är lättare att hantera. Både "denne mans far är min fars son" och "denne mans far är jag" är exempel på påståenden. Men vad är ett påstående? Det är en mening som är antingen sann eller falsk och inte är en åsikt. Sanningsvärdet av ett påstående är "sant" om det är sant och "falskt" om det är falskt.
Följande är några exempel på påståenden.
 Sundsvall ligger i Spanien.
Sundsvall ligger i Spanien.
 Det finns liv på Mars.
Det finns liv på Mars.
 Sarah tycker att surströmming smakar bra.
Sarah tycker att surströmming smakar bra.
 x > 5
x > 5
Följande är inte påståenden.
 Smakrik mat
Smakrik mat
 Vilket väder!
Vilket väder!
 35
35
 2/5
2/5
 Detta påstående är falskt.
Detta påstående är falskt.
 Matematik är intressant
Matematik är intressant
 Det vita huset
Det vita huset
Kanske undrar du varför "Sarah tycker att surströmming smakar bra" är ett påstående? Det är för att "Sarah tycker att surströmming smakar bra" är sant eller falskt. Åsikten "Matematik är intressant" är inte ett påstående.
Ett annat sätt att tänke på påståenden är om du frågade din dator "Är detta sant", så kunde den svara, given att den hade tillräckligt information. Är 2/5 sant? Det har ingen betydelse. Din dator blir inte glad om du frågade det! Om du frågade "Är 'Sarah tycker att surströmming smakar bra' sant?" så kunde den svara.
2.1. Övning
Vilka av följande är påståenden?
1. Sundsvall ligger i Sverige.
2. 762 + 43 + 21/2
3. x = 3
4. Det kommer att regna den 21 juni 2020.
5. Detta påstående är falskt.
2.2. Negation
Betrakta påståendet "Snön är grön." Är det sant? Nej, det är falskt. "Snön
är inte grön" är sant. "Snön är inte grön" är negationen av "Snön är grön."
Vad är negationen av ett påstående?
2.2.1. Definition*: negation
Negationen av ett påstående p är ett påstående som är falskt precis när p är sant och sant precis när p är falskt.
(*OBS! Definitioner är viktiga. Varför? I matematiken är det ofta
så att ord inte betyder samma sak som i det vanliga språket. Definitioner
hjälper oss att vara överens om precis vad ett ord betyder.)
2.2.2. Exempel
Negationen av "Lena är kvinna" är "Lena är inte kvinna" eller "Lena är
man".
Negationen av "x > 5" är "x ≤ 5".
Negationen av "Jon är 75 år gammal" är "Jon är inte 75 år gammal".
2.2.3. Övning
 Lösningar till denna övning kan du hitta på webbsajten.
Lösningar till denna övning kan du hitta på webbsajten.
Bestäm negationen av följande påståenden.
1. Mia är längre än 2,00 m.
2. Fredrik har brunt hår.
3. Heltalet x är udda.
4. Sarah är engelska och Pia är danska.
Har du bestämt negationen i övning 2.2.3.4? Det var inte så lätt, eller hur? Ett problem kan vara att vi inte vet exakt vad "och" betyder. I nästa avsnitt pratar vi om "och" och "eller".
2.3. Och, eller
Alla påståenden som vi har pratat om är ganska korta och enkla. I vanlig svenska pratar vi inte bara i korta meningar utan vi använder ord som länkar meningar tillsammans, t.ex. "och", "eller", "men". Det kan vara svårt att veta exakt vad någon verkligen säger, t.ex. "Det är inte Sarah och Pia." Betyder det att "det är inte Sarah och det är inte Pia," eller betyder det negationen av "Det är Sarah och Pia," dvs. att "det är inte både Sarah och Pia"? En dator måste veta precis vad vi menar, så vi ger en exakt definition av "och " och "eller".
2.3.1. Definition av ''och''
Låt p och q vara två påståenden. Påståendet "p och q" är sant endast när både p och q är sanna, och falskt när minst ett av p och q är falskt.
2.3.2. Exempel
Sveriges drottning heter Silvia och statsministern heter Kalle Anka. Detta är falskt eftersom trots att drottningen verkligen heter Silvia, heter inte statsministern Kalle Anka.
2.3.3. Definition av ''eller''
Låt p och q vara två påståenden. Påståendet "p eller q" är sant när minst ett av p och q är sant, och falskt när både p och q är falska.
2.3.4. Exempel
Sveriges drottning heter Silvia eller statsministern heter Kalle Anka. Detta är sant eftersom drottningen heter Silvia, så det spelar ingen roll vad statsministern heter — vi har redan att minst ett av påståendena är sant så det hela är också sant.
2.3.5. Övningar
 Lassie
Lassie
 Nalle Puh
Nalle Puh
Bestäm vilka av följande påståenden som är sanna och vilka som är falska.
1. Nalle Puh är en hund och det snöar aldrig i Sverige.
2. Nalle Puh är en hund eller det snöar aldrig i Sverige.
3. Nalle Puh är en hund eller det snöar ibland i Sverige.
4. Lassie är en hund och det snöar ibland i Sverige.
5. Lassie är en hund eller det snöar ibland i Sverige.
6. 30 > 5 och 1 + 4 = 7
7. 30 > 5 eller 1 + 4 = 7
2.3.6. Övningar
 Lösningar till denna övning kan du hitta på webbsajten.
Lösningar till denna övning kan du hitta på webbsajten.
Låt p vara påståendet "5 < 3", låt q vara påståendet "En vecka
innehåller precis 6 dagar", och låt r vara påståendet "Alla hästar är
bruna". Bestäm om följande påståenden är sanna eller falska.
(a) (p och q) eller (icke r)
(b) (p eller q) och r
(c) (p eller q) och (p och r)
2.4. Sanningstabeller
Låt p och q vara påståenden. Är "p och (q och icke p)" sant eller falskt? Beror det på p och q eller bara ett av dem? Låt oss betrakta alla möjliga fall: (1) p är sant och q är falskt, (2) p är sant och q är sant, (3) p är falskt och q är sant, (4) p är falskt och q är falskt. I fall 1 har vi 'sant och (sant och falskt)'. Vi vet att 'A och B' är sant endast om både A och B är sant, dvs. 'sant och falskt' är därför falskt, så vi har 'sant och falskt' som är falskt. Det var lite svårt att förstå, eller hur? Det är lite lättare att se vad som händer om vi använder en s.k. sanningstabell. Vi skriver en etta om påståendet som står högst upp i kolonnen är "sant" och en nolla om det är "falskt".
| p | q | icke p | q och icke p | p och (q och icke p) |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Är det en överraskning att p och (q och icke p) alltid är falskt? Kanske, men inte om vi tänker efter lite grann. Varför? Först, "p och q" är samma sak som "q och p". Vidare är "p och (q och icke p)" samma som "(p och q) och icke p". Detta betyder att vi får ta bort parentesen och ändra ordning på "p", "q" och "icke p", precis som med multiplikation av tal. Vi vet att "A och B" är sant när både A och B är sant. Är det möjligt för "p" och "icke p" att vara sant samtidigt? Nej! Varför? Definitionen av "icke p" säger att "p" och "icke p" har motsatta sanningsvärden. Ett påstående som alltid är falskt kallas för en motsägelse (eller kontradiktion), och ett som alltid är sant kallas för en tautologi.
2.4.1. Några regler om "och" och "eller"
Ovan, träffade vi på några regler för "och". Vi summerar dem, och några
till, här.
1. "p och (q och r)" är samma som "(p och q) och r". [Jämför med
multiplikation av heltal: a(bc) = (ab)c.]
2. "p eller (q eller r)" är samma som "(p eller q) eller r". [Jämför med
addition av heltal:
a + (b + c) = (a + b) + c.]
3. "p och q" är samma som "q och p". [För heltal: ab = ba.]
4. "p eller q" är samma som "q eller p". [För heltal:
a + b = b + a.]
2.4.2. Övningar
 Lösningar till denna övning kan du hitta på webbsajten.
Lösningar till denna övning kan du hitta på webbsajten.
1.Skriv sanningstabeller för
(a) p och q
(b) icke p
(c) p eller q
(d) (p och q) eller r [Ledning: Det finns 8 möjliga kombinationer av
sant/falskt för p, q och r.]
(e) (p eller r) och (q eller r)
2. Jämför dina svar till (d) och (e).
2.4.3. p och (q eller r)
Med addition och multiplikation av heltal, kan vi skriva om (a + b)c som
ac + bc. Vi kan göra samma sak med påståenden, om vi byter "plus" mot
"eller", och "gånger" mot "och"! Det betyder att "(p eller q) och r" är
ekvivalent med "(p och r) eller (q och r)". Ett ögonblick! Vad betyder
"ekvivalent"? Det betyder att båda påståendena har precis samma
sanningsvärde, dvs. båda påståendena betyder samma
sak men uttrycker det på olika sätt. Där vi har skrivit "är samma som" i 2.4.1 borde vi har skrivit
"är ekvivalent med" eller använt pilen 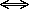 .
Vi skriver om dem och några till.
.
Vi skriver om dem och några till.
1. "p och (q och r)" 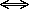 "(p och q) och
r".
"(p och q) och
r".
2. "p eller (q eller r)" 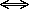 "(p eller q)
eller r".
"(p eller q)
eller r".
3. "p och q"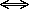 "q och p".
"q och p".
4. "p eller q" 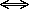 "q eller p".
"q eller p".
5. "(p eller q) och r" 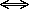 "(p och r) eller
(q och r)".
"(p och r) eller
(q och r)".
6. "(p och q) eller r" 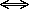 "(p eller r) och
(q eller r)".
"(p eller r) och
(q eller r)".
1 och 2 kallas för associativa lagar, 3 och 4 för kommutiva lagar, och 5 och
6 för distributionslagar.
2.4.4. Exempel
Vi försöker att skriva "(p och q) eller icke p" på ett så enkelt sätt som
möjligt genom att använda reglerna 1 – 6. Med hjälp
av distributionslagarna ser vi att '(p och q) eller icke p' 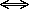 '(p eller icke p) och (q eller icke
p)'. Vi vet att för att "A och B" ska vara sant måste både A och B
vara sanna. "p eller icke p" är alltid sant, så '(p eller icke p) och
(q eller icke p)' är sant om och endast om 'q eller icke p' är sant,
dvs. sanningsvärdet hos hela påståendet beror endast på 'q eller icke
p'.
'(p eller icke p) och (q eller icke
p)'. Vi vet att för att "A och B" ska vara sant måste både A och B
vara sanna. "p eller icke p" är alltid sant, så '(p eller icke p) och
(q eller icke p)' är sant om och endast om 'q eller icke p' är sant,
dvs. sanningsvärdet hos hela påståendet beror endast på 'q eller icke
p'.
2.4.5. Övningar
 Lösningar till denna övning kan du hitta på webbsajten.
Lösningar till denna övning kan du hitta på webbsajten.
Skriv följande på så enkelt sätt som möjligt med hjälp av reglarna ovan
och definitionerna av "och" och "eller". Om ett påstående är en tautologi,
skriv att det är ekvivalent med T, en allmän tautologi. Om det är
ekvivalent med en motsägelse, skriv att det är ekvivalent med M, en allmän
motsägelse. Kontrollera med hjälp av sanningstabeller, att dina svar är
ekvivalenta med de ursprungliga påståendena.
(a) (p eller q) och (q eller p)
(b) (p och q) och q
(c) (p eller q) och p
(d) (p eller q) och (p och r),
(e) (icke p eller p) eller q,
(f) (icke p) och (p och q),
(g) (icke p och p) eller q,
2.5. Negationen av "och", "eller"
Jag hoppas att du har gjort övning 2.2.3 del 4. Om du inte har gjort den, gör den nu. Det frågas om negationen av ett påstående i formen "p och q". Vi ser att negationen är (icke p) eller (icke q). Kontrollera, med hjälp av en sanningstabell, att det stämmer. Hur tror du att vi kan skriva om icke (p eller q)? Det är samma idé som med icke (p och q). Vi byter "och" mot "eller", och "multiplicerar ut". Det ger oss två nya regler.
7. icke (p och q) 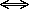 (icke p) eller (icke
q).
(icke p) eller (icke
q).
8. icke(p eller q) 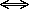 (icke p) och (icke
q).
(icke p) och (icke
q).
Lagarna 7 och 8 kallas för de Morgans lagar.
2.5.1. Exempel
Vi förenklar icke(icke (p och q) eller icke q).
| icke(icke (p och q) eller icke q) | 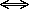 |
(p och q) och q | [de Morgans lagar, och "icke icke p" är samma som "p"] |
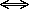 |
p och (q och q) | [associativa lagarna] | |
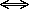 |
p och q. | [definition av "och"] |
2.5.2. Övningar
 Lösningar till denna övning kan du hitta på webbsajten.
Lösningar till denna övning kan du hitta på webbsajten.
Förenkla följande påståenden. Förklara vilka lagar som du använder i varje
steg. Kontrollera dina svar med hjälp av sanningstabeller. (OBS! När vi
skriver "icke p och q" menar vi "(icke p) och q", dvs. vi utför operationen
"icke" först.)
(a) icke(icke (p eller q) och icke q)
(b) icke(p och q) eller p
(c) icke(p eller q) och p
(d) icke((icke p och icke q) och icke r)
2.6. Implikation
Ofta säger vi någonting som "om ... så ...", t.ex. "om du köper en t-shirt, så får du en till gratis." Denna typ av påstående är ganska vanlig inom programmering och inom matematik. Det kan vara lite svårt att förstå när det är sant och när det är falskt. Vi ska betrakta de fyra olika fallen, men först skriver vi om uttrycket som "om p så q" där p är "du köper en t-shirt" och q är "du får en t-shirt gratis.
Fall 1: p och q är sanna. Det betyder att "om p så q" också är sant.
Fall 2: p är sant och q är falskt. Då blir du inte glad! Affären har ljugit
för dig. Påståendet är falskt!
Fall 3: p är falskt och q är sant. Vad glad du blir! Du får en t-shirt utan
att köpa en. Kanske har du köpt någonting annat, men det spelar ingen roll,
affären har inte ljugit. Påståendet är sant.
Fall 4: p är falskt och q är falskt. Du köper ingen t-shirt. Du får ingen
t-shirt gratis. Affären har inte ljugit för dig. Påståendet är sant.
Med detta exempel som grund, kan vi, med hjälp av en sanningtabell, definiera "om p så q". Observera att "om p så q" är falskt endast när p är sant och q är falskt. När p är falskt spelar det ingen roll om q är sant eller ej.
| p | q | om p så q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ett annat sätt att se på det hela är att tänka på följande if-sats.
if( x < 0 ) { return "x är positivt"; }
När kommer du att upptäcka felet? Om x < 0 är falskt, dvs. x ≥ 0, kommer
satsen inte att köras, så det spelar ingen roll vad det står inom satsen. Men
om x < 0 är sant, så körs satsen
och du får veta att x är positivt, vilket det inte är, så du upptäckar felet! Problemet uppstår
endast när x < 0 är sant och "x är positivt" är falskt. Det
betyder att när vi vill kolla om "om p så q" är sant, så behöver vi endast
kolla vad som händer när p är sant. Om det leder till att q är falskt, så är
påståendet falskt. Om det leder till att q är sant, så är
påståendet sant.
2.6.1. Övningar
Bestäm om eller när följande påståenden är sanna eller falska genom att
betrakta om fallet "p är sant" och "q är falskt" uppstår.
1. Om grisar kan flyga så är Kalle Anka Sveriges kung.
2. Om x > 4 så är x2 < 10.
3. Om Sveriges drottning heter Silvia, så kan grisar flyga.
2.6.2. "Om ... så ..." på andra former
Det finns många sätt att uttrycka "om p så q" t.ex.
- Om p gäller så gäller q.
- Om p är sant, så är q sant.
- p är ett tillräckligt villkor för q.
- p gäller endast om q gäller.
- p medför q.
- p
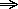 q
q
- p implicerar q
- q är ett nödvändigt villkor för p.
2.6.3. Skyldig eller icke skyldig?
I en värld långt långt bort, där öron är spetsiga och logiken regerar utspann sig följande konversation.

 Varför var det inte det bästa för mannen att säga?
Varför var det inte det bästa för mannen att säga?
2.6.4. Övningar
 Lösningar till denna övning kan du hitta på webbsajten.
Lösningar till denna övning kan du hitta på webbsajten.
Ge sanningstabeller för
(a) (icke q) 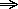 (icke p)
(icke p)
(b) p 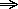 q
q
(c) icke (p och icke q)
Jämför dina svar på (a) – (c).
2.6.5. Vanliga fel
Första felet
Ett vanligt fel är att läsa "om p så q" och tänka "om q så p." Dessa
påståenden är inte ekvivalenta!
Betrakta följande två påståenden, som är sanna.
(i) Om jag är gift så gillar min man inte spindlar.
(ii) Min man gillar inte spindlar om jag gillar dem.
Vi kan inte dra slutsatsen att jag gillar spindlar! Det är som en
enkelriktad gata — man får inte köra i fel riktning.
Ett annat vanligt fel i samma stil är att när man får en sann slutsats så kan man tro att det ursprungliga påståendet också var sant. Ett exempel är följande. Observera att alla steg är korrekta!
Vi visar att 0 = 1. (Eek!)
0 = 1 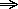 1×0 = 0×0
1×0 = 0×0 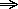 0 = 0
0 = 0
(Och här kommer felet...) Eftersom 0 = 0 är sant så är även
0 = 1 sant.
Om du tittar i sanningstabellen för p 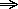 q, ser du att om p
q, ser du att om p 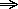 q är sant, så kan p vara sant eller falskt när q är sant — vi vet inte
vilket fall vi har. Men om slutsaten q är falsk, så vet vi att p också är
falskt. Ett exempel är följande.
q är sant, så kan p vara sant eller falskt när q är sant — vi vet inte
vilket fall vi har. Men om slutsaten q är falsk, så vet vi att p också är
falskt. Ett exempel är följande.
0 = 1 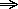 1 + 1 = 0 + 1
1 + 1 = 0 + 1 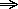 2 = 1. Eftersom 2 ≠ 1 är
2 = 1 falskt, så därför är 0 = 1 också falskt.
2 = 1. Eftersom 2 ≠ 1 är
2 = 1 falskt, så därför är 0 = 1 också falskt.
Andra felet
Ett annat fel är att skriva någonting som "meaning of life 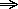 42". Vad är det för fel? Felet är att
"meaning of life" och "42" inte är påståenden. Du skulle nog inte skriva
någonting sånt, men kanske du kan tänka dig att skriva 2x = 6
42". Vad är det för fel? Felet är att
"meaning of life" och "42" inte är påståenden. Du skulle nog inte skriva
någonting sånt, men kanske du kan tänka dig att skriva 2x = 6 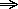 3. Jag blir jätte
3. Jag blir jätte  om du gör det!
om du gör det!
2.6.6. Övningar
I vilka av följande uppgifter är symbolen 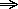 rätt använd?
rätt använd?
(a) x – 2 = 5 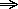 7
7
(b) x – 2 = 5 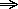 – 7
– 7
(c) 0 = 1 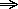 0 + 0 = 1 + 0
0 + 0 = 1 + 0
(d) x – 2 = 5 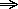 x = 7
x = 7
2.7. Ekvivalenta påståenden
Vi har redan pratat lite grann om ekvivalenta påståenden: två påståenden p
och q är ekvivalenta om de alltid har samma sanningsvärde. Vi skriver
detta som "p 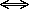 q". Pilen
q". Pilen 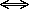 ser ut som en kombination av
ser ut som en kombination av 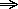 och
och 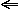 , och det är precis vad den är, dvs. p
, och det är precis vad den är, dvs. p 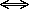 q är ekvivalent med (p
q är ekvivalent med (p 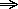 q) och (p
q) och (p 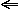 q)! Vi använder en sanningstabell för att visa att detta
stämmer.
q)! Vi använder en sanningstabell för att visa att detta
stämmer.
| p | q | p 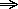 q q |
p 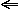 q q |
p 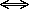 q q |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
2.7.1. Andra sätt att uttrycka ekvivalens
Istället för att säga p är ekvivalent med q kan vi säga:
p är liktydigt med q
p gäller om och endast om q gäller
p omm q [förkortning av ''om och endast om'']
p iff q [förkortning av engelskans ''if and only if'']
p är ett nödvändigt och tillräckligt villkor för q
p och q är antingen båda sanna eller båda falska.
2.7.2. Övningar
Vilka av följande påstående är sanna?
(a) 0 = 1 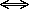 0 × 0 = 1 × 0.
0 × 0 = 1 × 0.
(b) x – 2 = 5 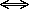 x = 3.
x = 3.
(c) x = 2 och x² = 4 är antingen båda sanna eller
båda falska.
2.8. Alla, Inget, Något
Ofta pratar vi om "alla" t.ex. "Alla tycker om surströmming". Är det sant? Nej, t.ex. min man tycker inte om surströmming. Så "Alla tycker om surströmming" är falskt, men om det är falskt, vad har det för negation? Är det "Ingen tycker om surströmming"? Det kan inte vara det för att jag tycker om surströmming så "Ingen tycker om surströmming" är falskt också. Negationen av "Alla tycker om surströmming" måste vara "Någon tycker inte om surströmming". Negationen av "Ingen tycker om surströmming" är "Någon tycker om surströmming".
I det allmäna fallet är negationen av "För alla x, q", där q är ett påstående, "Det existerar x: icke q". I exemplet ovan står x för "person" och q för "person tycker om surströmming".
Negationen av "Det existerar x: q" är "För alla x: icke q". Negationen av "För alla x: q" är "Det existerar x: icke q".
2.8.1. Övning
 Lösningar till denna övning kan du hitta på webbsajten.
Lösningar till denna övning kan du hitta på webbsajten.
Bestäm om följande påståenden är sanna eller falska, och skriv ner deras
negation.
1. Det finns ett heltal större än 3.
2. Alla positiva heltal är större eller lika med 1.
3. Alla jämna tal är delbara med 4.
4. För varje heltal x finns det ett heltal y så att x > y.
c/o Pia Heidtmann
MID SWEDEN UNIVERSITY
Department of Engineering, Physics and Mathematics
Mid Sweden University
S-851 70 SUNDSVALL
Sweden
This note and any parts of it and any previous and future versions of it must not
be copied or disseminated in any printed or electronic form
or stored on any publicly accessible website other than
http://www.tfm.miun.se/~piahei/dmy/res/
without permission from Pia Heidtmann.
The author welcomes comments and corrections via email.
All contributions incorporated in updates of the manuscript will be acknowledged.
The author would like to thank the following for their contribution
to various updates of the original manuscript:
Sam Lodin, Fredrik Ståhl, Mikael Torenfält and Pia Heidtmann.