Interaktiv Matematik

Vektorer, punkter och linjer i 2 dimensioner

Avstånd mellan punkter - lång version
(Det finns också en kortare version om du vill ha mindre förklaringar eller bakgrund.)

Nu när vi kan beräkna vektorn mellan två punkter och normen (längden) av en vektor, är det lätt att beräkna avståndet mellan två punkter. Först beräknar man vektorn mellan punkterna, och sedan beräknar man längden av den. Det är avståndet mellan punkterna.

Om vi nu har två punkter P(Px, Py) och Q(Qx, Qy), så vi tidigare sett att att PQ = (Qx-Px, Qy-Py). Längden av PQ får vi med Pythagoras sats: 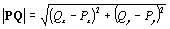, vilket alltså är avståndet mellan punkterna P och Q.
///////////////////////////////////// // Fixed coordinate system ///////////////////////////////////// // Origin for X-Y-coordinate system // X-axis // Y-axis ///////////////////////////////////// // The "application" ///////////////////////////////////// // Real numbers' axis ///////////////////////////////////// // Arrowheads /////////////////////////////////////

Här bredvid ser du ett exempel på detta. Punkterna kallas som ovan P och Q, och är betecknade med en blå respektive röd punkt. Mellan dem är vektorn PQ utritad som en lila pil, och på tallinjen undertill i figuren är avståndet mellan punkterna markerat med l, och utritad med en lila punkt och ett lila streck.

Du kan nu ta tag i punkterna P och Q med musen och förändra dem. Du ser då hur vektorn PQ och avståndet l hänger med och förändras. Flytta nu runt punkterna, och se till att du får en bild av hur detta fungerar.

Prova nu gärna att själv räkna på detta med papper och penna, genom att hitta på några punkter, beräkna avståndet mellan dem, och pricka in dem i koordinatsystemet. Genomför detta både genom att använda Pythagoras sats, och genom att mäta pilar.

Tillbaka till Vektorer, punkter och linjer i 2 dimensioner.
© Per Edström, TNV, Mitthögskolan.
Uppdaterad: 1999-07-01