Interaktiv Matematik
Vektorer, punkter och linjer i 2 dimensioner
Enhetsvektor - lång version
(Det finns också en kortare version om du vill ha mindre förklaringar eller bakgrund.)
En enhetsvektor är en vektor med normen ett. Ofta talar man om enhetsvektorn i en viss riktning, eller enhetsvektorn till en annan vektor. Man menar då en vektor med samma riktning som den ursprungliga vektorn, men med normen ett. Man säger ibland att man normerar en vektor, vilket innebär att man förändrar dess längd så att den blir ett, men riktingen förblir oförändrad. Som för alla vektorer har dock placeringen ingen betydelse. Ofta kallas enhetsvektorer e med ett index efter sin ursprungliga vektor. För vektorn v har vi alltså enhetsvektorn ev.
Eftersom vi kan beräkna normen för en vektor, kan vi nu ganska enkelt beräkna enhetsvektorn till en vektor. Vi känner ju till att om man multiplicerar en vektor med en skalär så ändras vektorns längd men inte dess riktning. Om vi nu multiplicerar vektorn med skalären 1/|v|, så får vi ju en vektor med samma riktning, men med längden ett, dvs enhetsvektorn.
Om vi nu har en vektor v = (x, y), så är dess norm ![]() .
Således gäller att
.
Således gäller att 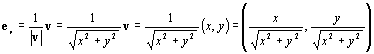 .
.
Här bredvid ser du ett exempel på detta. Vektorn kallas som ovan v, och är betecknad med en röd pil. Dess enhetsvektor ev är betecknad med en blå pil, och är utritad på två ställen, dels med början där v börjar, dels med början i origo.
Du kan nu ta tag i vektorn v med musen och förändra den. Du ser då hur enhetsvektorn hänger med och förändras. Flytta nu runt vektorn, och se till att du får en bild av vad enhetsvektorn innebär.
Prova nu gärna att själv räkna på detta med papper och penna, genom att hitta på några vektorer, beräkna enhetsvektorn för dem, och pricka in dem i koordinatsystemet. Genomför detta både genom att använda Pythagoras sats, och genom att förlänga/förkorta pilar.
Tillbaka till Vektorer, punkter och linjer i 2 dimensioner.
© Per Edström, TNV, Mitthögskolan.
Uppdaterad: 1999-07-01